[toc]

方向导数

如果函数 z=f(x,y) 在点 P(x,y) 是可微分的, 那么, 函数在该点沿任一方向 L 的方向导数都存在, 且有:

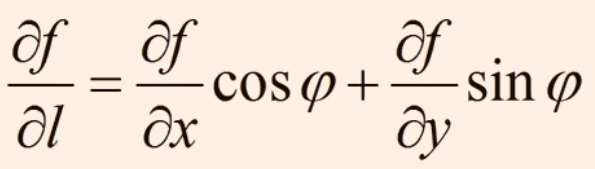
梯度

设函数 z=f(x,y) 在平面区域 D 内具有一阶连续偏导数, 则对于每一个点 P(x,y)∈D, 向量

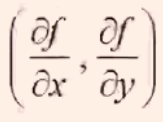
为函数 z=f(x,y) 在点 P 的梯度, 记做 grandf(x,y)

梯度的方向是函数在该点变化最快的方向

• 考虑一座解析式为 z=H(x,y) 的山, 在(N0,y0) 的梯度是在该点坡度变化最快的方向.

坡度下降法

文章来源: iamarookie.blog.csdn.net，作者：我是小白呀，版权归原作者所有，如需转载，请联系作者。

原文链接：iamarookie.blog.csdn.net/article/details/109740392