Python 统计基础：(一)如何描述您的数据

目录

在大数据和人工智能时代，数据科学和机器学习已经成为许多科技领域必不可少的。处理数据的一个必要方面是能够直观地描述、总结和表示数据。Python 统计库是全面、流行且广泛使用的工具，可帮助您处理数据。

在本教程中，您将学习：

• 您可以使用哪些数字量来描述和总结您的数据集
• 如何在纯 Python 中计算描述性统计量
• 如何使用可用的 Python 库获取描述性统计信息
• 如何可视化您的数据集

了解描述性统计

描述性统计是关于描述和总结数据。它使用两种主要方法：

1. 定量方法以数字方式描述和总结数据。
2. 可视化方法使用图表、绘图、直方图和其他图形来说明数据。

您可以将描述性统计应用于一个或多个数据集或变量。当您描述和总结单个变量时，您正在执行单变量分析。当您搜索一对变量之间的统计关系时，您正在进行双变量分析。同样，多变量分析同时涉及多个变量。

选择 Python 统计库

有许多 Python 统计库可供您使用，但在本教程中，您将了解一些最流行和广泛使用的库：

• Python'sstatistics是一个用于描述性统计的内置 Python 库。如果您的数据集不太大或者您不能依赖导入其他库，则可以使用它。

• NumPy是用于数值计算的第三方库，针对处理一维和多维数组进行了优化。它的主要类型是称为 的数组类型ndarray。该库包含许多用于统计分析的例程。

• SciPy是基于 NumPy 的第三方科学计算库。与 NumPy 相比，它提供了额外的功能，包括scipy.stats统计分析。

• Pandas是基于 NumPy 的第三方数值计算库。它擅长处理带有Series对象的标记一维 (1D) 数据和带有对象的二维 (2D) 数据DataFrame。

• Matplotlib是一个用于数据可视化的第三方库。它与 NumPy、SciPy 和 Pandas 结合使用效果很好。

请注意，在许多情况下，可以使用Series和DataFrame对象代替 NumPy 数组。通常，您可能只是将它们传递给 NumPy 或SciPy统计函数。此外，您可以通过调用or 来从 aSeries或DataFrame作为np.ndarray对象获取未标记的数据。.values.to_numpy()

Python 统计库入门

内置的 Pythonstatistics库具有相对较少的最重要的统计函数。该官方文档是寻找细节的宝贵资源。如果您仅限于使用纯 Python，那么 Pythonstatistics库可能是正确的选择。

开始学习 NumPy 的好地方是官方用户指南，尤其是快速入门和基础部分。该官员引用可以帮你刷新具体NumPy的概念，你的记忆。在阅读本教程时，您可能还想查看统计部分和官方scipy.stats参考资料。

如果您想学习 Pandas，那么官方入门页面是一个很好的起点。在介绍数据结构可以帮助你了解基本数据类型，Series以及DataFrame。同样，优秀的官方介绍性教程旨在为您提供足够的信息，让您开始在实践中有效地使用 Pandas。

matplotlib有一个全面的官方用户指南，您可以使用它来深入了解使用该库的详细信息。Matplotlib 剖析对于想要开始使用matplotlib及其相关库的初学者来说是一个很好的资源。

让我们开始使用这些 Python 统计库！

计算描述性统计量

首先导入您需要的所有包：

>>> import math
>>> import statistics
>>> import numpy as np
>>> import scipy.stats
>>> import pandas as pd

这些是 Python 统计计算所需的所有包。通常，您不会使用 Python 的内置math包，但它在本教程中会很有用。稍后，您将导入matplotlib.pyplot以进行数据可视化。

让我们创建一些数据来处理。您将从包含一些任意数字数据的 Python 列表开始：

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> x_with_nan = [8.0, 1, 2.5, math.nan, 4, 28.0]
>>> x
[8.0, 1, 2.5, 4, 28.0]
>>> x_with_nan
[8.0, 1, 2.5, nan, 4, 28.0]

现在您有了列表x和x_with_nan. 它们几乎相同，不同之处在于x_with_nan包含一个nan值。了解 Python 统计例程在遇到非数字值 ( nan)时的行为非常重要。在数据科学中，缺失值很常见，您经常将它们替换为nan.

>>> math.isnan(np.nan), np.isnan(math.nan)
(True, True)
>>> math.isnan(y_with_nan[3]), np.isnan(y_with_nan[3])
(True, True)

现在，创建对应于and 的np.ndarrayandpd.Series对象：xx_with_nan

>>> y, y_with_nan = np.array(x), np.array(x_with_nan)
>>> z, z_with_nan = pd.Series(x), pd.Series(x_with_nan)
>>> y
array([ 8. ,  1. ,  2.5, 4. , 28. ])
>>> y_with_nan
array([ 8. ,  1. ,  2.5,  nan,  4. , 28. ])
>>> z
0     8.0
1     1.0
2     2.5
3     4.0
4    28.0
dtype: float64
>>> z_with_nan
0     8.0
1     1.0
2     2.5
3     NaN
4     4.0
5    28.0
dtype: float64

您现在有两个 NumPy 数组（y和y_with_nan）和两个 Pandas Series（z和z_with_nan）。所有这些都是一维值序列。

您可以选择指定的每个值的标签z和z_with_nan。

中央倾向的措施

集中趋势的度量显示数据集的中心值或中间值。对于数据集的中心，有多种定义。在本教程中，您将学习如何识别和计算这些集中趋势的度量：

• 意思
• 加权平均数
• 几何平均数
• 谐波平均值
• 中位数
• 模式

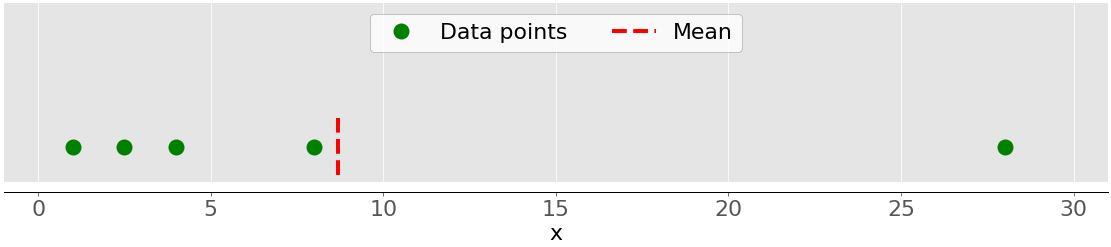
绿点代表数据点 1、2.5、4、8 和 28。红色虚线是它们的平均值，或 (1 + 2.5 + 4 + 8 + 28) / 5 = 8.7。

您可以使用sum()和使用纯 Python 计算平均值len()，而无需导入库：

>>> mean_ = sum(x) / len(x)
>>> mean_
8.7

虽然这很干净优雅，但您也可以应用内置的 Python 统计函数：

>>> mean_ = statistics.mean(x)
>>> mean_
8.7
>>> mean_ = statistics.fmean(x)
>>> mean_
8.7

您已经从内置 Python库中调用了函数mean()和函数，并获得了与使用纯 Python 相同的结果。在Python 3.8 中引入作为. 它总是返回一个浮点数。fmean()statisticsfmean()mean()

但是，如果nan您的数据中有值，则statistics.mean()和statistics.fmean()将nan作为输出返回：

>>> mean_ = statistics.mean(x_with_nan)
>>> mean_
nan
>>> mean_ = statistics.fmean(x_with_nan)
>>> mean_
nan

此结果与 的行为一致sum()，因为sum(x_with_nan)也返回nan。

如果您使用 NumPy，那么您可以通过以下方式获得平均值np.mean()：

>>> mean_ = np.mean(y)
>>> mean_
8.7

在上面的例子中，mean()是一个函数，但你也可以使用相应的方法.mean()：

>>> mean_ = y.mean()
>>> mean_
8.7

NumPy的函数mean()和方法.mean()返回与statistics.mean(). 当nan您的数据中有值时，情况也是如此：

>>> np.mean(y_with_nan)
nan
>>> y_with_nan.mean()
nan

您通常不需要因此获得nan值。如果您更喜欢忽略nan值，则可以使用np.nanmean()：

>>> np.nanmean(y_with_nan)
8.7

nanmean()只是忽略所有nan值。它返回的值与mean()您将其应用于没有nan值的数据集相同。

pd.Series对象也有方法.mean()：

>>> mean_ = z.mean()
>>> mean_
8.7

如您所见，它的使用方式与 NumPy 的情况类似。但是，.mean()Pandasnan默认忽略值：

>>> z_with_nan.mean()
8.7

这种行为是可选参数的默认值的结果skipna。您可以更改此参数以修改行为。

加权平均数

该加权平均，也称为加权算术平均法或加权平均，是算术平均值，使您可以定义每个数据点到结果的相对贡献的推广。

您为数据集 𝑥 的每个数据点 𝑥ᵢ定义一个权重 𝑤ᵢ，其中 𝑖 = 1、2、……、𝑛 和 𝑛 是 𝑥 中的项目数。然后，您将每个数据点与相应的权重相乘，对所有乘积求和，并将获得的总和除以权重的总和：Σᵢ(𝑤ᵢ𝑥ᵢ) / Σᵢ𝑤ᵢ。

当您需要包含以给定相对频率出现的项目的数据集的平均值时，加权平均值非常方便。例如，假设您有一个集合，其中所有项目的 20% 等于 2，50% 的项目等于 4，其余 30% 的项目等于 8。您可以计算平均值这样的一套：

>>> 0.2 * 2 + 0.5 * 4 + 0.3 * 8
4.8

在这里，您将频率与权重一起考虑在内。使用此方法，您无需知道项目总数。

您可以通过sum()与range()或结合使用纯 Python 实现加权平均值zip()：

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> w = [0.1, 0.2, 0.3, 0.25, 0.15]
>>> wmean = sum(w[i] * x[i] for i in range(len(x))) / sum(w)
>>> wmean
6.95
>>> wmean = sum(x_ * w_ for (x_, w_) in zip(x, w)) / sum(w)
>>> wmean
6.95

同样，这是一个干净优雅的实现，您不需要导入任何库。

但是，如果您有大型数据集，那么 NumPy 可能会提供更好的解决方案。您可以使用np.average()来获取 NumPy 数组或 Pandas 的加权平均值Series：

>>> y, z, w = np.array(x), pd.Series(x), np.array(w)
>>> wmean = np.average(y, weights=w)
>>> wmean
6.95
>>> wmean = np.average(z, weights=w)
>>> wmean
6.95

结果与纯 Python 实现的情况相同。您也可以在普通列表和元组上使用此方法。

另一种解决方案是使用元素之积w * y与np.sum()或.sum()：

>>> (w * y).sum() / w.sum()
6.95

就是这样！您已经计算了加权平均值。

但是，如果您的数据集包含nan值，请小心：

>>> w = np.array([0.1, 0.2, 0.3, 0.0, 0.2, 0.1])
>>> (w * y_with_nan).sum() / w.sum()
nan
>>> np.average(y_with_nan, weights=w)
nan
>>> np.average(z_with_nan, weights=w)
nan

在这种情况下，average()返回nan，这与 一致np.mean()。

谐波平均值

的调和平均是倒数平均数据集中的所有项目的倒数的：𝑛/Σᵢ（1 /𝑥ᵢ），其中𝑖= 1，2，...，𝑛和𝑛是在数据集中𝑥项目的数量。调和平均值的纯 Python 实现的一种变体是：

>>> hmean = len(x) / sum(1 / item for item in x)
>>> hmean
2.7613412228796843

它与x您计算为 8.7的相同数据的算术平均值完全不同。

您还可以使用以下方法计算此度量statistics.harmonic_mean()：

>>> hmean = statistics.harmonic_mean(x)
>>> hmean
2.7613412228796843

上面的示例显示了statistics.harmonic_mean(). 如果您nan在数据集中有一个值，那么它会返回nan. 如果至少有一个0，那么它会返回0。如果您提供至少一个负数，那么您将得到statistics.StatisticsError：

>>> statistics.harmonic_mean(x_with_nan)
nan
>>> statistics.harmonic_mean([1, 0, 2])
0
>>> statistics.harmonic_mean([1, 2, -2])  # Raises StatisticsError

使用此方法时，请记住这三个场景！

计算调和平均值的第三种方法是使用scipy.stats.hmean()：

>>> scipy.stats.hmean(y)
2.7613412228796843
>>> scipy.stats.hmean(z)
2.7613412228796843

同样，这是一个非常简单的实现。但是，如果您的数据集包含nan、0、负数或除正数之外的任何内容，那么您将得到一个ValueError!

几何平均数

的几何平均值是所有𝑛元素的乘积的𝑛次方根𝑥ᵢ在数据集中𝑥：ⁿ√（Πᵢ𝑥ᵢ），其中𝑖= 1,2，...，𝑛。下图说明了数据集的算术、调和和几何平均值：

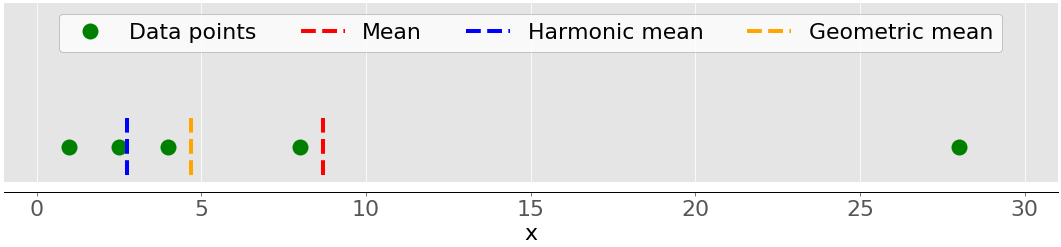
同样，绿点代表数据点 1、2.5、4、8 和 28。红色虚线是平均值。蓝色虚线是调和平均值，黄色虚线是几何平均值。

您可以像这样在纯 Python 中实现几何平均值：

>>> gmean = 1
>>> for item in x:
...     gmean *= item
...
>>> gmean **= 1 / len(x)
>>> gmean
4.677885674856041

如您所见，在这种情况下，几何平均值的值与同一数据集的算术平均值 (8.7) 和调和平均值 (2.76) 的值有显着差异x。

Python 3.8 引入了statistics.geometric_mean()，它将所有值转换为浮点数并返回它们的几何平均值：

>>> gmean = statistics.geometric_mean(x)
>>> gmean
4.67788567485604

您得到了与上一个示例相同的结果，但舍入误差最小。

如果您传递带有nan值的数据，statistics.geometric_mean()则将像大多数类似的函数一样运行并返回nan：

>>> gmean = statistics.geometric_mean(x_with_nan)
>>> gmean
nan

事实上，这与行为一致statistics.mean()，statistics.fmean()和statistics.harmonic_mean()。如果您的数据中有零或负数，statistics.geometric_mean()则将提高statistics.StatisticsError.

您还可以使用以下方法获得几何平均值scipy.stats.gmean()：

>>> scipy.stats.gmean(y)
4.67788567485604
>>> scipy.stats.gmean(z)
4.67788567485604

您获得了与纯 Python 实现相同的结果。

如果nan数据集中有值，gmean()则将返回nan. 如果至少有一个0，那么它会返回0.0并发出警告。如果您提供至少一个负数，那么您将收到nan警告。

计算描述性统计量

首先导入您需要的所有包：

>>> import math
>>> import statistics
>>> import numpy as np
>>> import scipy.stats
>>> import pandas as pd

这些是 Python 统计计算所需的所有包。通常，您不会使用 Python 的内置math包，但它在本教程中会很有用。稍后，您将导入matplotlib.pyplot以进行数据可视化。

让我们创建一些数据来处理。您将从包含一些任意数字数据的 Python 列表开始：

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> x_with_nan = [8.0, 1, 2.5, math.nan, 4, 28.0]
>>> x
[8.0, 1, 2.5, 4, 28.0]
>>> x_with_nan
[8.0, 1, 2.5, nan, 4, 28.0]

现在您有了列表x和x_with_nan. 它们几乎相同，不同之处在于x_with_nan包含一个nan值。了解 Python 统计例程在遇到非数字值 ( nan)时的行为非常重要。在数据科学中，缺失值很常见，您经常将它们替换为nan.

>>> math.isnan(np.nan), np.isnan(math.nan)
(True, True)
>>> math.isnan(y_with_nan[3]), np.isnan(y_with_nan[3])
(True, True)

现在，创建对应于and 的np.ndarrayandpd.Series对象：xx_with_nan

>>> y, y_with_nan = np.array(x), np.array(x_with_nan)
>>> z, z_with_nan = pd.Series(x), pd.Series(x_with_nan)
>>> y
array([ 8. ,  1. ,  2.5, 4. , 28. ])
>>> y_with_nan
array([ 8. ,  1. ,  2.5,  nan,  4. , 28. ])
>>> z
0     8.0
1     1.0
2     2.5
3     4.0
4    28.0
dtype: float64
>>> z_with_nan
0     8.0
1     1.0
2     2.5
3     NaN
4     4.0
5    28.0
dtype: float64

您现在有两个 NumPy 数组（y和y_with_nan）和两个 Pandas Series（z和z_with_nan）。所有这些都是一维值序列。

您可以选择指定的每个值的标签z和z_with_nan。

中央倾向的措施

集中趋势的度量显示数据集的中心值或中间值。对于数据集的中心，有多种定义。在本教程中，您将学习如何识别和计算这些集中趋势的度量：

• 意思
• 加权平均数
• 几何平均数
• 谐波平均值
• 中位数
• 模式

绿点代表数据点 1、2.5、4、8 和 28。红色虚线是它们的平均值，或 (1 + 2.5 + 4 + 8 + 28) / 5 = 8.7。

您可以使用sum()和使用纯 Python 计算平均值len()，而无需导入库：

>>> mean_ = sum(x) / len(x)
>>> mean_
8.7

虽然这很干净优雅，但您也可以应用内置的 Python 统计函数：

>>> mean_ = statistics.mean(x)
>>> mean_
8.7
>>> mean_ = statistics.fmean(x)
>>> mean_
8.7

您已经从内置 Python库中调用了函数mean()和函数，并获得了与使用纯 Python 相同的结果。在Python 3.8 中引入作为. 它总是返回一个浮点数。fmean()statisticsfmean()mean()

但是，如果nan您的数据中有值，则statistics.mean()和statistics.fmean()将nan作为输出返回：

>>> mean_ = statistics.mean(x_with_nan)
>>> mean_
nan
>>> mean_ = statistics.fmean(x_with_nan)
>>> mean_
nan

此结果与 的行为一致sum()，因为sum(x_with_nan)也返回nan。

如果您使用 NumPy，那么您可以通过以下方式获得平均值np.mean()：

>>> mean_ = np.mean(y)
>>> mean_
8.7

在上面的例子中，mean()是一个函数，但你也可以使用相应的方法.mean()：

>>> mean_ = y.mean()
>>> mean_
8.7

NumPy的函数mean()和方法.mean()返回与statistics.mean(). 当nan您的数据中有值时，情况也是如此：

>>> np.mean(y_with_nan)
nan
>>> y_with_nan.mean()
nan

您通常不需要因此获得nan值。如果您更喜欢忽略nan值，则可以使用np.nanmean()：

>>> np.nanmean(y_with_nan)
8.7

nanmean()只是忽略所有nan值。它返回的值与mean()您将其应用于没有nan值的数据集相同。

pd.Series对象也有方法.mean()：

>>> mean_ = z.mean()
>>> mean_
8.7

如您所见，它的使用方式与 NumPy 的情况类似。但是，.mean()Pandasnan默认忽略值：

>>> z_with_nan.mean()
8.7

这种行为是可选参数的默认值的结果skipna。您可以更改此参数以修改行为。

加权平均数

该加权平均，也称为加权算术平均法或加权平均，是算术平均值，使您可以定义每个数据点到结果的相对贡献的推广。

您为数据集 𝑥 的每个数据点 𝑥ᵢ定义一个权重 𝑤ᵢ，其中 𝑖 = 1、2、……、𝑛 和 𝑛 是 𝑥 中的项目数。然后，您将每个数据点与相应的权重相乘，对所有乘积求和，并将获得的总和除以权重的总和：Σᵢ(𝑤ᵢ𝑥ᵢ) / Σᵢ𝑤ᵢ。

当您需要包含以给定相对频率出现的项目的数据集的平均值时，加权平均值非常方便。例如，假设您有一个集合，其中所有项目的 20% 等于 2，50% 的项目等于 4，其余 30% 的项目等于 8。您可以计算平均值这样的一套：

>>> 0.2 * 2 + 0.5 * 4 + 0.3 * 8
4.8

在这里，您将频率与权重一起考虑在内。使用此方法，您无需知道项目总数。

您可以通过sum()与range()或结合使用纯 Python 实现加权平均值zip()：

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> w = [0.1, 0.2, 0.3, 0.25, 0.15]
>>> wmean = sum(w[i] * x[i] for i in range(len(x))) / sum(w)
>>> wmean
6.95
>>> wmean = sum(x_ * w_ for (x_, w_) in zip(x, w)) / sum(w)
>>> wmean
6.95

同样，这是一个干净优雅的实现，您不需要导入任何库。

但是，如果您有大型数据集，那么 NumPy 可能会提供更好的解决方案。您可以使用np.average()来获取 NumPy 数组或 Pandas 的加权平均值Series：

>>> y, z, w = np.array(x), pd.Series(x), np.array(w)
>>> wmean = np.average(y, weights=w)
>>> wmean
6.95
>>> wmean = np.average(z, weights=w)
>>> wmean
6.95

结果与纯 Python 实现的情况相同。您也可以在普通列表和元组上使用此方法。

另一种解决方案是使用元素之积w * y与np.sum()或.sum()：

>>> (w * y).sum() / w.sum()
6.95

就是这样！您已经计算了加权平均值。

但是，如果您的数据集包含nan值，请小心：

>>> w = np.array([0.1, 0.2, 0.3, 0.0, 0.2, 0.1])
>>> (w * y_with_nan).sum() / w.sum()
nan
>>> np.average(y_with_nan, weights=w)
nan
>>> np.average(z_with_nan, weights=w)
nan

在这种情况下，average()返回nan，这与 一致np.mean()。

谐波平均值

的调和平均是倒数平均数据集中的所有项目的倒数的：𝑛/Σᵢ（1 /𝑥ᵢ），其中𝑖= 1，2，...，𝑛和𝑛是在数据集中𝑥项目的数量。调和平均值的纯 Python 实现的一种变体是：

>>> hmean = len(x) / sum(1 / item for item in x)
>>> hmean
2.7613412228796843

它与x您计算为 8.7的相同数据的算术平均值完全不同。

您还可以使用以下方法计算此度量statistics.harmonic_mean()：

>>> hmean = statistics.harmonic_mean(x)
>>> hmean
2.7613412228796843

上面的示例显示了statistics.harmonic_mean(). 如果您nan在数据集中有一个值，那么它会返回nan. 如果至少有一个0，那么它会返回0。如果您提供至少一个负数，那么您将得到statistics.StatisticsError：

>>> statistics.harmonic_mean(x_with_nan)
nan
>>> statistics.harmonic_mean([1, 0, 2])
0
>>> statistics.harmonic_mean([1, 2, -2])  # Raises StatisticsError

使用此方法时，请记住这三个场景！

计算调和平均值的第三种方法是使用scipy.stats.hmean()：

>>> scipy.stats.hmean(y)
2.7613412228796843
>>> scipy.stats.hmean(z)
2.7613412228796843

同样，这是一个非常简单的实现。但是，如果您的数据集包含nan、0、负数或除正数之外的任何内容，那么您将得到一个ValueError!

几何平均数

的几何平均值是所有𝑛元素的乘积的𝑛次方根𝑥ᵢ在数据集中𝑥：ⁿ√（Πᵢ𝑥ᵢ），其中𝑖= 1,2，...，𝑛。下图说明了数据集的算术、调和和几何平均值：

同样，绿点代表数据点 1、2.5、4、8 和 28。红色虚线是平均值。蓝色虚线是调和平均值，黄色虚线是几何平均值。

您可以像这样在纯 Python 中实现几何平均值：

>>> gmean = 1
>>> for item in x:
...     gmean *= item
...
>>> gmean **= 1 / len(x)
>>> gmean
4.677885674856041

如您所见，在这种情况下，几何平均值的值与同一数据集的算术平均值 (8.7) 和调和平均值 (2.76) 的值有显着差异x。

Python 3.8 引入了statistics.geometric_mean()，它将所有值转换为浮点数并返回它们的几何平均值：

>>> gmean = statistics.geometric_mean(x)
>>> gmean
4.67788567485604

您得到了与上一个示例相同的结果，但舍入误差最小。

如果您传递带有nan值的数据，statistics.geometric_mean()则将像大多数类似的函数一样运行并返回nan：

>>> gmean = statistics.geometric_mean(x_with_nan)
>>> gmean
nan

事实上，这与行为一致statistics.mean()，statistics.fmean()和statistics.harmonic_mean()。如果您的数据中有零或负数，statistics.geometric_mean()则将提高statistics.StatisticsError.

您还可以使用以下方法获得几何平均值scipy.stats.gmean()：

>>> scipy.stats.gmean(y)
4.67788567485604
>>> scipy.stats.gmean(z)
4.67788567485604

您获得了与纯 Python 实现相同的结果。

如果nan数据集中有值，gmean()则将返回nan. 如果至少有一个0，那么它会返回0.0并发出警告。如果您提供至少一个负数，那么您将收到nan警告。

中位数

的采样位数是一个有序数据集的中间元件。数据集可以按升序或降序排序。如果数据集的元素数𝑛为奇数，则中位数为中间位置的值：0.5(𝑛 + 1)。如果𝑛是偶数，那么中位数就是中间两个值的算术平均值，即0.5𝑛和0.5𝑛+1位置的项目。

例如，如果您有数据点 2、4、1、8 和 9，则中值为 4，它位于已排序数据集 (1, 2, 4, 8, 9) 的中间。如果数据点为 2、4、1 和 8，则中位数为 3，即已排序序列的两个中间元素（2 和 4）的平均值。下图说明了这一点：

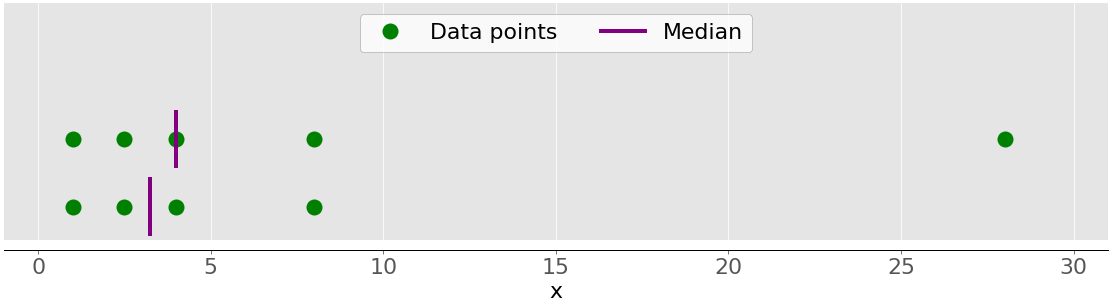
数据点是绿点，紫色线显示每个数据集的中位数。上层数据集（1、2.5、4、8 和 28）的中值是 4。如果从下层数据集中删除异常值 28，则中值变为 2.5 和 4 之间的算术平均值，即 3.25。

下图显示了数据点 1、2.5、4、8 和 28 的平均值和中位数：

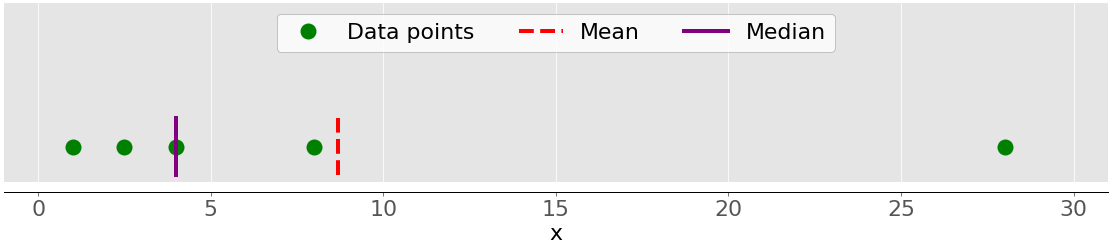
同样，平均值是红色虚线，而中位数是紫色线。

均值和中值行为之间的主要区别与数据集异常值或极值有关。均值受异常值的影响很大，但中位数仅轻微或完全不依赖于异常值。考虑下图：

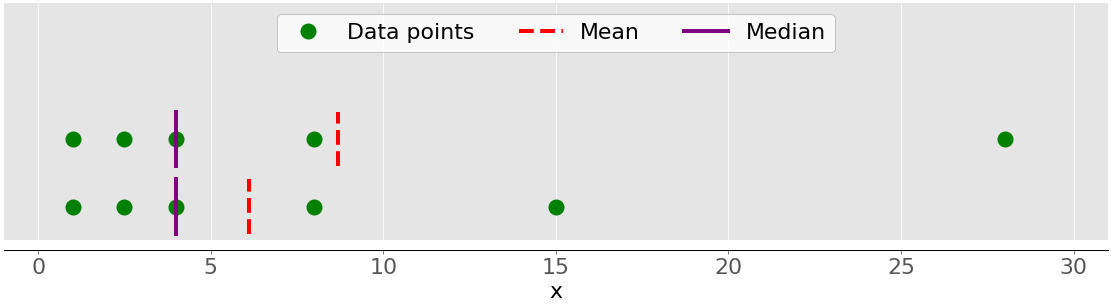
上面的数据集再次包含项目 1、2.5、4、8 和 28。正如您之前看到的，它的平均值是 8.7，中位数是 5。下面的数据集显示了当您移动值为 28 的最右侧点时发生的情况：

• 如果您增加其值（将其向右移动），则平均值将上升，但中值永远不会改变。
• 如果减小它的值（向左移动），则平均值将下降，但中位数将保持不变，直到移动点的值大于或等于 4。

您可以比较平均值和中位数，作为检测数据中异常值和不对称性的一种方法。平均值还是中值对您更有用取决于您的特定问题的上下文。

这是中位数的许多可能的纯 Python 实现之一：

>>> n = len(x)
>>> if n % 2:
...     median_ = sorted(x)[round(0.5*(n-1))]
... else:
...     x_ord, index = sorted(x), round(0.5 * n)
...     median_ = 0.5 * (x_ord[index-1] + x_ord[index])
...
>>> median_
4

此实现的两个最重要的步骤如下：

1. 对数据集的元素进行排序
2. 在已排序的数据集中查找中间元素

您可以通过以下方式获得中位数statistics.median()：

>>> median_ = statistics.median(x)
>>> median_
4
>>> median_ = statistics.median(x[:-1])
>>> median_
3.25

的排序版本x的[1, 2.5, 4, 8.0, 28.0]，所以中间的元素4。排序版本的x[:-1]，这是x没有的最后一个项目28.0，是[1, 2.5, 4, 8.0]。现在，有两个中间元素，2.5和4。他们的平均值是3.25。

median_low()而且median_high()是两个更关系到在Python中值函数statistics库。他们总是从数据集中返回一个元素：

• 如果元素的数量是奇数，那么只有一个中间值，所以这些函数的行为就像median()。
• 如果元素数为 even，则有两个中间值。在这种情况下，median_low()返回较低和median_high()较高的中间值。

您可以像使用一样使用这些函数median()：

>>> statistics.median_low(x[:-1])
2.5
>>> statistics.median_high(x[:-1])
4

同样， 的排序版本x[:-1]是[1, 2.5, 4, 8.0]。中间的两个元素是2.5（低）和4（高）。

与 Pythonstatistics库中的大多数其他函数不同，当数据点中有值时median()，median_low()、 和median_high()不返回：nannan

>>> statistics.median(x_with_nan)
6.0
>>> statistics.median_low(x_with_nan)
4
>>> statistics.median_high(x_with_nan)
8.0

当心这种行为，因为它可能不是你想要的！

您还可以通过以下方式获得中位数np.median()：

>>> median_ = np.median(y)
>>> median_
4.0
>>> median_ = np.median(y[:-1])
>>> median_
3.25

您已获得与statistics.median()和相同的值np.median()。

但是，如果nan您的数据集中有值，则np.median()发出RuntimeWarning并返回nan。如果此行为不是您想要的，那么您可以使用nanmedian()忽略所有nan值：

>>> np.nanmedian(y_with_nan)
4.0
>>> np.nanmedian(y_with_nan[:-1])
3.25

获得的结果与statistics.median()和np.median()应用于数据集x和y。

PandasSeries对象具有默认.median()忽略nan值的方法：

>>> z.median()
4.0
>>> z_with_nan.median()
4.0

的行为.median()与.mean()Pandas 中的一致。您可以使用可选参数更改此行为skipna。

模式

该采样模式是在最频繁出现的数据集中的值。如果没有单个这样的值，则该集合是多模态的，因为它具有多个模态值。例如，在包含点 2、3、2、8 和 12 的集合中，数字 2 是众数，因为它出现了两次，而其他项只出现一次。

这是使用纯 Python 获取模式的方法：

>>> u = [2, 3, 2, 8, 12]
>>> mode_ = max((u.count(item), item) for item in set(u))[1]
>>> mode_
2

您使用u.count()来获取 中每个项目的出现次数u。出现次数最多的项目是众数。请注意，您不必使用set(u). 相反，您可以将其替换为 justu并遍历整个列表。

您可以使用statistics.mode()和获取模式statistics.multimode()：

>>> mode_ = statistics.mode(u)
>>> mode_
>>> mode_ = statistics.multimode(u)
>>> mode_
[2]

如您所见，mode()返回单个值，同时multimode()返回包含结果的列表。但这并不是这两个函数之间的唯一区别。如果有多个模式值，则mode()raises StatisticsError，同时multimode()返回包含所有模式的列表：

>>> v = [12, 15, 12, 15, 21, 15, 12]
>>> statistics.mode(v)  # Raises StatisticsError
>>> statistics.multimode(v)
[12, 15]

您应该特别注意这种情况，并在这两个函数之间进行选择时要小心。

statistics.mode()并将值作为常规值statistics.multimode()处理nan并且可以nan作为模态值返回：

>>> statistics.mode([2, math.nan, 2])
2
>>> statistics.multimode([2, math.nan, 2])
[2]
>>> statistics.mode([2, math.nan, 0, math.nan, 5])
nan
>>> statistics.multimode([2, math.nan, 0, math.nan, 5])
[nan]

在上面的第一个示例中，数字2出现两次并且是模态值。在第二个示例中，nan是模态值，因为它出现两次，而其他值只出现一次。

您还可以通过以下方式获取模式scipy.stats.mode()：

>>> u, v = np.array(u), np.array(v)
>>> mode_ = scipy.stats.mode(u)
>>> mode_
ModeResult(mode=array([2]), count=array([2]))
>>> mode_ = scipy.stats.mode(v)
>>> mode_
ModeResult(mode=array([12]), count=array([3]))

此函数返回具有模态值及其出现次数的对象。如果数据集中有多个模态值，则只返回最小值。

您可以使用点符号将模式及其出现次数作为 NumPy 数组获取：

>>> mode_.mode
array([12])
>>> mode_.count
array([3])

此代码用于.mode返回12数组中的最小模式 ( )v并.count返回它出现的次数 ( 3)。价值观scipy.stats.mode()也很灵活nan。它允许您使用可选参数定义所需的行为nan_policy。此参数可以采用值'propagate'、'raise'（错误）或'omit'。

PandasSeries对象的方法.mode()可以很好地处理多模式值并nan默认忽略值：

>>> u, v, w = pd.Series(u), pd.Series(v), pd.Series([2, 2, math.nan])
>>> u.mode()
0    2
dtype: int64
>>> v.mode()
0    12
1    15
dtype: int64
>>> w.mode()
0    2.0
dtype: float64

如您所见，.mode()返回一个pd.Series包含所有模态值的 new 。如果要.mode()考虑nan值，则只需传递可选参数dropna=False。

变异性度量

集中趋势的度量不足以描述数据。您还需要量化数据点分布的可变性度量。在本节中，您将学习如何识别和计算以下可变性度量：

• 方差
• 标准差
• 偏度
• 百分位数
• 范围

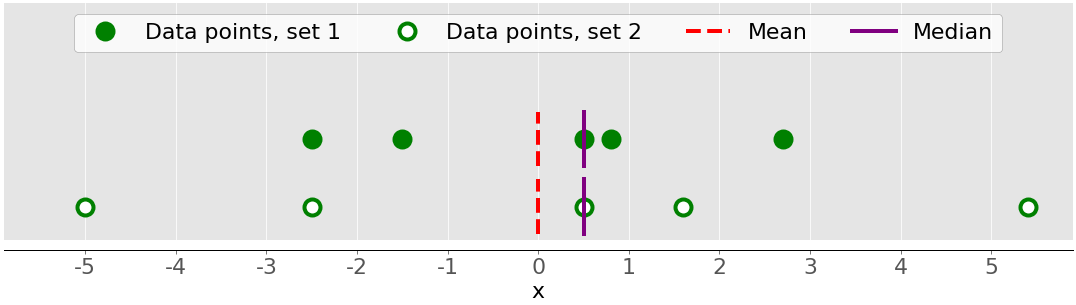
图中有两个数据集：

1. 绿点：此数据集的方差较小或与平均值的平均差异较小。它还具有较小的范围或最大和最小项目之间的较小差异。
2. 白点：此数据集具有较大的方差或与均值的平均差异较大。它也有更大的范围或最大和最小项目之间的更大差异。

请注意，这两个数据集具有相同的均值和中位数，即使它们看起来有显着差异。平均值和中位数都无法描述这种差异。这就是为什么您需要可变性度量的原因。

以下是使用纯 Python 计算样本方差的方法：

>>> n = len(x)
>>> mean_ = sum(x) / n
>>> var_ = sum((item - mean_)**2 for item in x) / (n - 1)
>>> var_
123.19999999999999

这种方法就足够了，并且可以很好地计算样本方差。然而，更短、更优雅的解决方案是调用现有函数statistics.variance()：

>>> var_ = statistics.variance(x)
>>> var_
123.2

您已获得与上述方差相同的结果。variance()可避免计算平均值，如果你提供明确平均值作为第二个参数：statistics.variance(x, mean_)。

如果您nan的数据中有值，statistics.variance()则将返回nan：

>>> statistics.variance(x_with_nan)
nan

此行为与mean()Pythonstatistics库中的大多数其他函数一致。

您还可以使用 NumPy 计算样本方差。您应该使用该函数np.var()或相应的方法.var()：

>>> var_ = np.var(y, ddof=1)
>>> var_
123.19999999999999
>>> var_ = y.var(ddof=1)
>>> var_
123.19999999999999

指定参数非常重要ddof=1。这就是您如何将delta 自由度设置为1。此参数允许正确计算 𝑠²，在分母中使用 (𝑛 − 1) 而不是 𝑛。

如果nan数据集中有值，则np.var()和.var()将返回nan：

>>> np.var(y_with_nan, ddof=1)
nan
>>> y_with_nan.var(ddof=1)
nan

这与np.mean()和一致np.average()。如果你想跳过nan值，那么你应该使用np.nanvar()：

>>> np.nanvar(y_with_nan, ddof=1)
123.19999999999999

np.nanvar()忽略nan值。它还需要您指定ddof=1.

pd.Series对象具有默认.var()跳过nan值的方法：

>>> z.var(ddof=1)
123.19999999999999
>>> z_with_nan.var(ddof=1)
123.19999999999999

它也有参数ddof，但它的默认值是1，所以你可以省略它。如果您想要与nan值相关的不同行为，请使用可选参数skipna。

你计算总体方差类似于样本方差。但是，您必须在分母中使用 𝑛 而不是 𝑛 − 1：Σᵢ(𝑥ᵢ − mean(𝑥))² / 𝑛。在这种情况下，𝑛 是整个总体中的项目数。可以得到与样本方差相似的总体方差，区别如下：

• 在纯 Python 实现中替换(n - 1)为n。
• 使用 statistics.pvariance()代替statistics.variance()。
• ddof=0如果您使用 NumPy 或 Pandas，请指定参数。在 NumPy 中，您可以省略，ddof因为它的默认值为0。

请注意，无论何时计算方差，您都应该始终注意您是在处理样本还是整个总体！

>>> std_ = var_ ** 0.5
>>> std_
11.099549540409285

>>> std_ = statistics.stdev(x)
>>> std_
11.099549540409287

>>> np.std(y, ddof=1)
11.099549540409285
>>> y.std(ddof=1)
11.099549540409285
>>> np.std(y_with_nan, ddof=1)
nan
>>> y_with_nan.std(ddof=1)
nan
>>> np.nanstd(y_with_nan, ddof=1)
11.099549540409285

>>> z.std(ddof=1)
11.099549540409285
>>> z_with_nan.std(ddof=1)
11.099549540409285

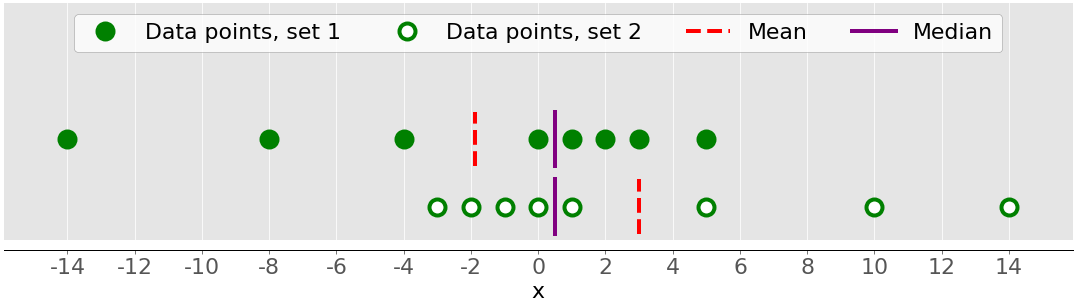
第一组由绿色圆点表示，第二组由白色圆点表示。通常，负偏度值表示左侧有显性尾部，您可以在第一组中看到。正偏度值对应于右侧更长或更胖的尾巴，您可以在第二组中看到。如果偏度接近 0（例如，介于 -0.5 和 0.5 之间），则认为数据集非常对称。

一旦计算了数据集的大小n、样本均值mean_和标准偏差std_，就可以使用纯 Python 获得样本偏度：

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> n = len(x)
>>> mean_ = sum(x) / n
>>> var_ = sum((item - mean_)**2 for item in x) / (n - 1)
>>> std_ = var_ ** 0.5
>>> skew_ = (sum((item - mean_)**3 for item in x)
...          * n / ((n - 1) * (n - 2) * std_**3))
>>> skew_
1.9470432273905929

偏度是正的，所以x有一个右侧的尾巴。

您还可以使用以下方法计算样本偏度scipy.stats.skew()：

>>> y, y_with_nan = np.array(x), np.array(x_with_nan)
>>> scipy.stats.skew(y, bias=False)
1.9470432273905927
>>> scipy.stats.skew(y_with_nan, bias=False)
nan

得到的结果和纯Python实现一样。该参数bias设置为False启用对统计偏差的校正。可选参数nan_policy的值可以取'propagate'，'raise'或'omit'。它允许您控制处理nan值的方式。

PandasSeries对象具有.skew()返回数据集偏度的方法：

>>> z, z_with_nan = pd.Series(x), pd.Series(x_with_nan)
>>> z.skew()
1.9470432273905924
>>> z_with_nan.skew()
1.9470432273905924

与其他方法一样，默认情况下.skew()忽略nan值，因为可选参数的默认值skipna。

百分位数

所述样品𝑝百分使得在数据集中的元素𝑝％小于或等于该值在数据集中的元素。此外，(100 − 𝑝)% 的元素大于或等于该值。如果数据集中有两个这样的元素，那么样本𝑝百分位数就是它们的算术平均值。每个数据集都有三个四分位数，它们是将数据集分为四个部分的百分位数：

• 第一个四分位数是样本的第 25 个百分位数。它从数据集的其余部分中划分出大约 25% 的最小项目。
• 第二个四分位数是样本的第 50 个百分位数或中位数。大约 25% 的项目位于第一和第二四分位数之间，另外 25% 位于第二和第三四分位数之间。
• 第三个四分位数是样本的第 75 个百分位数。它从数据集的其余部分中划分出大约 25% 的最大项目。

每个部分具有大致相同数量的项目。如果要将数据划分为多个间隔，则可以使用statistics.quantiles()：

>>> x = [-5.0, -1.1, 0.1, 2.0, 8.0, 12.8, 21.0, 25.8, 41.0]
>>> statistics.quantiles(x, n=2)
[8.0]
>>> statistics.quantiles(x, n=4, method='inclusive')
[0.1, 8.0, 21.0]

在本例中，8.0是 的中位数x，而0.1和21.0分别是样本第 25 和第 75 个百分位数。该参数n定义生成的等概率百分位数的数量，并method确定如何计算它们。

您还可以np.percentile()用于确定数据集中的任何样本百分位数。例如，您可以通过以下方式找到第 5 个和第 95 个百分位数：

>>> y = np.array(x)
>>> np.percentile(y, 5)
-3.44
>>> np.percentile(y, 95)
34.919999999999995

percentile()需要几个参数。您必须提供数据集作为第一个参数，百分位值作为第二个参数。数据集可以是 NumPy 数组、列表、元组或类似数据结构的形式。百分位数可以是 0 到 100 之间的数字，如上例所示，但也可以是数字序列：

>>> np.percentile(y, [25, 50, 75])
array([ 0.1,  8. , 21. ])
>>> np.median(y)
8.0

此代码一次计算第 25 个、第 50 个和第 75 个百分位数。如果百分位值是一个序列，则percentile()返回一个带有结果的 NumPy 数组。第一条语句返回四分位数数组。第二个语句返回中位数，因此您可以确认它等于第 50 个百分位数，即8.0。

如果要忽略nan值，请np.nanpercentile()改用：

>>> y_with_nan = np.insert(y, 2, np.nan)
>>> y_with_nan
array([-5. , -1.1,  nan,  0.1,  2. ,  8. , 12.8, 21. , 25.8, 41. ])
>>> np.nanpercentile(y_with_nan, [25, 50, 75])
array([ 0.1,  8. , 21. ])

这就是您可以避免nan值的方法。

NumPy的还为您提供非常相似的功能中quantile()和nanquantile()。如果使用它们，则需要提供分位数值作为 0 到 1 之间的数字而不是百分位数：

>>> np.quantile(y, 0.05)
-3.44
>>> np.quantile(y, 0.95)
34.919999999999995
>>> np.quantile(y, [0.25, 0.5, 0.75])
array([ 0.1,  8. , 21. ])
>>> np.nanquantile(y_with_nan, [0.25, 0.5, 0.75])
array([ 0.1,  8. , 21. ])

结果与前面的示例相同，但这里的参数介于 0 和 1 之间。换句话说，您传递了0.05而不是5和0.95而不是95。

pd.Series对象有方法.quantile()：

>>> z, z_with_nan = pd.Series(y), pd.Series(y_with_nan)
>>> z.quantile(0.05)
-3.44
>>> z.quantile(0.95)
34.919999999999995
>>> z.quantile([0.25, 0.5, 0.75])
0.25     0.1
0.50     8.0
0.75    21.0
dtype: float64
>>> z_with_nan.quantile([0.25, 0.5, 0.75])
0.25     0.1
0.50     8.0
0.75    21.0
dtype: float64

.quantile()还需要您提供分位数值作为参数。该值可以是 0 到 1 之间的数字或数字序列。在第一种情况下，.quantile()返回一个标量。在第二种情况下，它返回一个新的Series保存结果。

范围

的数据的范围是在数据集中的最大和最小元件之间的差异。您可以使用以下功能获取它np.ptp()：

>>> np.ptp(y)
46.0
>>> np.ptp(z)
46.0
>>> np.ptp(y_with_nan)
nan
>>> np.ptp(z_with_nan)
46.0

nan如果nanNumPy 数组中有值，则此函数返回。如果您使用 PandasSeries对象，那么它将返回一个数字。

或者，您可以使用内置的 Python、NumPy 或 Pandas 函数和方法来计算序列的最大值和最小值：

• max()和min()来自 Python 标准库
• amax()并amin()从NumPy的
• nanmax()并nanmin()从 NumPy 忽略nan值
• .max()并.min()从NumPy的
• .max()并.min()从 Pandasnan默认忽略值

以下是有关如何使用这些例程的一些示例：

>>> np.amax(y) - np.amin(y)
46.0
>>> np.nanmax(y_with_nan) - np.nanmin(y_with_nan)
46.0
>>> y.max() - y.min()
46.0
>>> z.max() - z.min()
46.0
>>> z_with_nan.max() - z_with_nan.min()
46.0

这就是您获得数据范围的方式。

该四分位范围是在第一和第三个四分位数之间的差值。计算四分位数后，您可以计算它们的差值：

>>> quartiles = np.quantile(y, [0.25, 0.75])
>>> quartiles[1] - quartiles[0]
20.9
>>> quartiles = z.quantile([0.25, 0.75])
>>> quartiles[0.75] - quartiles[0.25]
20.9

请注意，您可以Series使用标签0.75和访问 Pandas对象中的值0.25。

描述性统计总结

SciPy 和 Pandas 提供了有用的例程，可以通过单个函数或方法调用快速获取描述性统计信息。您可以像这样使用scipy.stats.describe()：

>>> result = scipy.stats.describe(y, ddof=1, bias=False)
>>> result
DescribeResult(nobs=9, minmax=(-5.0, 41.0), mean=11.622222222222222, variance=228.75194444444446, skewness=0.9249043136685094, kurtosis=0.14770623629658886)

您必须提供数据集作为第一个参数。参数可以是 NumPy 数组、列表、元组或类似的数据结构。您可以省略，ddof=1因为它是默认值，并且仅在计算方差时才重要。您可以通过bias=False强制纠正统计偏差的偏度和峰度。

describe() 返回一个包含以下描述性统计信息的对象：

• nobs：数据集中观察或元素的数量
• minmax：具有数据集最小值和最大值的元组
• mean：数据集的平均值
• variance：数据集的方差
• skewness：数据集的偏度
• kurtosis：数据集的峰度

您可以使用点表示法访问特定值：

>>> result.nobs
9
>>> result.minmax[0]  # Min
-5.0
>>> result.minmax[1]  # Max
41.0
>>> result.mean
11.622222222222222
>>> result.variance
228.75194444444446
>>> result.skewness
0.9249043136685094
>>> result.kurtosis
0.14770623629658886

使用 SciPy，您只需一个函数调用即可获得数据集的描述性统计摘要。

Pandas 具有类似的，甚至更好的功能。Series对象有方法.describe()：

>>> result = z.describe()
>>> result
count     9.000000
mean     11.622222
std      15.124548
min      -5.000000
25%       0.100000
50%       8.000000
75%      21.000000
max      41.000000
dtype: float64

它返回一个新的Series，其中包含以下内容：

• count：数据集中元素的数量
• mean：数据集的平均值
• std：数据集的标准偏差
• minand max：数据集的最小值和最大值
• 25%, 50%, 和75%：数据集的四分位数

如果您希望结果Series对象包含其他百分位数，则应指定可选参数的值percentiles。您可以使用result其标签访问每个项目：

>>> result['mean']
11.622222222222222
>>> result['std']
15.12454774346805
>>> result['min']
-5.0
>>> result['max']
41.0
>>> result['25%']
0.1
>>> result['50%']
8.0
>>> result['75%']
21.0

这就是如何Series使用 Pandas 通过单个方法调用获取对象的描述性统计信息。

数据对之间相关性的度量

您经常需要检查数据集中两个变量的对应元素之间的关系。假设有两个变量，𝑥 和 𝑦，具有相同数量的元素，𝑛。让𝑥₁从𝑥对应𝑦₁从𝑦，𝑥₂从𝑥到𝑦₂从𝑦，依此类推。然后你可以说有𝑛对对应的元素：(𝑥₁, 𝑦₁), (𝑥₂, 𝑦₂), 等等。

您将看到以下数据对之间相关性的度量：

• 当 𝑥 的较大值对应于 𝑦 的较大值时，存在正相关，反之亦然。
• 当 𝑥 的较大值对应于 𝑦 的较小值时，存在负相关，反之亦然。
• 如果没有这种明显的关系，则存在弱相关或不存在相关。

下图显示了负相关、弱相关和正相关的示例：

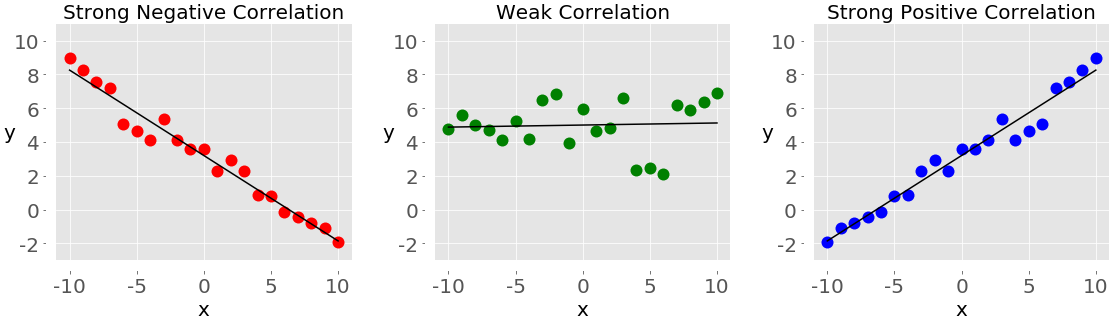
左侧带有红点的图显示负相关。中间带有绿点的图显示了弱相关性。最后，右侧带有蓝点的图显示正相关。

衡量数据集之间相关性的两个统计量是协方差和相关系数。让我们定义一些数据来处理这些度量。您将创建两个 Python 列表并使用它们来获取相应的 NumPy 数组和 Pandas Series：

>>> x = list(range(-10, 11))
>>> y = [0, 2, 2, 2, 2, 3, 3, 6, 7, 4, 7, 6, 6, 9, 4, 5, 5, 10, 11, 12, 14]
>>> x_, y_ = np.array(x), np.array(y)
>>> x__, y__ = pd.Series(x_), pd.Series(y_)

现在您有了这两个变量，您可以开始探索它们之间的关系。

>>> n = len(x)
>>> mean_x, mean_y = sum(x) / n, sum(y) / n
>>> cov_xy = (sum((x[k] - mean_x) * (y[k] - mean_y) for k in range(n))
...           / (n - 1))
>>> cov_xy
19.95

>>> cov_matrix = np.cov(x_, y_)
>>> cov_matrix
array([[38.5       , 19.95      ],
       [19.95      , 13.91428571]])

>>> x_.var(ddof=1)
38.5
>>> y_.var(ddof=1)
13.914285714285711

>>> cov_xy = cov_matrix[0, 1]
>>> cov_xy
19.95
>>> cov_xy = cov_matrix[1, 0]
>>> cov_xy
19.95

>>> cov_xy = x__.cov(y__)
>>> cov_xy
19.95
>>> cov_xy = y__.cov(x__)
>>> cov_xy
19.95

相关系数

的相关系数，或皮尔逊积矩相关系数，由符号𝑟表示。系数是数据之间相关性的另一种度量。您可以将其视为标准化协方差。以下是有关它的一些重要事实：

• 值 𝑟 > 0表示正相关。
• 值 𝑟 < 0表示负相关。
• 值 r = 1是 𝑟 的最大可能值。它对应于变量之间的完美正线性关系。
• 值 r = -1是 𝑟 的最小可能值。它对应于变量之间的完美负线性关系。
• 值 r ≈ 0，或者当 𝑟 大约为零时，意味着变量之间的相关性很弱。

相关系数的数学公式为𝑟 = 𝑠ˣʸ / (𝑠ˣ𝑠ʸ) 其中𝑠ˣ和𝑠ʸ分别是𝑥和𝑦的标准差。如果您有数据集and的均值 ( mean_xand mean_y) 和标准差 ( std_x, std_y)以及它们的 covariance ，那么您可以使用纯 Python 计算相关系数：xycov_xy

>>> var_x = sum((item - mean_x)**2 for item in x) / (n - 1)
>>> var_y = sum((item - mean_y)**2 for item in y) / (n - 1)
>>> std_x, std_y = var_x ** 0.5, var_y ** 0.5
>>> r = cov_xy / (std_x * std_y)
>>> r
0.861950005631606

您已经获得了r表示相关系数的变量。

scipy.stats具有pearsonr()计算相关系数和𝑝 值的例程：

>>> r, p = scipy.stats.pearsonr(x_, y_)
>>> r
0.861950005631606
>>> p
5.122760847201171e-07

pearsonr()返回一个包含两个数字的元组。第一个是 𝑟，第二个是 𝑝 值。

类似于协方差矩阵的情况下，可以申请np.corrcoef()使用x_，并y_作为参数，并得到相关系数矩阵：

>>> corr_matrix = np.corrcoef(x_, y_)
>>> corr_matrix
array([[1.        , 0.86195001],
       [0.86195001, 1.        ]])

左上角的元素是x_和之间的相关系数x_。右下方的元素是y_和之间的相关系数y_。它们的值等于1.0。其他两个元素相等，代表x_和之间的实际相关系数y_：

>>> r = corr_matrix[0, 1]
>>> r
0.8619500056316061
>>> r = corr_matrix[1, 0]
>>> r
0.861950005631606

当然，结果与纯 Python 和pearsonr().

您可以通过以下方式获得相关系数scipy.stats.linregress()：

>>> scipy.stats.linregress(x_, y_)
LinregressResult(slope=0.5181818181818181, intercept=5.714285714285714, rvalue=0.861950005631606, pvalue=5.122760847201164e-07, stderr=0.06992387660074979)

linregress()接受x_和y_，执行线性回归，并返回结果。slope并intercept定义回归线的方程，而rvalue是相关系数。要访问 的结果中的特定值linregress()，包括相关系数，请使用点表示法：

>>> result = scipy.stats.linregress(x_, y_)
>>> r = result.rvalue
>>> r
0.861950005631606

这就是您可以执行线性回归并获得相关系数的方法。

PandasSeries有.corr()计算相关系数的方法：

>>> r = x__.corr(y__)
>>> r
0.8619500056316061
>>> r = y__.corr(x__)
>>> r
0.861950005631606

您应该调用.corr()一个Series对象并将另一个对象作为第一个参数传递。