冒泡排序

冒泡排序（英语：Bubble Sort）是一种简单的排序算法。它重复地遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

排序过程

• 比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
• 针对所有的元素重复以上的步骤，除了最后一个。
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

交换过程图示(第一次)：

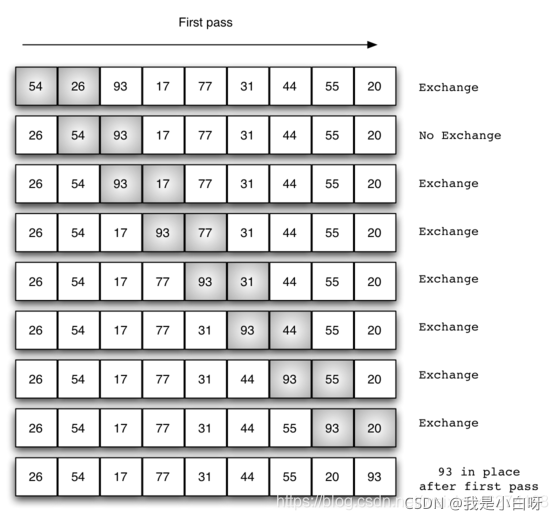
那么我们需要进行n-1次冒泡过程，每次对应的比较次数如下图所示：

​​​​

代码实现

时间复杂度

最优时间复杂度：O(n) （表示遍历一次发现没有任何可以交换的元素，排序结束。）
最坏时间复杂度：O(n^2)
稳定性：稳定

​

选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

排序过程

代码实现

时间复杂度

最优时间复杂度：O(n)
最坏时间复杂度：O(n^2)
稳定性：不稳定（考虑升序每次选择最大的情况）

快速排序

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

排序过程

• 从数列中挑出一个元素，称为"基准"（pivot）
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
  递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去

时间复杂度

最优时间复杂度：O(nlogn)
最坏时间复杂度：O(n2)
稳定性：不稳定
从一开始快速排序平均需要花费O(n log n)时间的描述并不明显。但是不难观察到的是分区运算，数组的元素都会在每次循环中走访过一次，使用O(n)的时间。在使用结合（concatenation）的版本中，这项运算也是O(n)。

在最好的情况，每次我们运行一次分区，我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。因此，在到达大小为一的数列前，我们只要作log n次嵌套的调用。这个意思就是调用树的深度是O(log n)。但是在同一层次结构的两个程序调用中，不会处理到原来数列的相同部分；因此，程序调用的每一层次结构总共全部仅需要O(n)的时间（每个调用有某些共同的额外耗费，但是因为在每一层次结构仅仅只有O(n)个调用，这些被归纳在O(n)系数中）。结果是这个算法仅需使用O(n log n)时间。

插入排序

插入排序（英语：Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

排序过程

代码实现

时间复杂度

最优时间复杂度：O(n) （升序排列，序列已经处于升序状态）
最坏时间复杂度：O(n2)
稳定性：稳定