决策树:如何创建完美的决策树?
一个决策树在现实生活中的许多类比和原来,它已经影响了广域中号AC海因学习,涵盖ç lassification 和回归。在决策分析中,决策树可用于直观地、明确地表示决策和决策制定。
因此,我将在本博客中介绍的内容大纲如下。
- 什么是决策树?
- 决策树的优缺点
- 创建决策树
什么是决策树?
决策树是一系列相关选择的可能结果的映射。它允许个人或组织根据成本、概率和收益权衡可能采取的行动。
顾名思义,它使用树状决策模型。它们可用于推动非正式讨论或制定算法,以数学方式预测最佳选择。
决策树通常以单个节点开始,该节点分支为可能的结果。这些结果中的每一个都会导致额外的节点,这些节点分支为其他可能性。这使它具有树状形状。
存在三种不同类型的节点:机会节点、决策节点和结束节点。由圆圈表示的机会节点显示某些结果的概率。由方块表示的决策节点显示要做出的决策,而末端节点显示决策路径的最终结果。
决策树的优缺点
优点
- 决策树生成可理解的规则。
- 决策树无需大量计算即可执行分类。
- 决策树能够处理连续变量和分类变量。
- 决策树清楚地表明哪些字段对预测或分类最重要。
缺点
- 决策树不太适合目标是预测连续属性值的估计任务。
- 决策树在分类问题中容易出错,类别多,训练样本相对较少。
- 训练决策树在计算上可能很昂贵。生长决策树的过程在计算上是昂贵的。在每个节点上,必须对每个候选分裂字段进行排序,然后才能找到其最佳分裂。在某些算法中,使用字段组合并且必须搜索最佳组合权重。修剪算法也可能很昂贵,因为必须形成和比较许多候选子树。
创建决策树
让我们考虑一组天文学家发现一颗新行星的场景。现在的问题是它是否会成为“下一个地球”?这个问题的答案将彻底改变人们的生活方式。嗯,字面意思!
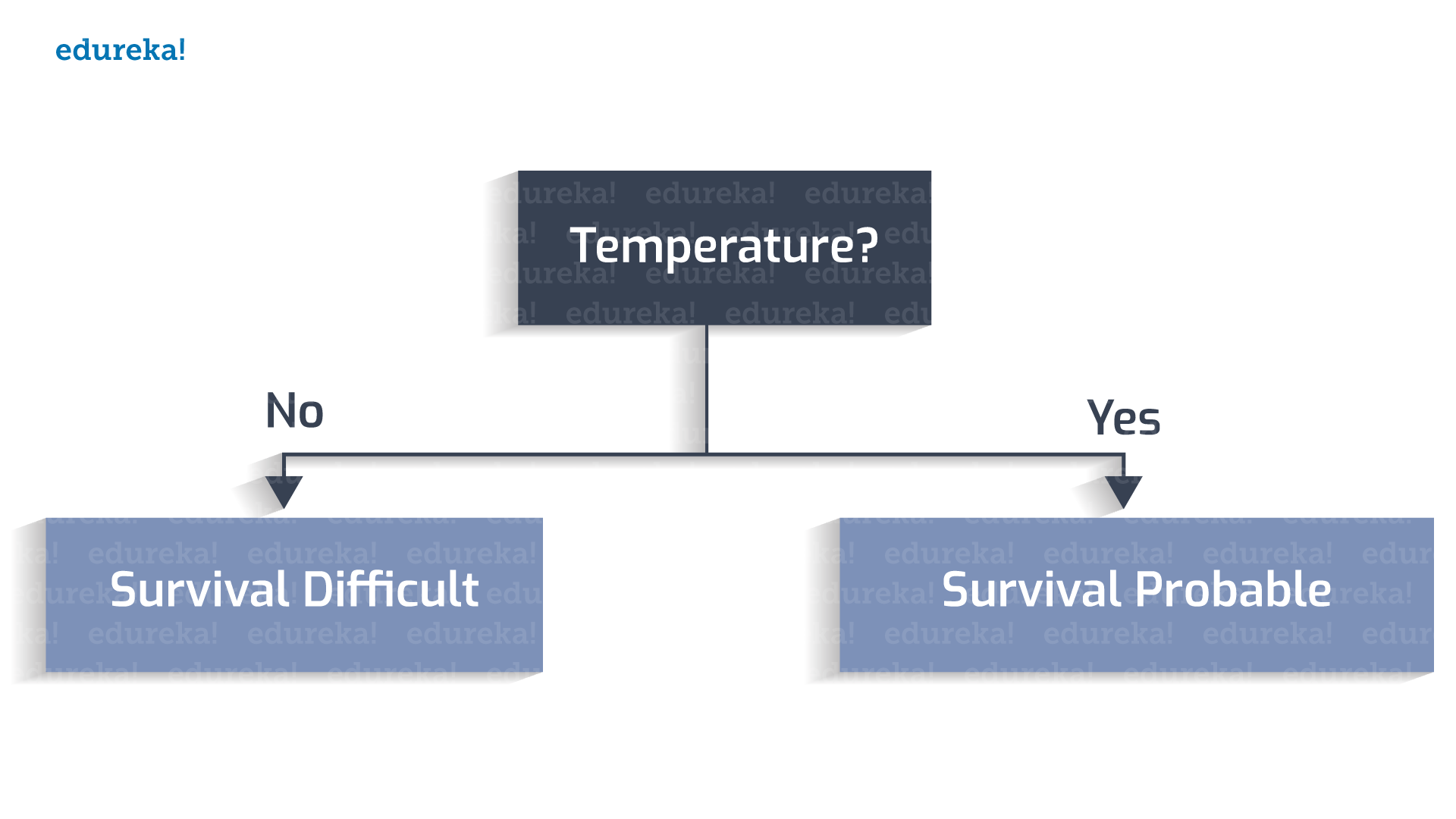
有 n 个决定因素需要彻底研究才能做出明智的决定。这些因素可能是地球上是否存在水、温度是多少、地表是否容易遭受持续风暴、动植物群是否能够在气候中存活等。
让我们创建一个决策树来确定我们是否发现了新的栖息地。
宜居温度在 0 到 100 摄氏度之间。
水是否存在?
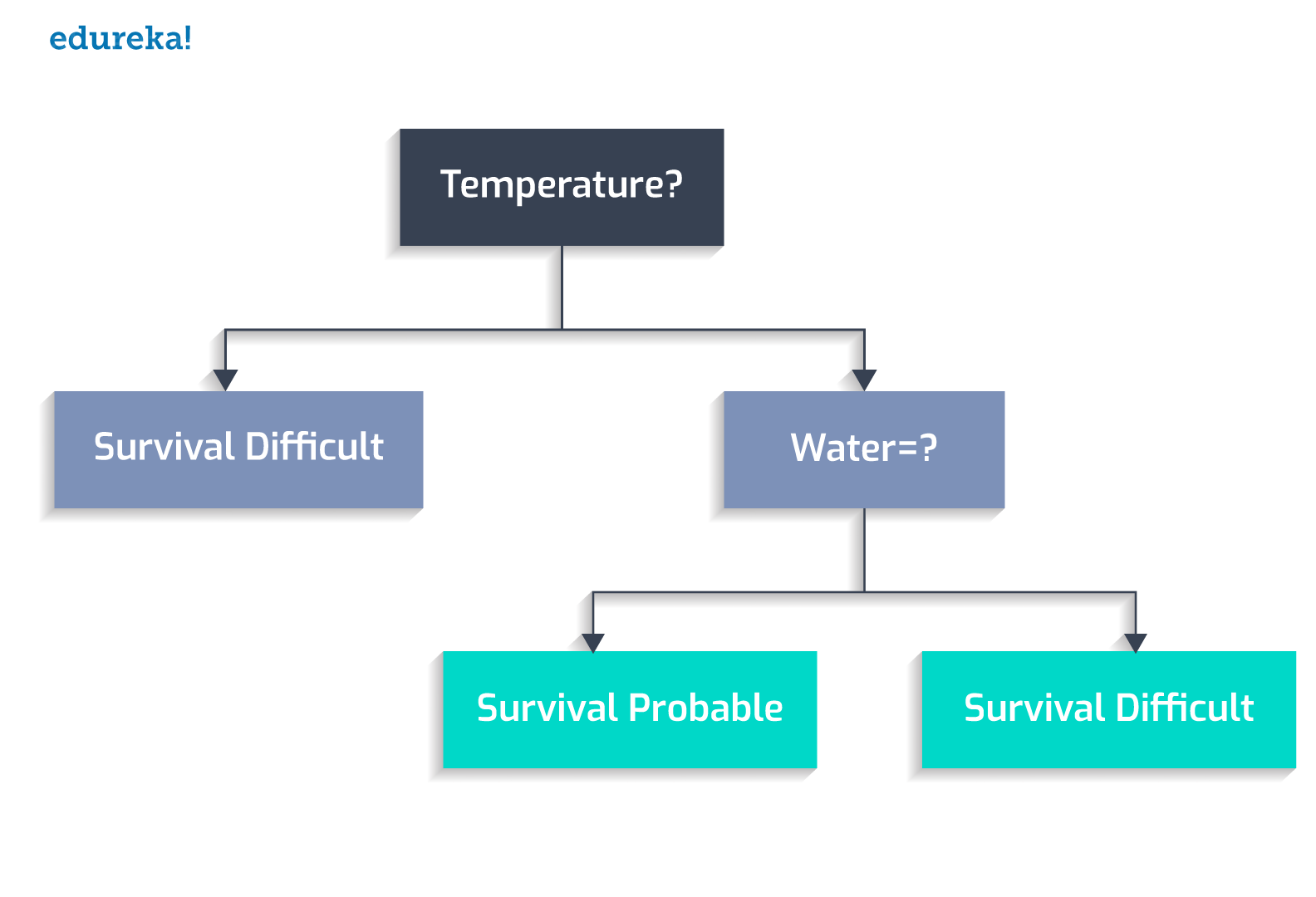
动植物是否繁盛?
地球表面有暴风雨?
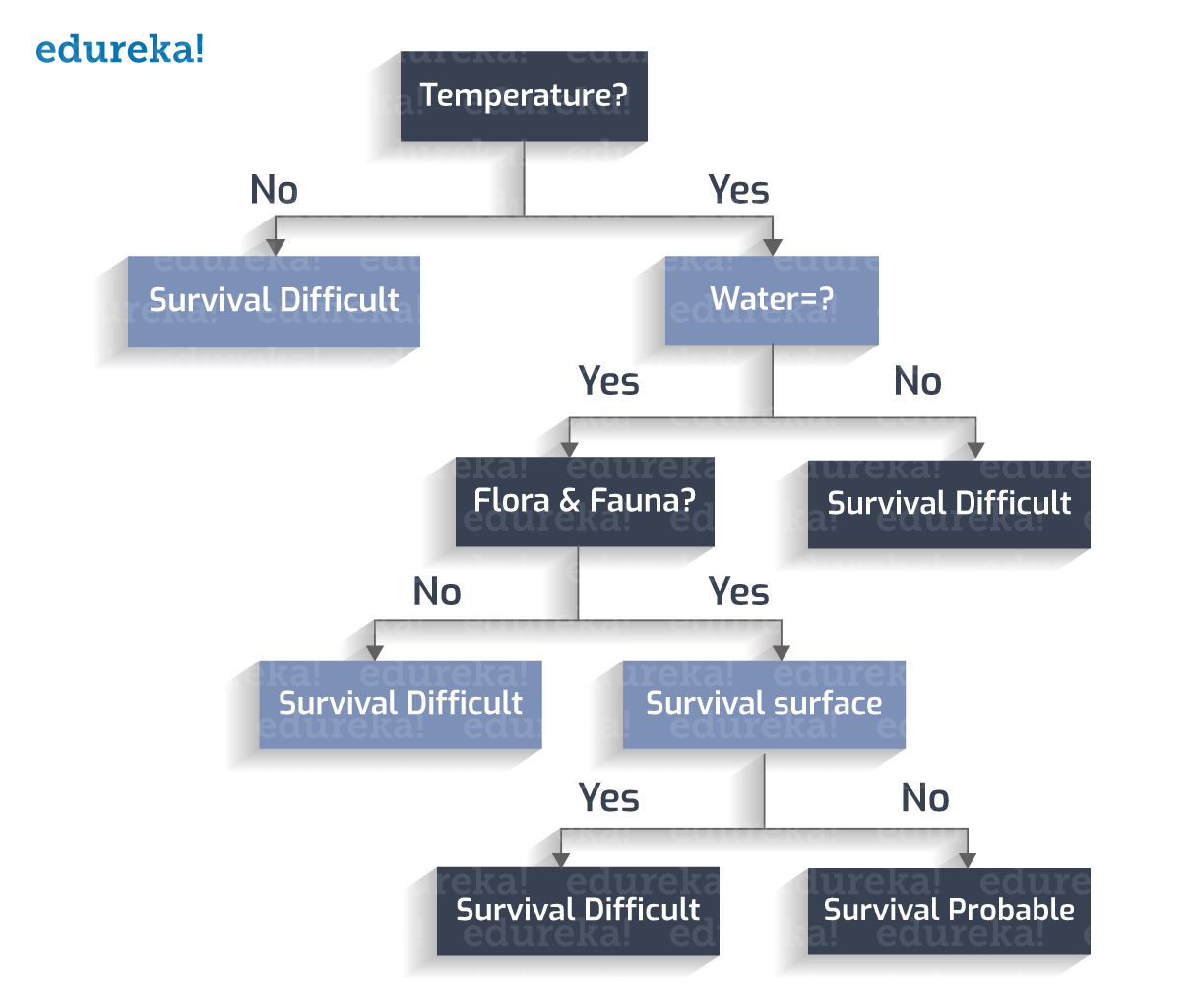
因此,我们有一个决策树。
分类规则:
分类规则是考虑所有场景并为每个场景分配一个类变量的情况。
类变量:
每个叶节点都分配了一个类变量。类变量是导致我们做出决定的最终输出。
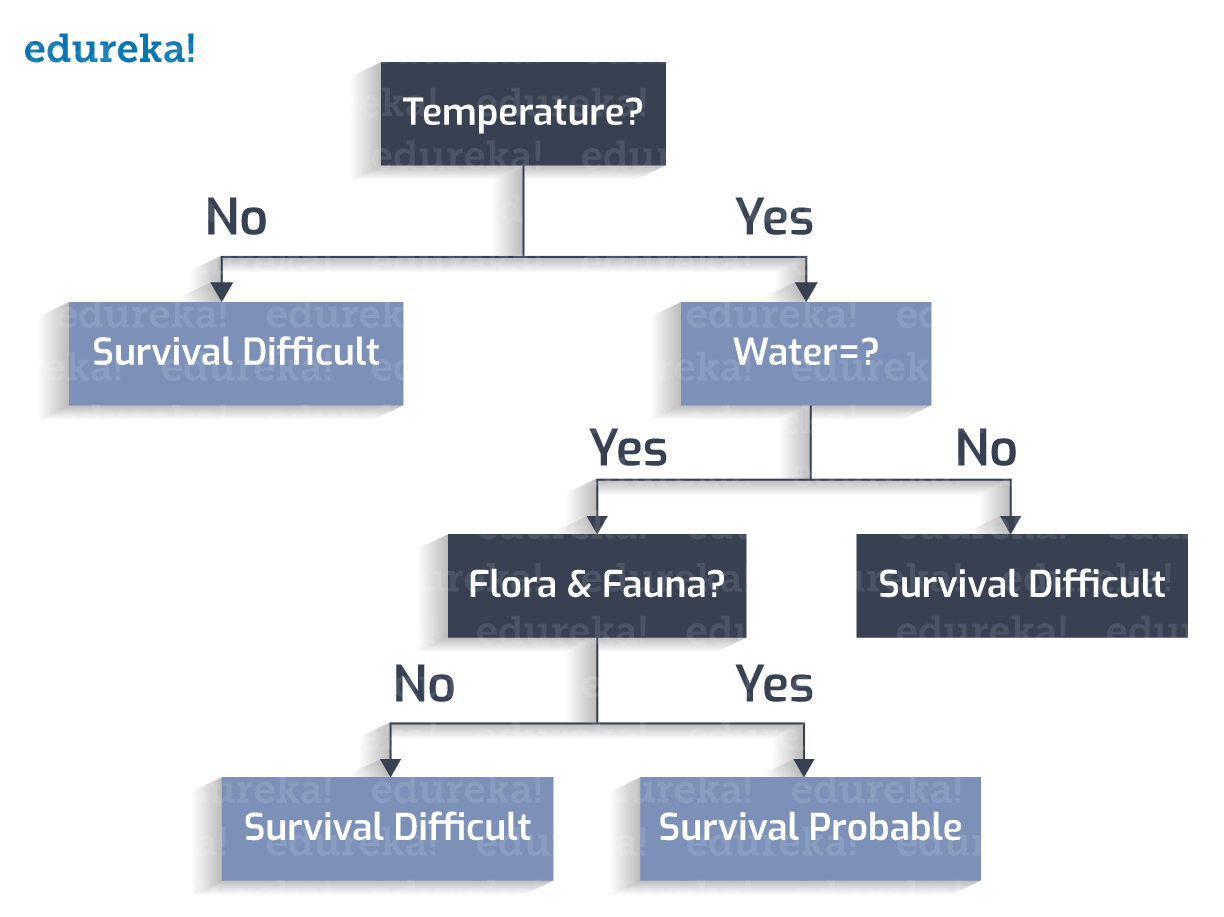
让我们从创建的决策树中推导出分类规则:
1. 如果温度不在 273 到 373K 之间,-> 生存困难
2. 如果温度在 273 到 373K 之间,并且没有水,-> 生存困难
3. 如果温度在 273 到 373K 之间,则存在水,并且不存在动植物 -> 生存困难
4. 如果温度在 273 到 373K 之间,存在水,存在动植物群,并且不存在暴风雨的表面 -> 可能生存
5. 如果温度在 273 到 373K 之间,存在水,存在动植物群,并且存在暴风雨表面 -> 生存困难
决策树
决策树具有以下组成部分:
- 根节点:在这种情况下,“温度”因素被视为根。
- 内部节点:具有一条入边和两条或更多条出边的节点。
- 叶节点:这是没有出边的终端节点。
由于决策树现在已构建,从根节点开始,我们检查测试条件并将控制分配给输出边之一,因此再次测试条件并分配节点。当所有的测试条件都指向一个叶节点时,就说决策树是完整的。叶节点包含类标签,它们对决定投赞成票或反对票。
现在,您可能会想为什么我们从根的“温度”属性开始?如果选择任何其他属性,构建的决策树将有所不同。
正确的。对于一组特定的属性,可以创建许多不同的树。我们需要通过遵循算法方法来选择最佳树。我们现在将看到创建完美决策树的“贪婪方法”。
贪婪的方法
“贪婪方法基于启发式问题解决的概念,通过在每个节点做出最佳局部选择。通过做出这些局部最优选择,我们可以在全局范围内达到近似最优解。”
该算法可以概括为:
1. 在每个阶段(节点),挑出最好的特征作为测试条件。
2. 现在将节点拆分为可能的结果(内部节点)。
3. 重复上述步骤,直到所有的测试条件都被耗尽到叶子节点中。
当您开始实现算法时,第一个问题是:“如何选择开始测试条件?”
这个问题的答案在于“熵”和“信息增益”的值。让我们看看它们是什么以及它们如何影响我们的决策树创建。
熵: 决策树中的熵代表同质性。如果数据完全同质,则熵为 0,否则如果数据被除 (50-50%),则熵为 1。
信息增益: 信息增益是节点分裂时熵值的减少/增加。
一个属性应该有最高的信息增益被选择用于分裂。根据熵和信息增益的计算值,我们在任何特定步骤选择最佳属性。
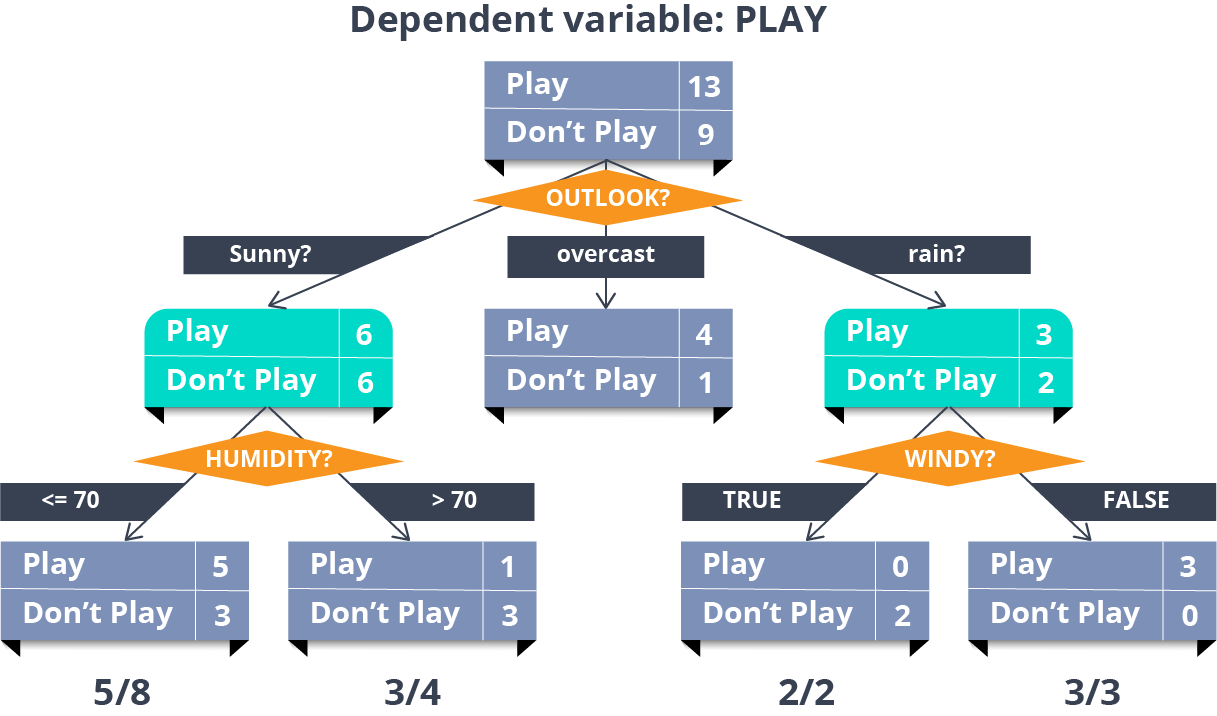
让我们考虑以下数据:
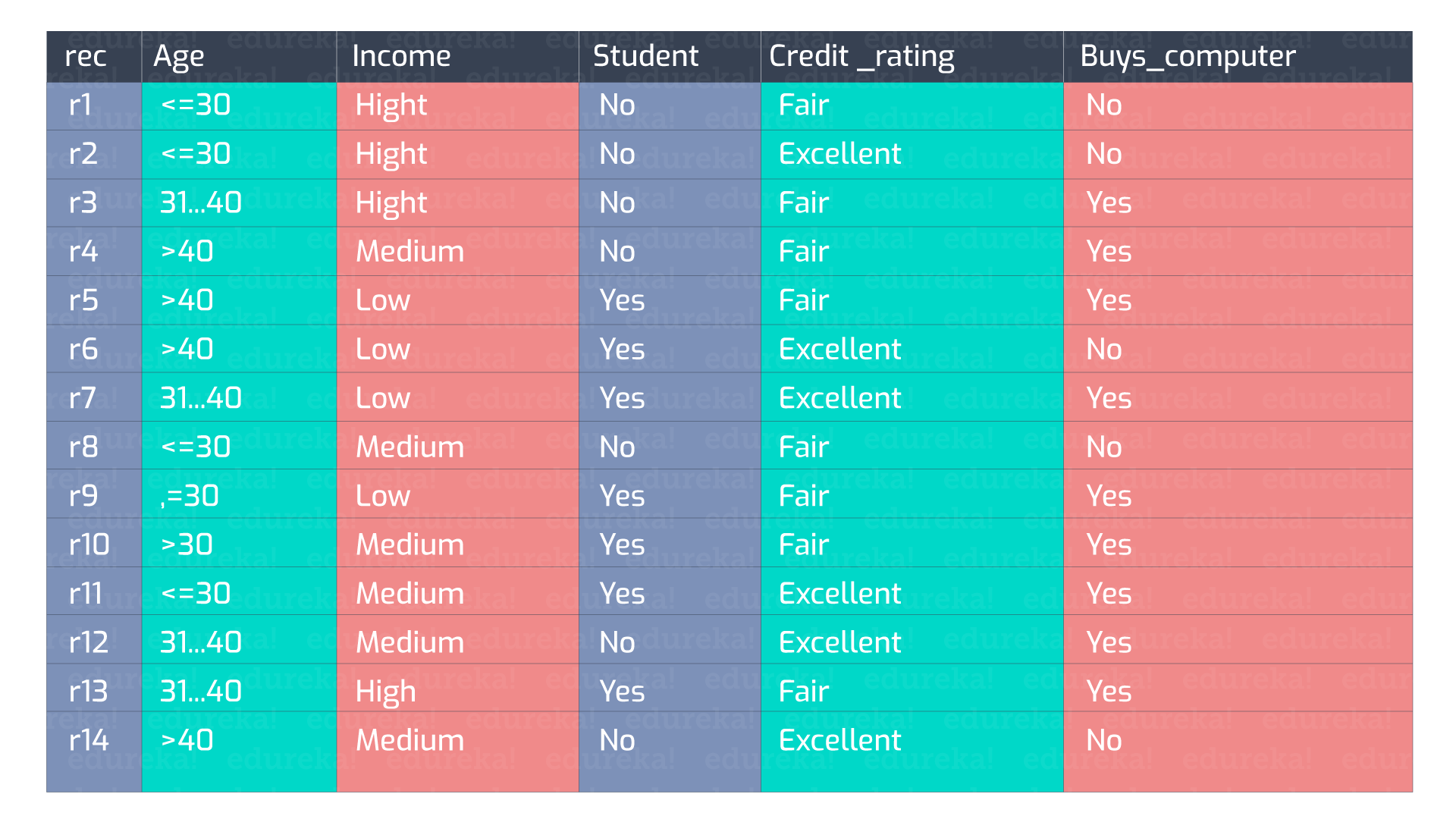
可以从这些属性集制定 n 个决策树。
树创建试验-1:
这里我们将属性“Student”作为初始测试条件。
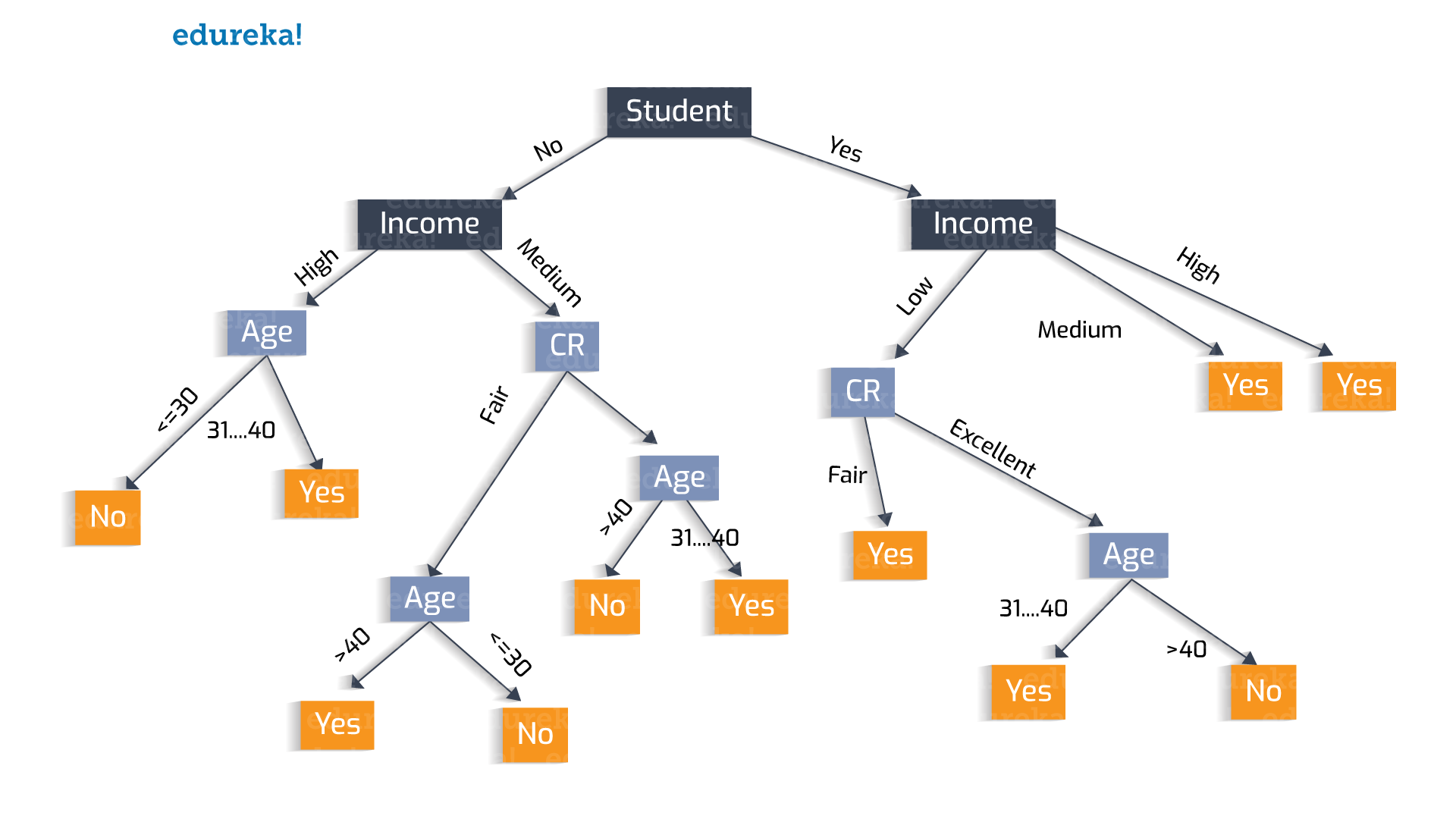
树创建试验-2:
同样,为什么选择“学生”?我们可以选择“收入”作为测试条件。
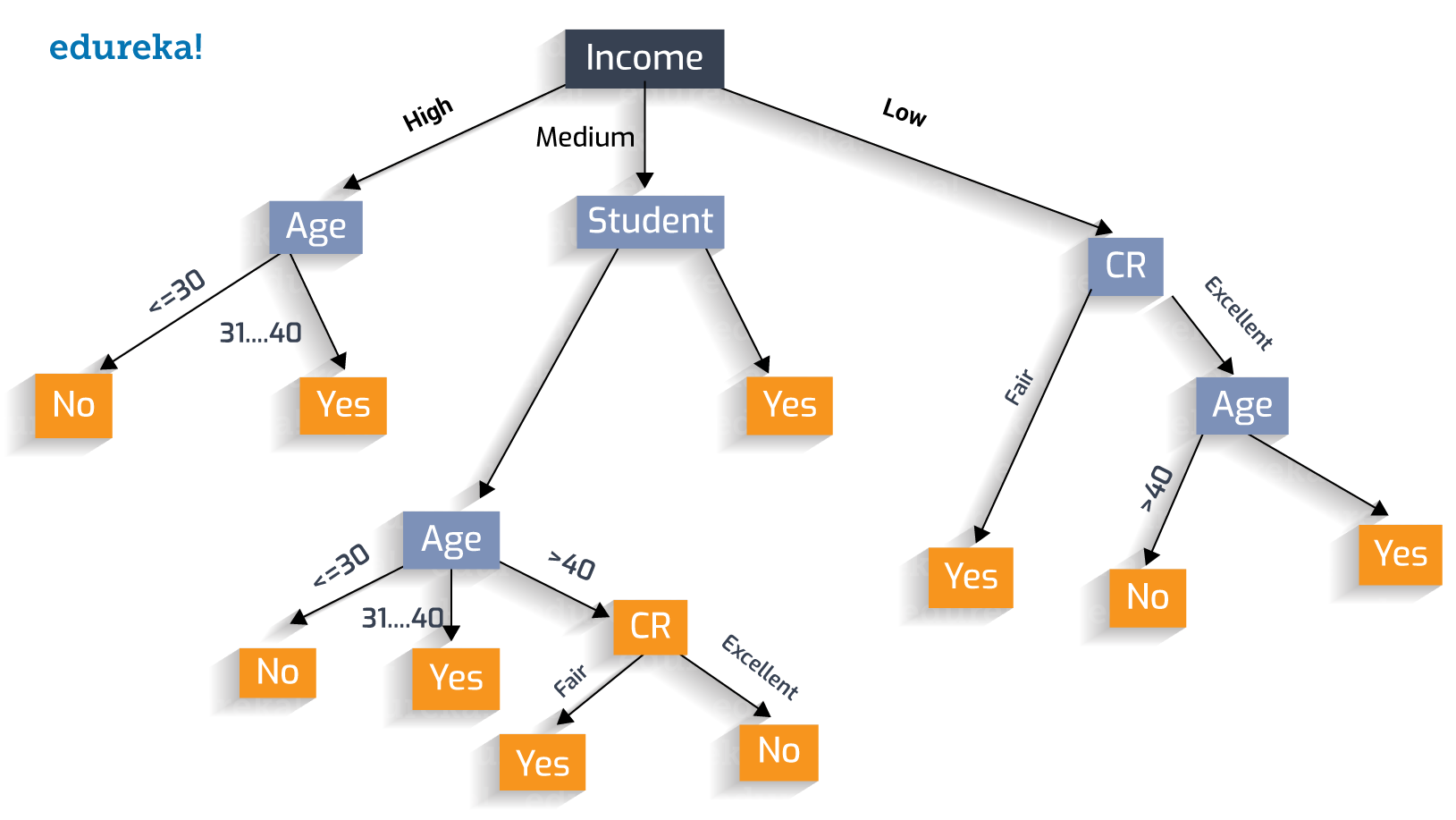
用贪心方法创建完美的决策树
让我们遵循“贪婪方法”并构建最优决策树。

D 中的熵:我们现在通过将概率值放入上述公式来计算熵。

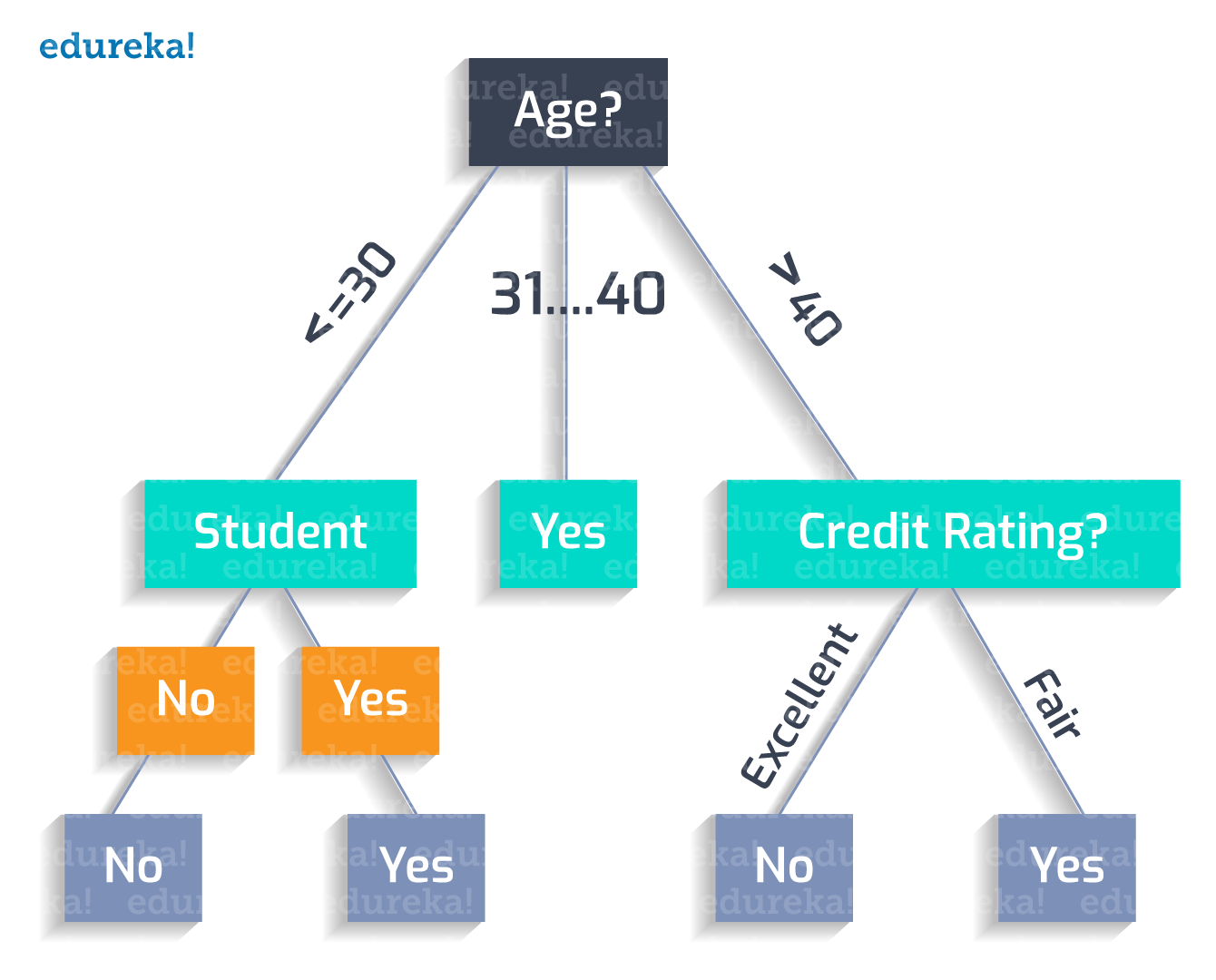
年龄(<30) ^ 学生(否) = 否
如果一个人的年龄小于 30 并且他是学生,他会购买该产品。
年龄(<30) ^ 学生(是) = 是
如果一个人的年龄在 31 到 40 岁之间,他最有可能购买。
年龄(31…40) = 是
如果一个人的年龄大于 40 岁,并且信用等级非常好,他就不会购买。
年龄(>40) ^ credit_rating(优秀) = NO
如果一个人的年龄大于 40 岁,信用等级一般,他很可能会购买。
年龄(>40) ^ credit_rating(fair) = 是
因此,我们实现了完美的决策树!!
- 点赞
- 收藏
- 关注作者


评论(0)