树

树是一种可以递归定义的数据结构

树是由n个节点组成的集合

• n=0 空树
• n>0 一个根节点，其他节点分为m个集合，每个集合本身又是一棵树

一些概念

• 根节点，叶子节点
• 树的深度（高度）
• 树的度
• 孩子节点、父节点
• 子树

二叉树

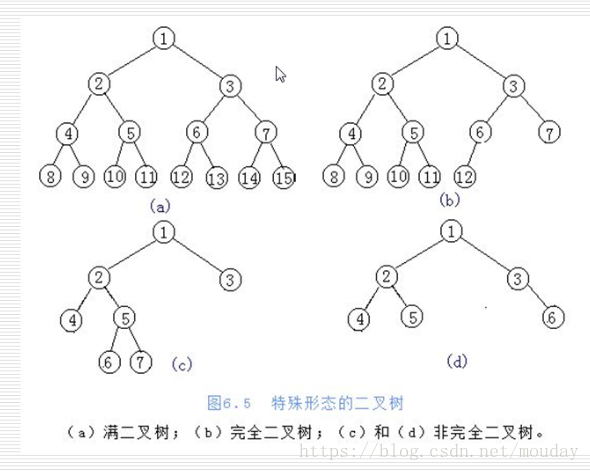
• 度不超过2的树（节点最多有两个叉）特殊的树
• 满二叉树
• 完全二叉树
  

二叉树的存储方式

• 链式存储
• 顺序存储

父节点和左孩子节点编号关系： i -> 2i+1
父节点和右孩子节点编号关系： i -> 2i+2

堆排序

堆

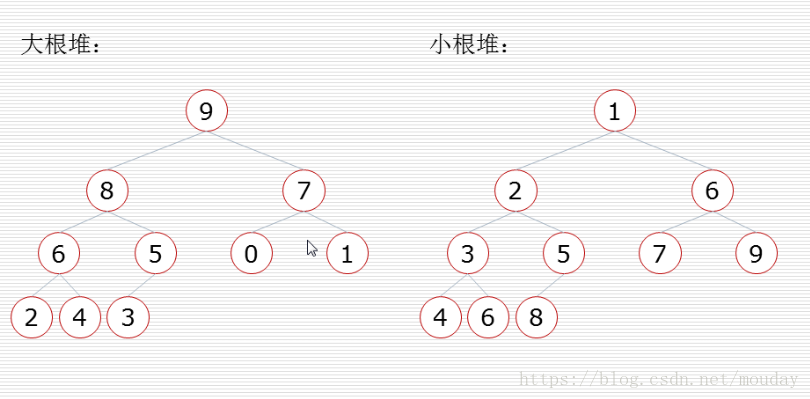
• 特殊的完全二叉树
• 大根堆：任一节点都比其孩子节点大
• 小根堆：任一节点都比其孩子节点小

调整

堆排序过程

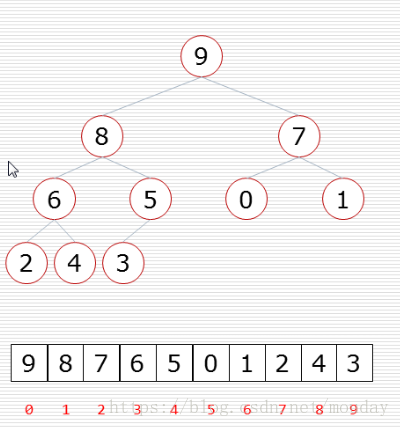
1. 建立堆
2. 得到堆顶元素，为最大元素
3. 去掉堆顶，将堆最后一个元素放到堆顶，此时可以通过一次调整重新使堆有序
4. 堆顶元素为第二大元素
5. 重复步骤3，直到堆变空
   

代码实现

import random

# 调整
def sift(lst, low, high): child = 2 * low + 1  # 左孩子 tmp = lst[low] while child < high:  # 孩子在堆里 # 如果有右孩子且比左孩子大（找到左右孩子中较大的那个） if child + 1 <= high and lst[child] < lst[child+1]: child += 1  # 孩子指向右孩子 # 孩子比父节点大 if lst[child] > tmp: lst[low] = lst[child]  # 孩子调整到父节点上 low = child  # 孩子成为新的父节点点 child = 2 * low + 1  # 新的孩子节点 else: break lst[low] = tmp  # 根节点放到父亲位置

# 堆排序
def heap_sort(lst): n = len(lst)  # 列表总长度，也就是最后一个值 for i in range(n//2 - 1, -1, -1): sift(lst, i, n-1) # i指向堆的最后 for i in range(n-1, -1, -1): # 根节点取出，最后一个孩子上位 lst[0], lst[i] = lst[i], lst[0] sift(lst, 0, i-1)  # 调整出新根节点

lst = list(range(10))
random.shuffle(lst)
heap_sort(lst)
print(lst)
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
 

文章来源: pengshiyu.blog.csdn.net，作者：彭世瑜，版权归原作者所有，如需转载，请联系作者。

原文链接：pengshiyu.blog.csdn.net/article/details/80686676