Java笔记:二进制与Java中的基本数据类型
二进制与Java中的基本数据类型
简介
二进制 0 1
逢二进一
二进制优点:
- 技术容易实现:高电压1,低电压0
- 传输可靠性高
- 适合逻辑运算:真1,假0
- 运算规则简单
二进制的缺点:
- 表示数时位数太多
- 可读性差,难于记忆
- 存储空间占用多
- 逻辑只能表示是或否
课程内容
二进制基础:
- 计算规则
- 进制转换
数据的存储
- 整型
- 浮点型
- 字符型
- 布尔型
位值制计数法
- 数码:使用的数字符号
- 基数:每个进制的基数
- 位权:固定位置对应的单位值
例如
十进制:
数码:0、1、2、3、4、5、6、7、8、9
基数:10
位权:个、十、百、千、万...
二进制:
数码:0、1
基数:2
位权:从右往左:2^0、2^1、2^2...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
二进制转化为十进制
转换规则:展开位权进行求和运算
100 =>
1*2^2 + 0*2^1 + 0*2^0 = 4
- 1
- 2
十进制转化为二进制
整数转换规则:除2取余直至运算结果为0,将余数倒序排列
十进制转二进制
29/2=14 # 1
14/2=7 # 0
7/2=3 # 1
3/2=1 # 1
1/2=0 # 1
29 => 11101
二进制转十进制
11101
= 1 * 2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0
= 16 + 8 + 4 + 1
=29
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
小数转换规则: 小数部分乘以2,直至小数点后为0,取整数部分正序排列
十进制转二进制
0.125 * 2 = 0.250 # 0
0.25 * 2 = 0.50 # 0
0.5 * 2 = 1.0 # 1
0.125 => 0.001
二进制转十进制
0.001
= 0 * 2^(-1) + 0 * 2^(-2) + 1 * 2^(-3)
= 2^(-3)
= 1/8
= 0.125
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
十进制转二进制无限循环特列
0.85 * 2 = 1.7
0.7 * 2 = 1.4
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4
0.4 * 2 = 0.8
...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
Java中的进制
八进制 0-7 八进制1位对二进制3位
十六进制 0-9 A-E 十六进制1位对二进制4位
JDK:
0b 0B 0x 0X 前缀是0,字母不区分大小写
底层存储都是二进制
输出都是十进制形式
二进制 int bin = 0b1100;
八进制 int otc = 0142;
十进制 int dec = 98;
十六进制 int hex = 0x142;
- 1
- 2
- 3
- 4
进制转换的方法
// 十进制转其他进制
Integer.toBinaryString()
Integer.toOctalString()
Integer.toHexString()
// 自定义进制
Integer.toString(int i, int radix)
// 其他进制转十进制
int Integer.parseInt(String s, int radix)
Integer Integer.valueOf(String s, int radix)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
代码示例
package com.demo.number;
public class NumberConvert { public static void main(String[] args) { int bin = 0b1100; int oct = 014; int dec = 12; int hex = 0xC; //输出都是十进制形式 System.out.println(bin); // 12 System.out.println(oct); // 12 System.out.println(dec); // 12 System.out.println(hex); // 12 // 自定义输出进制形式 System.out.println(Integer.toBinaryString(bin)); // 1100 System.out.println(Integer.toOctalString(oct)); // 14 System.out.println(Integer.toHexString(hex)); // c System.out.println(Integer.toString(dec, 10)); // 12 // 其他进制转十进制 System.out.println(Integer.parseInt("1100", 2)); // 12 System.out.println(Integer.valueOf("1100", 2)); // 12 }
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
位运算
位运算:直接对整数在内存中的二进制位进行操作
比特bit 信息量的最小单位,单位是b
字节byte 表示信息的最小单位,单位是B
1 byte = 8 bit
- 1
机器数
符号数字化 0为正,1为负
数的大小受机器字长限制
机器数的形式:原码、反码、补码
补码计算方式
正数:补码=反码=原码
负数:补码=反码+1
- 1
- 2
例如
负数相加
(-1) + (-5)
原码= 1000 0001 + 1000 0101
反码= 1111 1110 + 1111 1010
补码= 1111 1111 + 1111 1011 1111 1111
+ 1111 1011
-----------
11111 1010
舍弃溢出位
补码=1111 1010
反码=1000 0101
原码=1000 0110
= -6
正负相加
+1 + (-1)
原码=0000 0001 + 1000 0001
反码=0000 0001 + 1111 1110
补码=0000 0001 + 1111 1111 0000 0001
+ 1111 1111
------------
10000 0000
补码=0000 0000
反码=0000 0000
原码=0000 0000
=0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
位运算
| 运算名称 | 符号 | 规则 | 特点 |
|---|---|---|---|
| 按位与 | & | 清零特定位,获取特定位 | |
| 按位或 | | |
特定位替换为1 | |
| 按位异或 | ^ | 自身异或得到0,同一个数连续异或得到自身 | |
| 按位取反 | ~ | ||
| 左移 | << | 符号位不变,右侧低位补0,左侧高位舍弃 | 等价于乘以2的n次方 |
| 右移 | >> | 符号位不变,右侧低位舍弃,左侧高位正数补0,负数补1 | 等价于除以2的n次方 |
| 无符号右移 | >>> | 右侧低位舍弃,左侧高位补0 |
Java中的整数类型
整数类型使用补码存储
| 类型 | 字节数 | 最小值 | 最大值 |
|---|---|---|---|
| byte | 1字节 | -128(2^7) | +127 |
| short | 2字节 | -32768 | +32767 |
| int | 4字节 | -2147483648 | +2147483647 |
| long | 8字节 | -9223372036854775808 | +9223372036854775807 |
多字节数据的大端模式与小端模式
大端:高位字节放在低地址,低位字节放在高地址(默认)
小端:低位字节放在低地址,高位字节放在高地址
大数类BigInteger
可以存储理论无限大的整数
BigInteger(String val) 十进制字符串转BigInteger
BigInteger(String val, int radix) 指定进制字符串转BigInteger
BigInteger.valueOf(long val) 指定long转BigInteger
- 1
- 2
- 3
代码实例
package com.demo.number;
import java.math.BigInteger;
public class BigIntegerDemo { public static void main(String[] args) { BigInteger dec = new BigInteger("10"); BigInteger bin = new BigInteger("1010", 2); BigInteger lon = BigInteger.valueOf(10L); System.out.println(dec); // 10 System.out.println(bin.toString(2)); // 1010 System.out.println(lon); // 10 // 执行加法运算 System.out.println(dec.add(bin)); }
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
小数的二进制化
定点数与浮点数
指数规则:任意实数,都可以由一个定点数x基数的整数次幂得到
定点数部分:尾数,指数部分:阶码
逻辑上采用(符号位S,阶码E,尾数M)来表示一个数
IEEE754二进制浮点数标准
单精度float(4字节)1个符号位+8位阶码+23位尾数
双精度double(8字节)1个符号位+11位阶码+52位尾数
规约形式:科学计数表示法下,小数最高有效位是1(整数部分)
尾数M的表示范围:0<=M<1
规约形式实值 = 1 + M
浮点数的阶码通常用移码表示
移码:将数值正向偏移(2^(e-1)),等于符号位取反的补码
阶码:用移码(标准移码-1)记录指数,实际偏移值为(2^(e-1) - 1)
格式化的浮点数
实际值计算规则
float32位
1 01111110 01000000000000000000000
= (-1)^S * (1+M) * 2^(E-127)
= -1 * (0.01 + 1) * 2^(126-127)
= -1 * 1.25 * 2^(-1)
= -0.625
- 1
- 2
- 3
- 4
- 5
- 6
特殊值
无穷大,正负0 NaN
精确小数BigDecimal
BigDecimal(String val)
BigDecimal(Double val) // 不推荐
- 1
- 2
代码示例
package com.demo.number;
import java.math.BigDecimal;
import java.math.MathContext;
import java.math.RoundingMode;
public class BigDecimalDemo { public static void main(String[] args) { BigDecimal b1 = new BigDecimal("0.01"); BigDecimal b2 = new BigDecimal(0.01D); // 不推荐 System.out.println(b1); // 0.01 System.out.println(b2); // 0.01000000000000000020816681711721685132943093776702880859375 // 计算 BigDecimal b3 = new BigDecimal("0.1"); BigDecimal b4 = new BigDecimal("0.3"); System.out.println(b4.divide(b3)); // 3 // 遇到除不尽的情况需要设置保留精度和进位方式:四舍五入 System.out.println(b3.divide(b4, new MathContext(5, RoundingMode.HALF_UP))); // 0.33333 }
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
字符型和布尔型
字符集:字库表,编码字符集,字符编码
字库表:a、b、c…
编码字符集(码点):97、98、99…
字符编码(码元):0110 0001、0110 0010、0110 0011…
ASCII编码 128种字符信息
Unicode字符集(万国码)只有字库表和编码字符集,没有规定字符编码
字符编码:UTF-4、UTF-8、UTF-16、UTF-32
char(2字节)
使用Unicode字符集UTF-16
只能表示Unicode字符集编号65536以内的字符
大写A-Z 65-90
小写a-z 97-122
数字0-9 48-57
boolean(4个字节)
存储空间和执行效率上做取舍
处理器大多数是32位
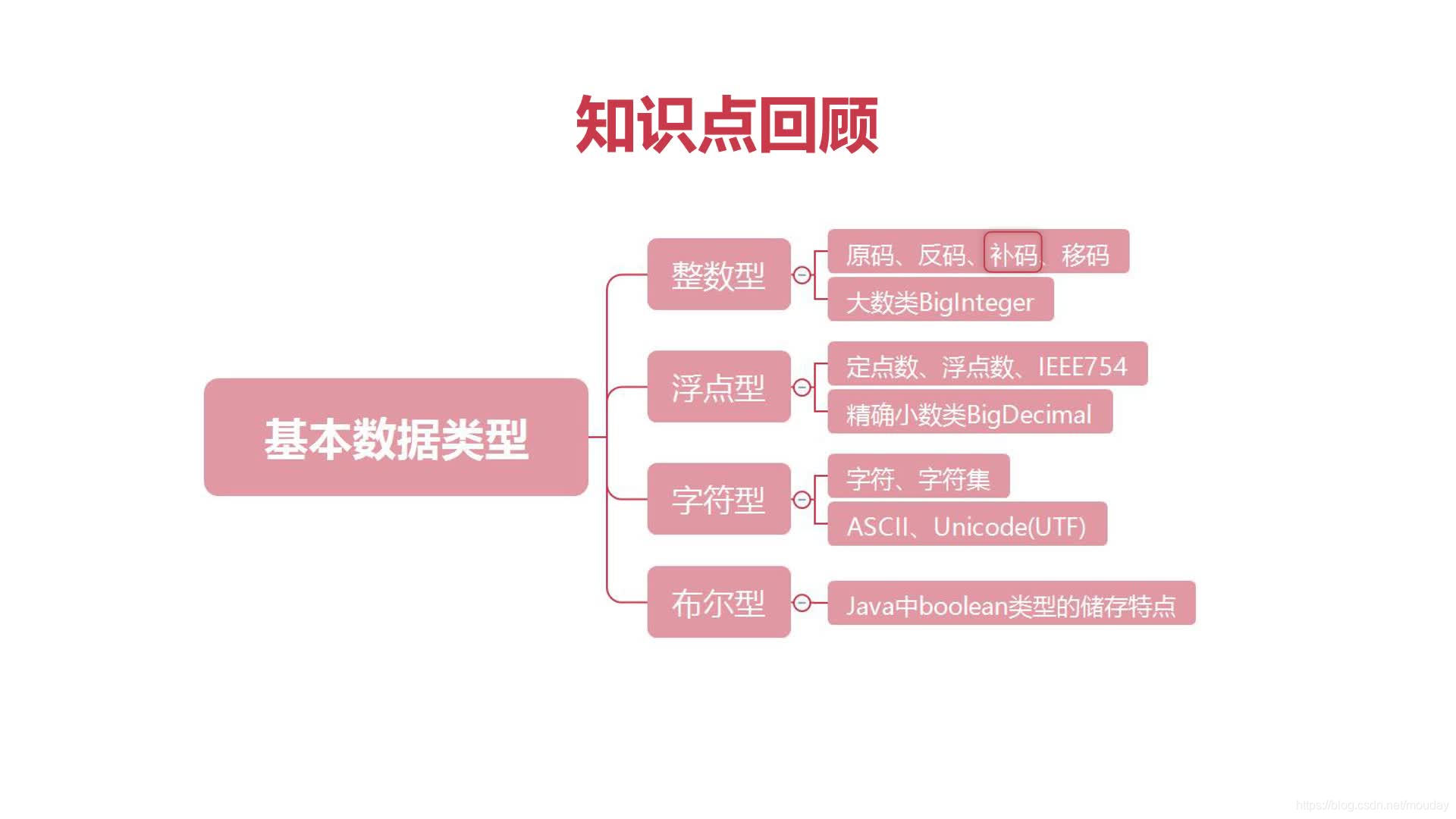
知识回顾
二进制
位值制计数法,八进制与十六进制
进制之间转换(十进制转二进制大多是无限循环)
二进制特殊运算方式:位运算
文章来源: pengshiyu.blog.csdn.net,作者:彭世瑜,版权归原作者所有,如需转载,请联系作者。
原文链接:pengshiyu.blog.csdn.net/article/details/109149835
- 点赞
- 收藏
- 关注作者


评论(0)