目录

前言

霍金先生的伟大，我无法想象，它的技术成就，我亦不配评论。但霍金先生对抗病魔的精神，就值得我由衷敬佩。尽自己的能力写好该系列，以此缅怀霍金先生。

排列数公式推导证明

定义：从 n 个不同元素的集合中，任意取出 m(m<=n) 个元素排成一列（有先后顺序）称为一个排列；此种排列的总数即为排列数，即叫做从 n 个不同元素中取出 m 和元素的排列数。

公式：

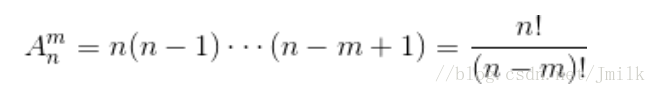
（当 n=m 时，分母为 0! = 1，即为全排列）

推导：在具有 n 个数的集合中，顺序取出 m 个数，成为一个排列。

• 取出第 1 个数，有 n 种选法
• 取出第 2 个数，有 n-1 种选法
• …
• 取出第 m 个数，有 n-m+1 种选法
• …
• 最后一个数，只有 1 中选法

上述过程符合「分步乘法计数」场景，应用分步乘法计数公式：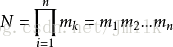

得到 n(n-1)(n-2)…(n-m+1)，即 A(n, m) = n! / (n-m)! 。

组合数公式推导证明

定义：从 n 个不同元素的集合中，任意取出 m(m<=n) 个元素并成一组（无先后顺序），叫做从 n 个不同元素中取出 m 个元素的一个组合；从 n 个不同元素的集合中取出 m(m<=n) 个元素的所有组合的个数，叫做从 n 个不同元素中取出 m 个元素的组合数。

公式：

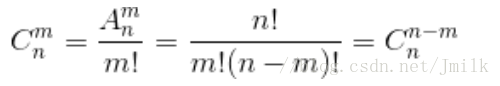
推导：在具有 n 个数的集合中，获取 m 个数组成一组。
首先依旧可以得到排列数 A(n, m)，但又因为组合数是无序的，而排列数是有序的，所以需要在 A(n, m) 的基础上去除掉元素组合一致的排列。即 C(n, m) = A(n, m) / m! 。这里的理解需要转一下弯，所以我们通过下述证明来辅助理解这条公式。

证明：A(n, m) = C(n, m) * A(m, m)
第一步，从 n 个球中取出 m 个来，先不排序，所以为组合数问题，得到 C(n, m)。
第二步，将第一步取出的球全部排列，A(m, m) = m!，即求组合的全排列。
第三步，应用分步乘法计数原理，得到 A(n, m) = C(n, m) * A(m, m)，即 A(n, m) = C(n, m) * m! 得证。

所以从 n 中取出 m 的排列数，实际为从 n 中取出 m 的组合数与每一个组合自身所拥有的全排列数的乘积。

重复组合数公式推导证明

定义：重复组合是一种特殊的组合，从 n 个不同元素的集合中允许重复地取出 m 个元素（任意取出一个元素，然后再将其放回到集合中）形成一个组合，叫做从 n 个元素中取出 m 个元素的重复组合。

公式:

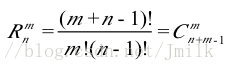
分析（放球模型）：将重复组合的概念转换为放球模型来进行分析，将 n 个不同的元素当作 n 个不同的格子，既有 n-1 块相同的隔板。同时用 m 个相同的小球，当作取出 m 个元素。现在问将 m 个相同的小球放到 n 个格子里，有多少种方法？

相当于：

• 先求 m 个小球和 n-1 块隔板所组成的集合 (m+n-1) 的全排列。
• 又因为 m 个小球是相同的，n-1 块隔板亦是相同的，所以需要除以重复的情况 C(m, m) * C(n-1, n-1) = m! * (n-1)! 。
• 所以最终使用全排列数除以重复的次数，得到重复组合数 (m+n-1)! / m! * (n-1)!，即 C(m+n-1, m) 。

组合数恒等公式

最后再给出组合数恒等公式，大家不妨自己推导一下吧。

文章来源: is-cloud.blog.csdn.net，作者：范桂飓，版权归原作者所有，如需转载，请联系作者。

原文链接：is-cloud.blog.csdn.net/article/details/79563285