用 C 语言开发一门编程语言 — 抽象语法树

举报
云物互联 发表于 2021/08/05 23:57:29 2021/08/05
【摘要】 目录 文章目录 目录前文列表抽象语法树的结构使用递归来遍历树结构实现求值计算 抽象语法树与行为树 前文列表 《用 C 语言开发一门编程语言 — 交互式解析器l》 《用 C 语言开发一门编程语言 — 跨平台的可移植性》 《用 C 语言开发一门编程语言 — 语法解析器》 抽象语法树的结构 lispy> + 5 (* 2 2) > r...

目录

文章目录

前文列表

《用 C 语言开发一门编程语言 — 交互式解析器l》
《用 C 语言开发一门编程语言 — 跨平台的可移植性》
《用 C 语言开发一门编程语言 — 语法解析器》

抽象语法树的结构

lispy> + 5 (* 2 2)
>
  regex
  operator|char:1:1 '+'
  expr|number|regex:1:3 '5'
  expr|> char:1:5 '(' operator|char:1:6 '*' expr|number|regex:1:8 '2' expr|number|regex:1:10 '2' char:1:11 ')'
  regex

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    •

上篇我们通过 MPC 解析器组合库完成了读取输入，对波兰表达式的语法解析并得到表达式的 AST（抽象语法树），操作数（Number）和操作符（Operator）等需要被处理的有效数据都位于叶子节点上。而非叶子节点上则包含了遍历和求值的信息。

但是现在我们仍不能对它进行计算求值。在实现计算求值之前，我们先好好看看 AST 的结构：

typedef struct mpc_ast_t {
  char *tag;
  char *contents;
  mpc_state_t state;
  int children_num;
  struct mpc_ast_t **children;
} mpc_ast_t;

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    •
  • tag：就是在节点内容之前的信息，它表示了解析这个节点时所用到的所有规则。例如：expr|number|regex。tag 字段非常重要，因为它可以让我们知道创建节点时所匹配到的规则。
  • contents：包含了节点中具体的操作数和操作符内容，例如 *、(、5。你会发现，对于表示分支的非叶子节点，这个字段为空。而对于叶子节点，则包含了操作数或操作符的字符串形式。
  • state：这里面包含了解析器发现这个节点时所处的状态，例如行数和列数等信息。本书不会用到这个字段。
  • children_num 和 children：帮助我们来遍历 AST。前一个字段告诉我们有多少个子节点，后一个字段是包含这些节点的数组。其中，children 的数据类型为 mpc_ast_t ** 二重指针类型，是一个指针数组。
/* Load AST from output。
 * 因为 mpc_ast_t* 是指向结构体的指针类型，所以获取其字段的语法有些许不同。我们需要使用 -> 符号，而不是 . 符号。
 */
mpc_ast_t *a = r.output;
printf("Tag: %s\n", a->tag);
printf("Contents: %s\n", a->contents);
printf("Number of children: %i\n", a->children_num);

/* Get First Child */
mpc_ast_t *c0 = a->children[0];
printf("First Child Tag: %s\n", c0->tag);
printf("First Child Contents: %s\n", c0->contents);
printf("First Child Number of children: %i\n",
  c0->children_num);

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    •

使用递归来遍历树结构

树形结构是自身重复的。树的每个子节点都是树，每个子节点的子节点也是树，以此类推。可见，树形结构也是递归和重复的。如果我们想编写函数处理所有可能的情况，就必须要保证函数可以处理任意深度，我们可以使用递归函数的天生优势来轻松地处理这种重复自身的结构。
在这里插入图片描述

递归函数就是在执行的过程中调用自身的函数。理论上，递归函数会无穷尽地执行下去。但实际上，递归函数对于不同的输入会产生不同的输出，如果我们每次递归都改变或使用不同的输入，并设置递归终止的条件，我们就可以使用递归实现预期的效果。例如：使用递归来计算树形结构中节点个数。

首先考虑最简单的情况，如果输入的树没有子节点，我们只需简单的返回 1 表示根节点就行了。如果输入的树有一个或多个子节点，这时返回的结果就是根节点再加上所有子节点的值。

使用递归，遍历统计子节点的数量：

int number_of_nodes(mpc_ast_t* t) {
  if (t->children_num == 0) { return 1; }
  if (t->children_num >= 1) { int total = 1; for (int i = 0; i < t->children_num; i++) { total = total + number_of_nodes(t->children[i]); } return total;
  }
}

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    •

实现求值计算

lispy> + 5 (* 2 2)
>
  regex
  operator|char:1:1 '+'
  expr|number|regex:1:3 '5'
  expr|> char:1:5 '(' operator|char:1:6 '*' expr|number|regex:1:8 '2' expr|number|regex:1:10 '2' char:1:11 ')'
  regex

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    •

在实现代码之前再好好总结一下 AST 输出的特征：

  • 有 number 标签的节点一定是一个数字，并且没有子节点。我们可以直接将其转换为一个数字。
  • 如果一个节点有 expr 标签，但没有 number 标签，那么第一个子节点永远是 ( 字符，最后一个子节点是 ) 字符。我们需要看他的第二个子节点是什么操作符，然后我们需要使用这个操作符来对后面的子节点进行求值。

在对语法树进行求值的时候，还需要保存计算的结果。在这里，我们使用 C 语言中 long 类型。另外，为了检测节点的类型，或是为了获得节点中保存的数值，我们会用到节点中的 tag 和 contents 字段。这些字段都是字符串类型的。

我们引入一些辅助性的库函数：

在这里插入图片描述
我们可以使用 strcmp 来检查应该使用什么操作符，并使用 strstr 来检测 tag 中是否含有某个字段：

#include <stdio.h>
#include <stdlib.h>
#include "mpc.h"

#ifdef _WIN32
#include <string.h>

static char buffer[2048];

char *readline(char *prompt) { fputs(prompt, stdout); fgets(buffer, 2048, stdin); char *cpy = malloc(strlen(buffer) + 1); strcpy(cpy, buffer); cpy[strlen(cpy) - 1] = '\0'; return cpy;
}

void add_history(char *unused) {}

#else

#ifdef __linux__
#include <readline/readline.h>
#include <readline/history.h>
#endif

#ifdef __MACH__
#include <readline/readline.h>
#endif

#endif

/* Use operator string to see which operation to perform */
long eval_op(long x, char *op, long y) { if (strcmp(op, "+") == 0) { return x + y; } if (strcmp(op, "-") == 0) { return x - y; } if (strcmp(op, "*") == 0) { return x * y; } if (strcmp(op, "/") == 0) { return x / y; } return 0;
}

long eval(mpc_ast_t *t) { /* If tagged as number return it directly. * 有 number 标签的节点一定是一个数字，并且没有子节点 * 直接将其转换为一个数字。 */ if (strstr(t->tag, "number")) { return atoi(t->contents); } /* The operator is always second child. * 如果一个节点有 expr 标签，但没有 number 标签，那么它的第二个子节点肯定是操作符。 * 这个操作符后面的子节点肯定是操作数。 */ char *op = t->children[1]->contents; long x = eval(t->children[2]); /* 迭代剩余的子节点，并求值。 */ int i = 3; while (strstr(t->children[i]->tag, "expr")) { x = eval_op(x, op, eval(t->children[i])); i++; } return x;
}

int main(int argc, char *argv[]) { /* Create Some Parsers */ mpc_parser_t *Number   = mpc_new("number"); mpc_parser_t *Operator = mpc_new("operator"); mpc_parser_t *Expr = mpc_new("expr"); mpc_parser_t *Lispy = mpc_new("lispy"); /* Define them with the following Language */ mpca_lang(MPCA_LANG_DEFAULT, " \ number   : /-?[0-9]+/ ; \ operator : '+' | '-' | '*' | '/' ; \ expr : <number> | '(' <operator> <expr>+ ')' ;  \ lispy : /^/ <operator> <expr>+ /$/ ; \ ", Number, Operator, Expr, Lispy); puts("Lispy Version 0.1"); puts("Press Ctrl+c to Exit\n"); while(1) { char *input = NULL; input = readline("lispy> "); add_history(input); /* Attempt to parse the user input */ mpc_result_t r; if (mpc_parse("<stdin>", input, Lispy, &r)) { /* On success print and delete the AST */ long result = eval(r.output); printf("%li\n", result); mpc_ast_delete(r.output); } else { /* Otherwise print and delete the Error */ mpc_err_print(r.error); mpc_err_delete(r.error); } free(input); } /* Undefine and delete our parsers */ mpc_cleanup(4, Number, Operator, Expr, Lispy); return 0;
}

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    • 
  
  • 9
    • 
  
  • 10
    • 
  
  • 11
    • 
  
  • 12
    • 
  
  • 13
    • 
  
  • 14
    • 
  
  • 15
    • 
  
  • 16
    • 
  
  • 17
    • 
  
  • 18
    • 
  
  • 19
    • 
  
  • 20
    • 
  
  • 21
    • 
  
  • 22
    • 
  
  • 23
    • 
  
  • 24
    • 
  
  • 25
    • 
  
  • 26
    • 
  
  • 27
    • 
  
  • 28
    • 
  
  • 29
    • 
  
  • 30
    • 
  
  • 31
    • 
  
  • 32
    • 
  
  • 33
    • 
  
  • 34
    • 
  
  • 35
    • 
  
  • 36
    • 
  
  • 37
    • 
  
  • 38
    • 
  
  • 39
    • 
  
  • 40
    • 
  
  • 41
    • 
  
  • 42
    • 
  
  • 43
    • 
  
  • 44
    • 
  
  • 45
    • 
  
  • 46
    • 
  
  • 47
    • 
  
  • 48
    • 
  
  • 49
    • 
  
  • 50
    • 
  
  • 51
    • 
  
  • 52
    • 
  
  • 53
    • 
  
  • 54
    • 
  
  • 55
    • 
  
  • 56
    • 
  
  • 57
    • 
  
  • 58
    • 
  
  • 59
    • 
  
  • 60
    • 
  
  • 61
    • 
  
  • 62
    • 
  
  • 63
    • 
  
  • 64
    • 
  
  • 65
    • 
  
  • 66
    • 
  
  • 67
    • 
  
  • 68
    • 
  
  • 69
    • 
  
  • 70
    • 
  
  • 71
    • 
  
  • 72
    • 
  
  • 73
    • 
  
  • 74
    • 
  
  • 75
    • 
  
  • 76
    • 
  
  • 77
    • 
  
  • 78
    • 
  
  • 79
    • 
  
  • 80
    • 
  
  • 81
    • 
  
  • 82
    • 
  
  • 83
    • 
  
  • 84
    • 
  
  • 85
    • 
  
  • 86
    • 
  
  • 87
    • 
  
  • 88
    • 
  
  • 89
    • 
  
  • 90
    • 
  
  • 91
    • 
  
  • 92
    • 
  
  • 93
    • 
  
  • 94
    • 
  
  • 95
    • 
  
  • 96
    • 
  
  • 97
    • 
  
  • 98
    • 
  
  • 99
    • 
  
  • 100
    • 
  
  • 101
    • 
  
  • 102
    • 
  
  • 103
    • 
  
  • 104
    • 
  
  • 105
    • 
  
  • 106
    • 
  
  • 107
    • 
  
  • 108
    • 
  
  • 109
    • 
  
  • 110
    • 
  
  • 111
    • 
  
  • 112
    • 
  
  • 113
    • 
  
  • 114
    • 
  
  • 115
    • 
  
  • 116
    • 
  
  • 117
    • 
  
  • 118
    • 
  
  • 119
    • 
  
  • 120
    • 
  
  • 121
    •

编译：

gcc -std=c99 -Wall parsing.c mpc.c -lreadline -lm -o parsing

  
 
    
  
  • 1
    •

运行：

$ ./parsing
Lispy Version 0.1
Press Ctrl+c to Exit

lispy> - (* 10 10) (+ 1 1 1)
97
lispy> + 5 6
11

  
 
    
  
  • 1
    • 
  
  • 2
    • 
  
  • 3
    • 
  
  • 4
    • 
  
  • 5
    • 
  
  • 6
    • 
  
  • 7
    • 
  
  • 8
    •

抽象语法树与行为树

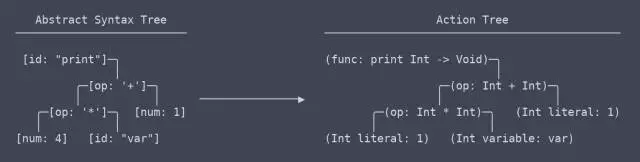
在这里插入图片描述
行为树和抽象语法树之间有一个细微但非常重要的区别，我们应该区别对待（这促成了解析器的改写）。

简单来说，行为树是带有上下文的 AST。上下文是一个函数返回的类型的信息，或者两个地方使用的变量实际上是相同的变量。 因为它需要弄清楚并记住所有这些上下文，生成行为树的代码需要大量的命名空间查找表和其他的东西。

一旦我们有了行为树，运行代码就很容易了。 每个行为节点都有一个函数 “execute”，它接受一些输入，不管行为应该如何（包括可能调用子行为），返回行为的输出。 这是行为中的解释器。

文章来源: is-cloud.blog.csdn.net，作者：范桂飓，版权归原作者所有，如需转载，请联系作者。

原文链接：is-cloud.blog.csdn.net/article/details/105386120

【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
C语言 面向对象编程
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入