MATLAB--从正弦波转换为方波(验证傅里叶级数)

从正弦波转换为方波(傅里叶验证)

此示例说明方波的傅里叶级数展开式是如何由奇次谐波的和构成的。

1.首先以 0.1 为步长，生成一个从 0 到 10 的时间向量，并求出所有点的正弦。绘制基频图

t = 0:.1:10;
y = sin(t);
plot(t,y);

  
 

  
1
  
2
  
3
 

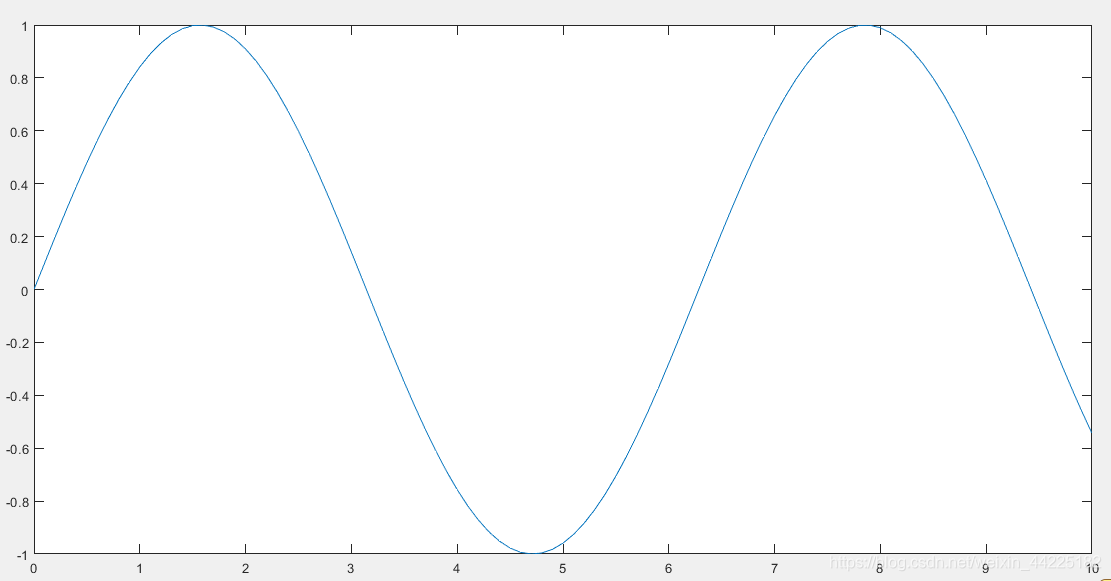
2.接下来，向基频添加第三个谐波，并绘制谐波图

y = sin(t) + sin(3*t)/3;
plot(t,y);

  
 

  
1
  
2
 

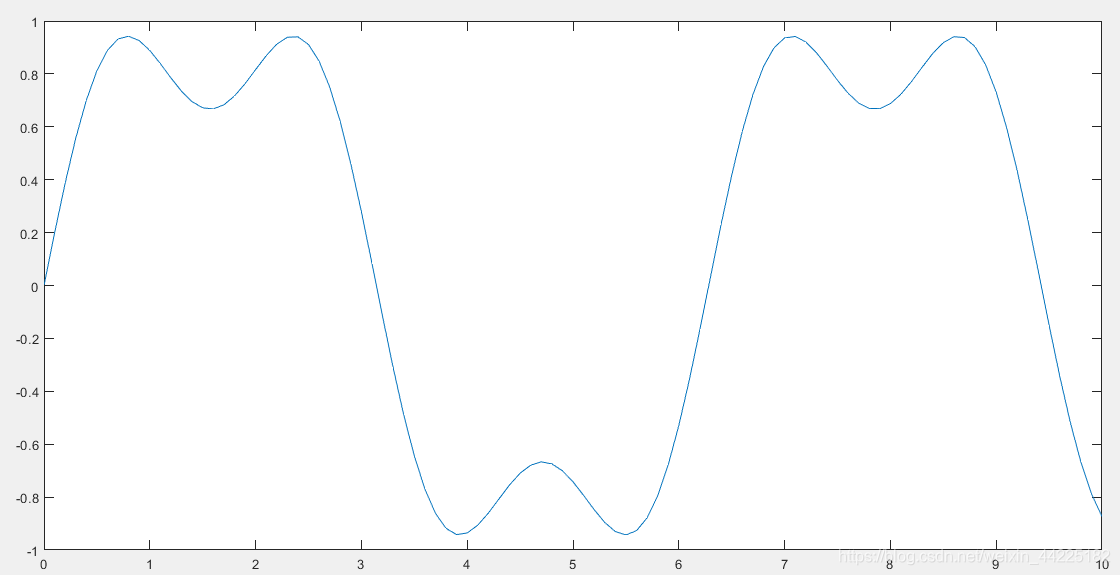
3.接下来使用第一、第三、第五、第七和第九个谐波

y = sin(t) + sin(3*t)/3 + sin(5*t)/5 + sin(7*t)/7 + sin(9*t)/9;
plot(t,y);

  
 

  
1
  
2
 

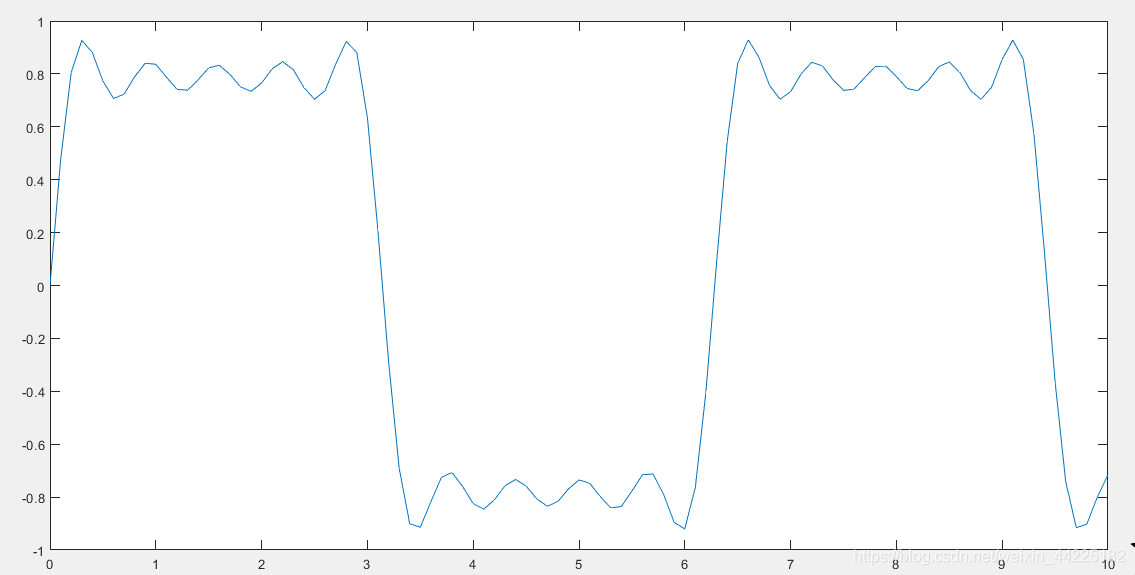
4.最后，从基频开始创建更多连续谐波的向量，一直到第 19 个谐波为止，并将所有中间步长保存为矩阵的行。

在同一个图窗中绘制这些向量，以便显示方波的演变。请注意，吉布斯效应表明它实际上永远不会转换为方波。

t = 0:.02:3.14;
y = zeros(10,length(t));
x = zeros(size(t));
for k = 1:2:19 x = x + sin(k*t)/k; y((k+1)/2,:) = x;
end
plot(y(1:2:9,:)')
title('The building of a square wave: Gibbs'' effect')

  
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
 

5.下面提供了一个三维曲面图，该曲面图表示正弦波到方波的逐变过程

surf(y);
shading interp
axis off ij

  
 

  
1
  
2
  
3
 

文章来源: haihong.blog.csdn.net，作者：海轰Pro，版权归原作者所有，如需转载，请联系作者。

原文链接：haihong.blog.csdn.net/article/details/102486298