MATLAB--运用傅里叶变换对信号进行简单的滤波

运用傅里叶变换对信号进行简单的滤波

原理
将信号进行傅里叶变换可以信号中有哪些频率成分，将需要滤除的频率成分的幅值置零，然后进行傅里叶逆变换就可以达到滤波的目的。

注意点
运行FFT进行变换时需要考虑奈奎斯特之后的振幅和相位，进行傅里叶逆变换的时候是取N个点进行变换，而不是取一半。

下面以一个实例进行说明
信号：x=0.5sin(2pi3t)+cos(2pi10*t)，滤除8Hz-12Hz的信号。

dt=0.02;%采样间隔
N=512;%采样点数
t=0:dt:(N-1)*dt;%采样时刻
fs=1/dt;%采样频率，与才采样间隔互为倒数
n=0:1:N-1;
f=(fs/N).*n;%X轴每个点对应的频率
x=0.5*sin(2*pi*3*t)+cos(2*pi*10*t);%信号
figure(1)
plot(t,x)
y=fft(x);%傅里叶变换得到一个复数
Ay=abs(y);%取模
Ayy=Ay*2/N;%转换成实际的幅值
figure(2)
plot(f(1:N/2),Ayy(1:N/2))
f1=8;
f2=15;
yy=zeros(1,length(y));
for m=0:N-1 if(m*(fs/N)>f1&m*(fs/N)&&(fs-f2)&m*(fs/N)<(fs-f1));%将奈奎斯特之后的频率也滤除点掉 yy(m+1)=0; else yy(m+1)=y(m+1); end
end %将频率为8Hz-12Hz的信号的幅值置0
yyi=abs(yy);
figure(3)
plot(f(1:N/2),yyi(1:N/2))
yi=ifft(yy);
figure(4)
plot(t,real(yi))

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
 

结果

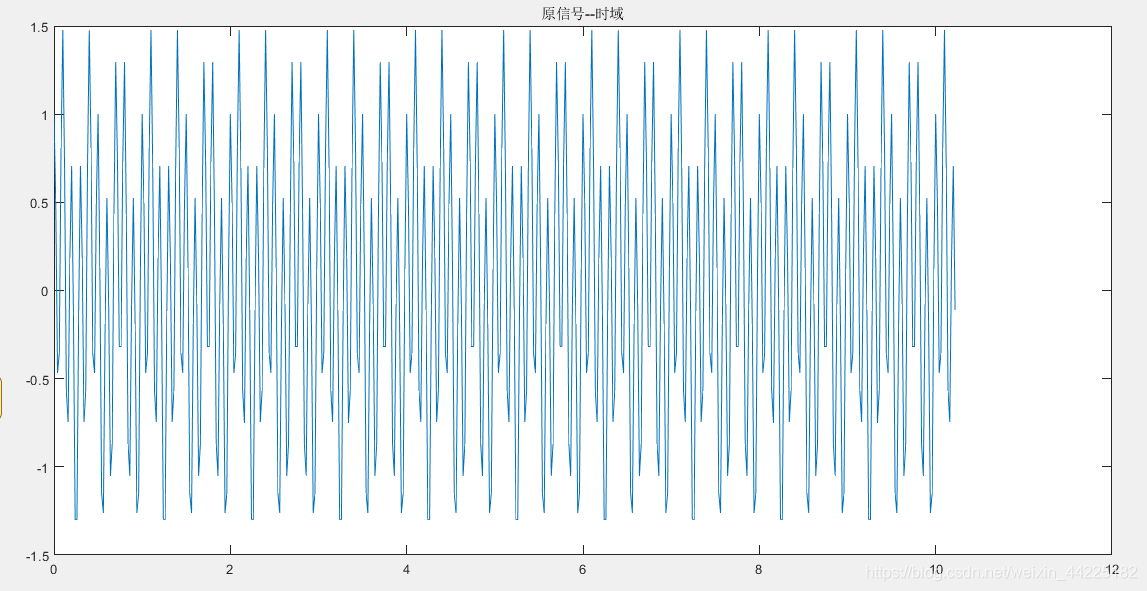
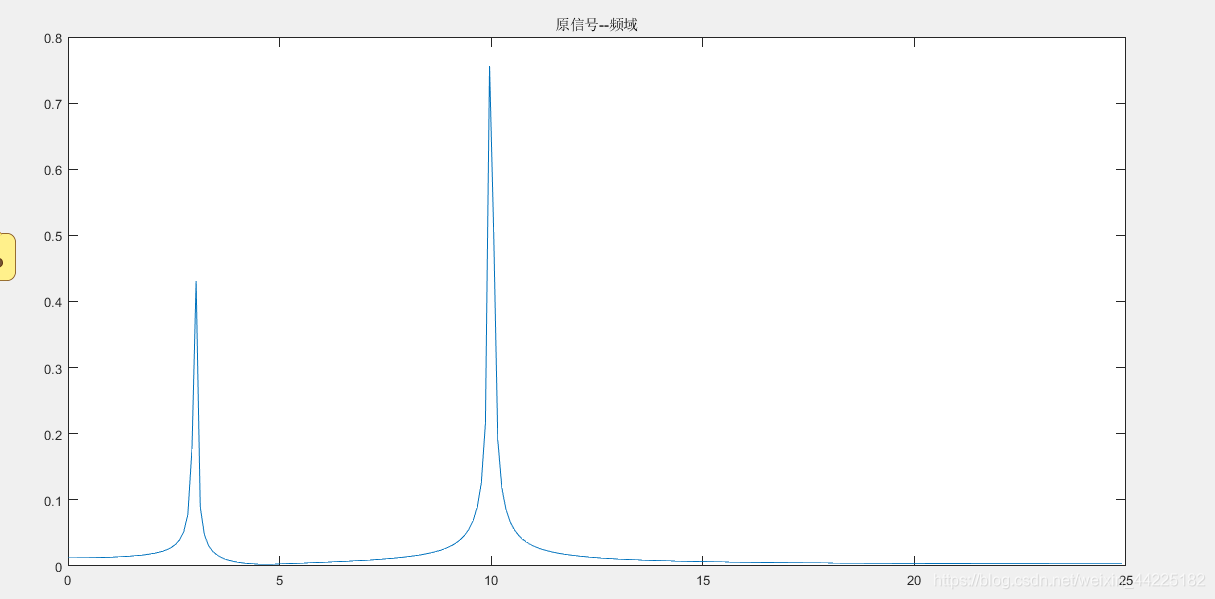
滤波后

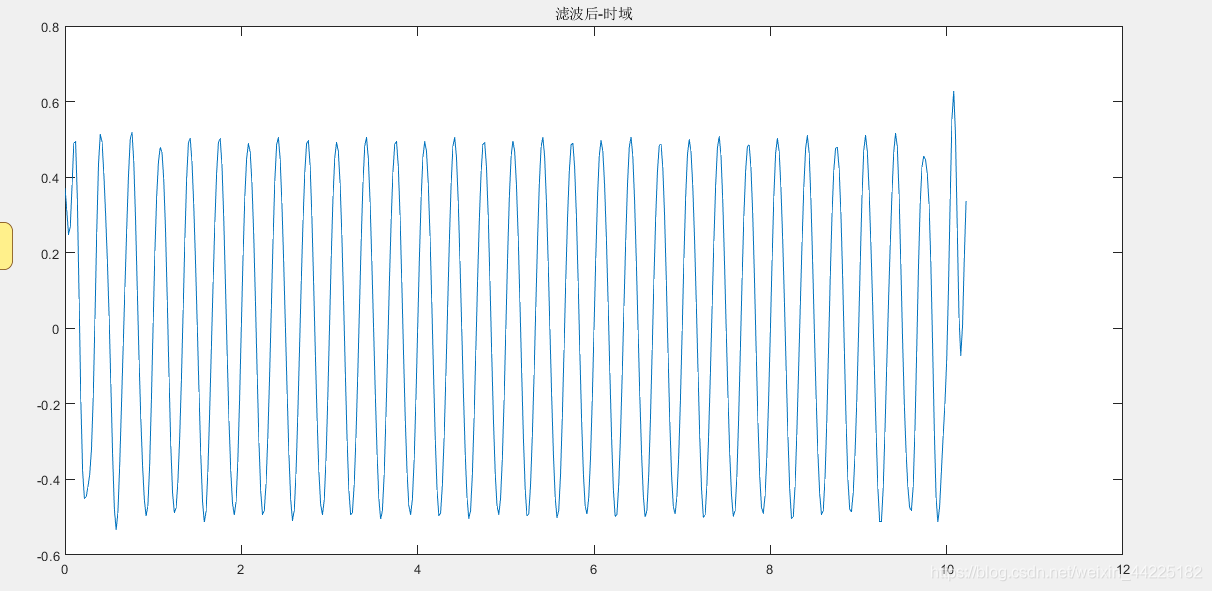
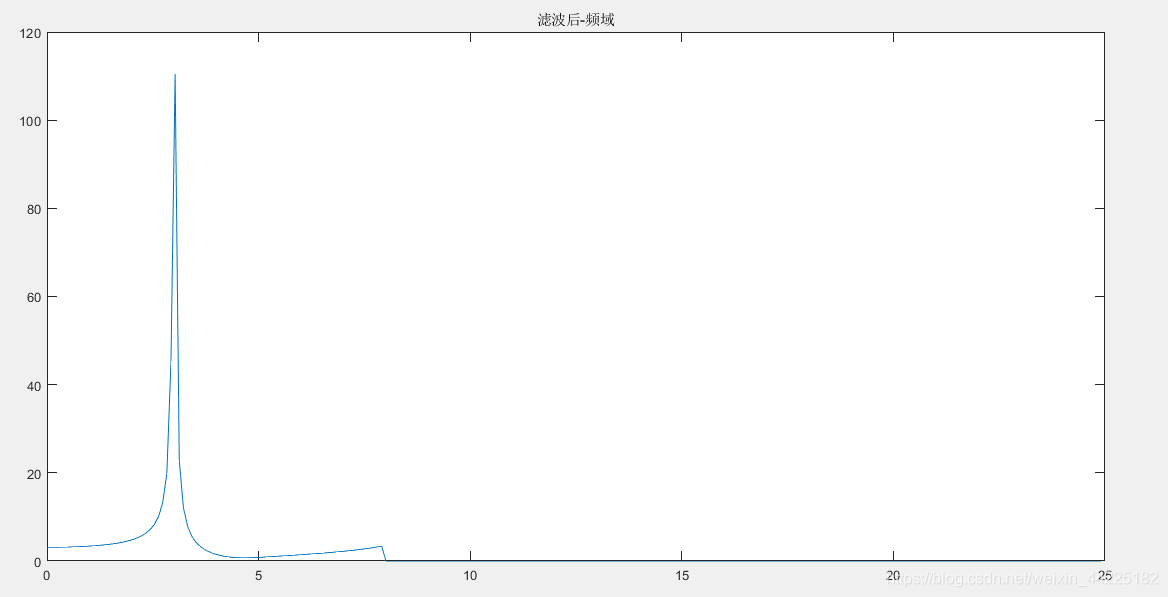
文章来源: haihong.blog.csdn.net，作者：海轰Pro，版权归原作者所有，如需转载，请联系作者。

原文链接：haihong.blog.csdn.net/article/details/102488649