Mathematics for Machine Learning--学习笔记:Linear Algebra【草稿 未完成】
Linear Algebra 线性代数
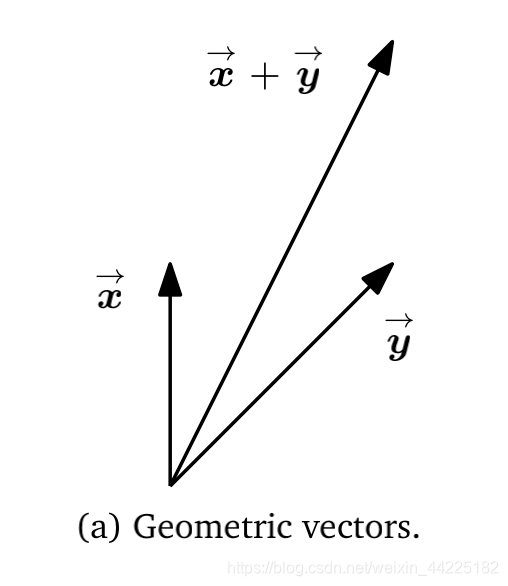
在形式化直观概念时,常用的方法是构造一组对象(符号)和一组规则来操纵这些对象。 这被称为代数。 线性代数是研究向量和某些代数规则来操纵向量。 我们中的许多人从学校知道的向量被称为“几何向量”,通常用字母就加上上方的一个小箭头表示,例如 x ⃗ \vec x x和 y ⃗ \vec y y。 在这本书中,我们讨论了向量的更一般的概念,并使用一个粗体字母来表示它们,例如:x和y。
一般来说,向量是特殊的对象:可以加在一起或乘以标量来产生另一个同类对象。 从抽象的数学观点来看,任何满足这两个性质的对象可以看作是一个向量。
以下是此类向量对象的一些示例:
-
几何矢量。 这个向量的例子可能是高中数学和物理所熟悉的。 几何向量是有向段,可以绘制(至少在二维空间)。 两个几何向量 x ⃗ \vec x x 、 y ⃗ \vec y y可以相加,使得 x ⃗ \vec x x+ y ⃗ \vec y y = z ⃗ \vec z z是另一个几何向量。 此外,乘以标量λ :λ x ⃗ \vec x x,λ ∈ \in ∈R,也是一个几何向量。 事实上它是由λ缩放的原始向量。 因此,几何向量是前面介绍的向量概念的实例。 将向量解释为几何向量可以使我们能够使用我们的直觉去感受数学运算的方向和大小。

-
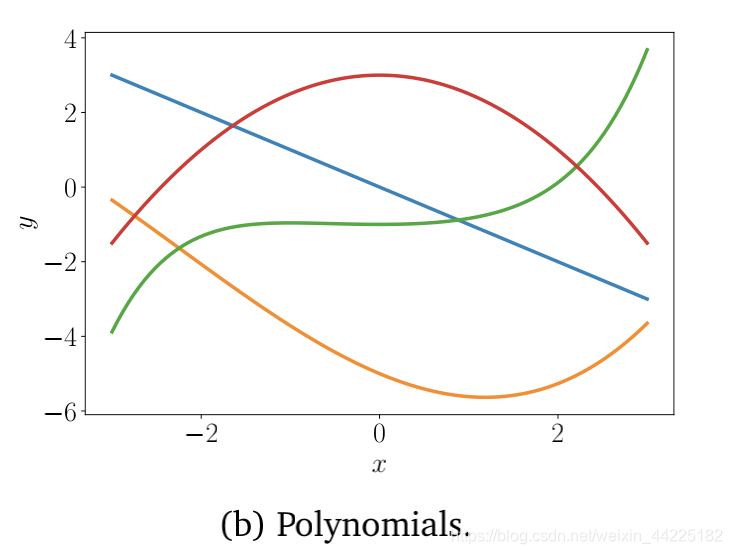
多项式也是向量;两个多项式可以相加,得到的结果也是一个多项式。它们可以乘以标量λ∈R,结果也是多项式。 因此,多项式是向量的(相当不寻常的)实例。 注意多项式与几何矢量有很大的不同。 几何向量是具体的“图”,多项式是抽象的概念。 然而,它们都是先前描述的意义上的向量。

-
音频信号是矢量。 音频信号表示为一系列数字。 我们可以把音频信号加在一起,它们的和是一个新的音频信号。 如果我们缩放一个音频信号,我们也得到一个 音频信号。 因此,音频信号也是一种矢量。
-
元素 R n R^n Rn(n个实数的元组)是向量。 与多项式相比, R n R^n Rn更抽象,它是我们在本书中关注的概念。例如a= [ 1 2 3 ] ∈
⎡⎣⎢123⎤⎦⎥\in ⎣⎡123⎦⎤∈ R 3 R^3 R3是一个三重数的例子。 添加两个向量a,b ∈ \in ∈ R 3 \R^3 R3分量将导致另一个向量:a+b=c ∈ \in ∈ R 3 R^3 R3。 此外,将a ∈ \in ∈ R 3 R^3 R3乘以λ ∈ \in ∈R将导致缩放向量λa ∈ \in ∈ R n R^n Rn 。 考虑向量作为 R n R^n Rn的元素,注意检查有一个额外的好处,即数组操作在计算机上实现时是否实际执行向量操作。 它松散地相关 计算机上的实数数组。 许多编程语言支持数组操作,这允许方便地实现涉及向量操作的算法。
线性代数侧重于这些向量概念之间的相似性。 我们可以把它们加在一起、用标量乘以它们。 我们将主要讨论关注 R n R^n Rn中的向量,因为线性代数中的大多数算法都是在 R n R^n Rn中制定的。
数学的一个主要思想是“封闭”的思想”。 这就是问题:我提出的操作可以产生的所有事物的集合是什么? 在向量的情况下:从一组小的向量开始,并将它们添加到彼此中并缩放它们,可以产生什么样的向量集? 这导致向量空间。 向量空间的概念及其恰当性是机器学习的基础。
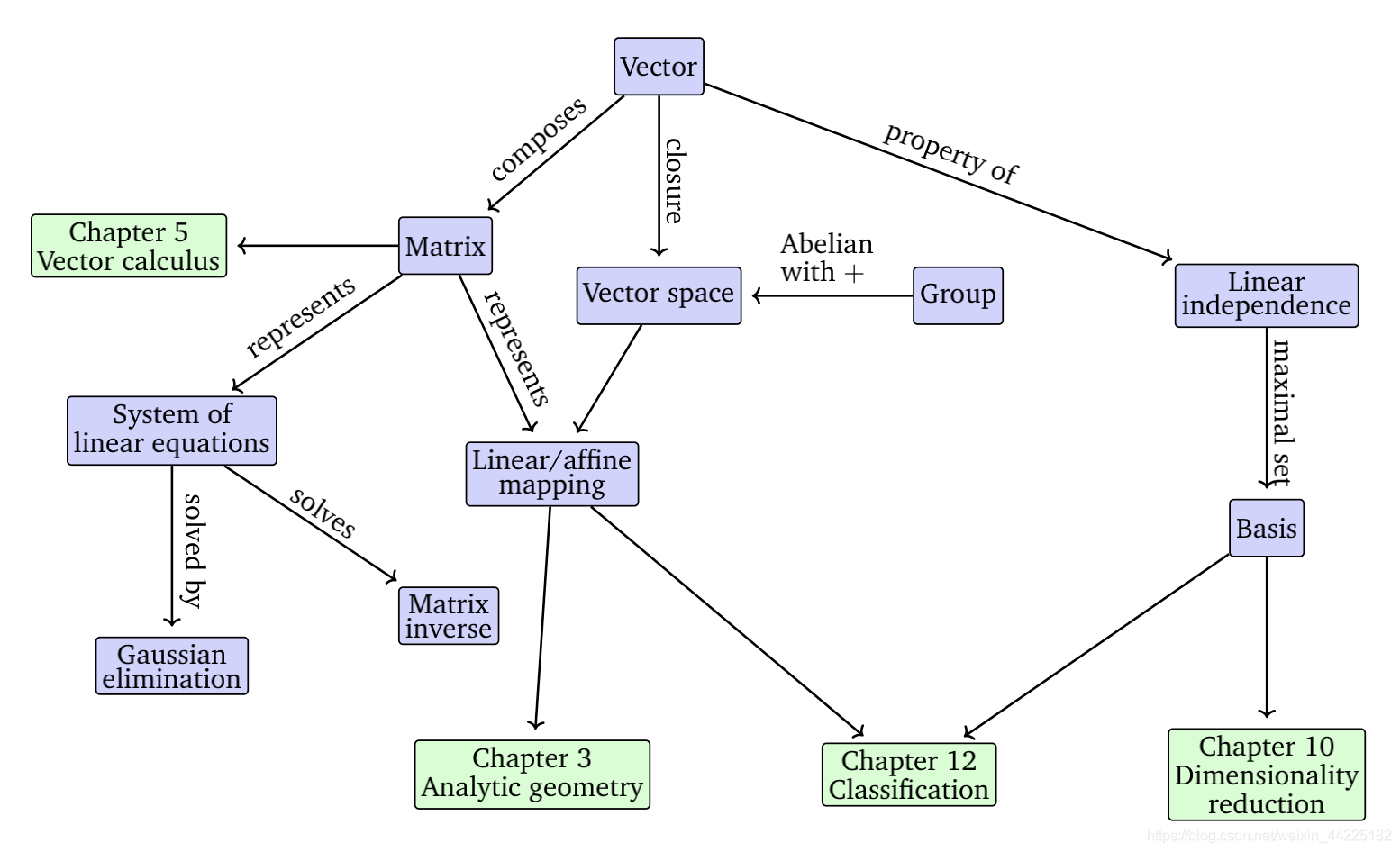
2.1 Systems of Linear Equations 线性方程组
线性方程组是线性代数的核心部分。 许多问题可以表述为线性方程组,线性代数给出了求解它们的工具。
例:一家公司生产 N 1 N_1 N1… N n N_n Nn的产品,每种产品需要 R 1 R_1 R1… R m R_m Rm的资源。 要生产一个单位的产品 N j N_j Nj,需要 a i j a_{ij} aij个单位的资源 R i R_i Ri,其中i=1…m和j=1…n
目标是找到一个最优的生产计划。如果总共 b i b_i bi个资源单位Ri都被利用完全,(理想情况下)没有浪费。那么应该生产 x j x_j xj个产品 N j N_j Nj
如果我们生产 x 1 x_1 x1… x n x_n xn个单位的相应产品,我们需要资源 R i R_i Ri的数量是:
a i 1 x 1 + . . . + a i n x n a_{i1}x_1+...+a_{in}x_n ai1x1+...+ainxn
因此,最优生产计划 ( x 1 x_1 x1… x n x_n xn) ∈ R n R^n Rn必须满足以下方程组
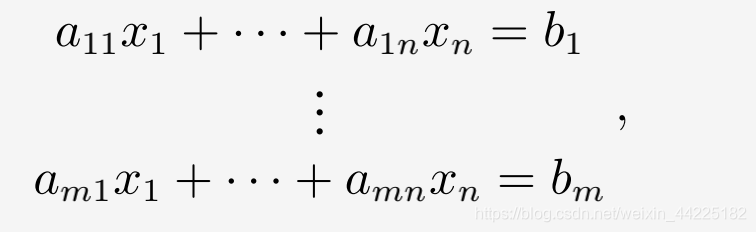
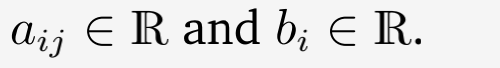
这就是个线性方程组一般形式了。也就是找最优解的数学模型。对应的 x 1 x_1 x1… x n x_n xn就是一组解。
例:下面这个线性方程组是没有解的:(1)+(2)=2 x 1 x_1 x1+3 x 3 x_3 x3=5,无解
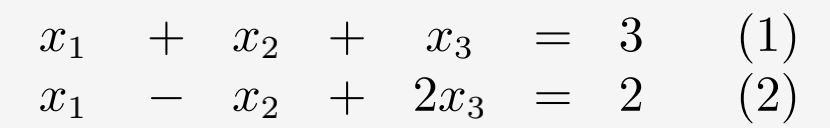
再看一个线性方程组
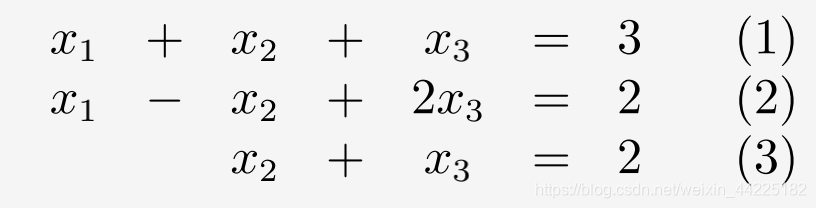
可以解出: x 1 x_1 x1=1, x 2 x_2 x2=1, x 3 x_3 x3=1
再看一个线性方程组
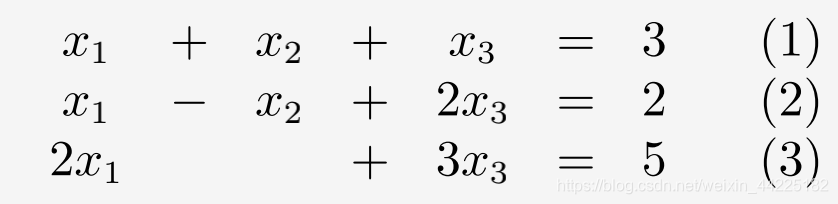
因为(1)+(2)=(3),所以(3)式是多余的。
(1)+(2)得到:2 x 1 x_1 x1+3 x 3 x_3 x3=5
(1)-(2)得到:2 x 2 x_2 x2- x 3 x_3 x3=1
定义 x 3 x_3 x3=a ∈ \in ∈ R ,作为一个自由变量,得到解
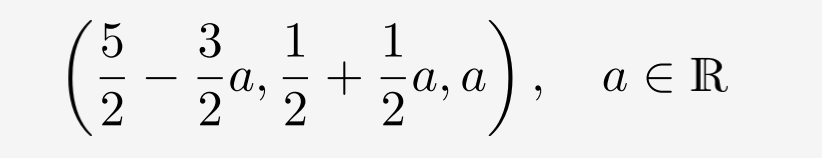
有无数个解
一般情况下,对于一个实值线性方程组,我们要么得到无解,要么是一个解,要么得到无穷多个解。
在一个只含两个变量 x 1 x_1 x1、 x 2 x_2 x2的线性方程组中,每一个线性方程代表xy坐标系中的一条直线。由于线性方程组的解必须同时满足所有方程,所以解集是这些直线的交点集合。这个交点集可以是一条线(如果线性方程描述同一条线)、一个点或空(当线平行时)。
例如:
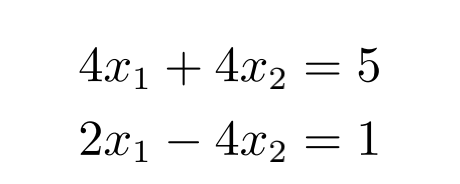
二维表示为:
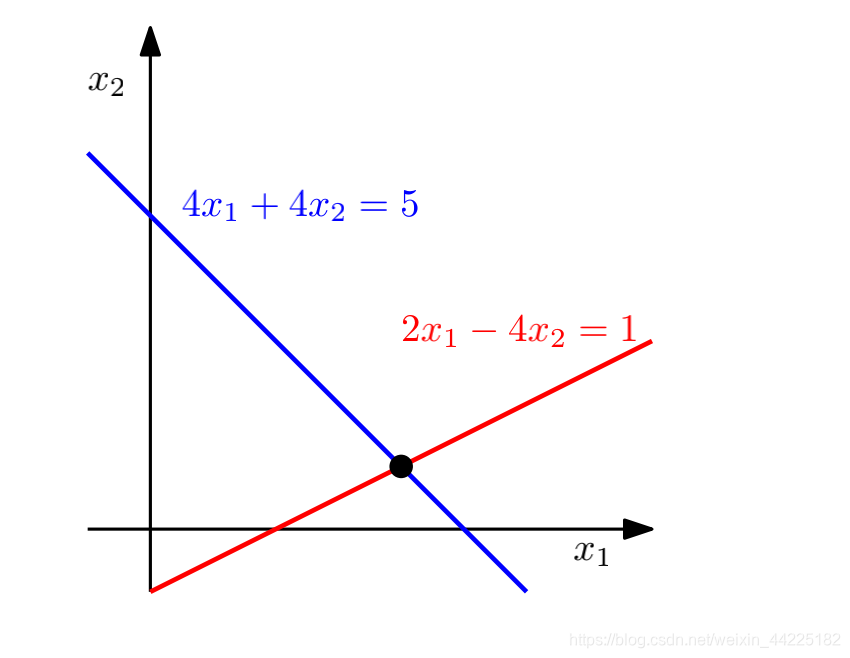
同样,对于三个变量,每个线性方程在三维空间中确定一个平面。 当我们相交这些平面,即同时满足所有线性方程时,我们可以得到 解集是平面、线、点或空(当平面没有公共交点时)。
对于求解线性方程组的系统方法,我们将引入一个有用的紧凑表示法。 我们将系数 a i j a_{ij} aij收集到向量中,并将向量收集到矩阵中。
换句话说,我们将
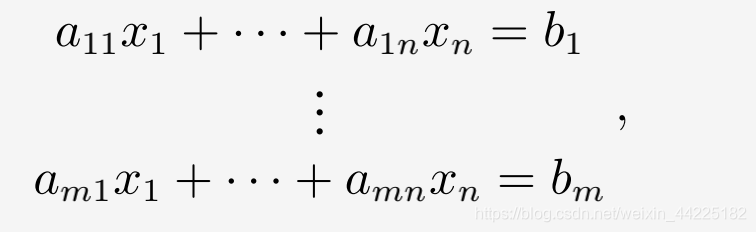
写成以下形式:

等价于:
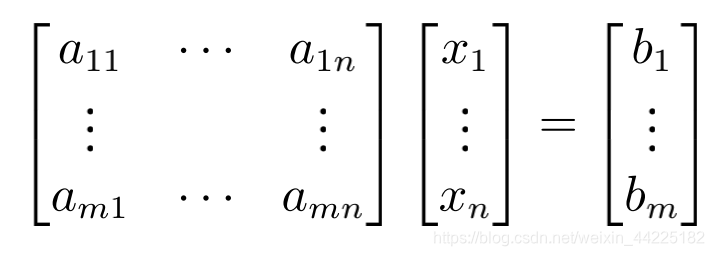
在下面,我们将仔细研究这些矩阵和去精细计算规则。
2.2 Matrices 矩阵
矩阵在线性代数中起着中心作用。 它们可以用来紧凑地表示线性方程组,但它们也表示线性函数(线性映射),我们将在后面看到 第2.7节。
在我们讨论这些有趣的主题之前,让我们首先定义矩阵是什么,以及我们可以对矩阵进行什么样的操作。 我们将在第4章中看到矩阵的更多性质。
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:

这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
2.2.1 Matrix Addition and Multiplication 矩阵加法和乘法
两个矩阵A∈Rm×n,B∈Rm和n定义为元素和,
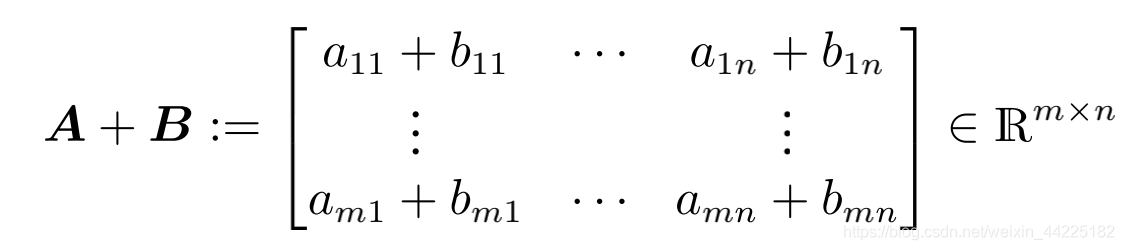
对于矩阵A∈RM×n,B∈Rn,k,注意乘积矩阵的元素CIJ的大小。 =AB∈Rm×k计算为
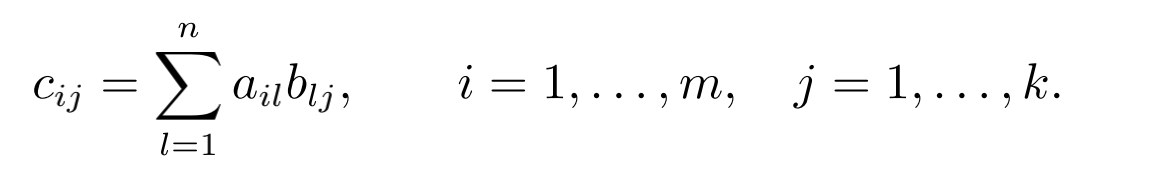
这意味着,为了计算元素CIJ,我们将ith的元素相乘,在A中有n列,在B中有n行,这样我们就可以计算l=1,…,n。通常,t之间的点积 WO向量a,b用>b或ha,bi表示。 用B的JTH列表示A行,并对它们进行总结。在第3.2节的后面,我们将把它称为相应行和列的点积。在需要显式表示正在执行乘法的情况下,我们使用表示法A·B表示乘法(显式显示“·”)。
矩阵只能在它们的“相邻”维度匹配的情况下乘以。 例如,n×k矩阵A可以与k×mm矩阵B相乘,但只能从左侧:
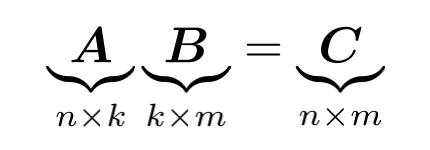
如果m=n,则不定义产品BA,因为相邻尺寸不匹配。
矩阵乘法不被定义为对矩阵元素的逐元运算,CIJ=AIJ Bij(即使A,B的大小被适当选择)。这种按元素计算的乘法经常出现在编程语言中,当我们彼此相乘(多维)数组时,被称为Hadamard积。
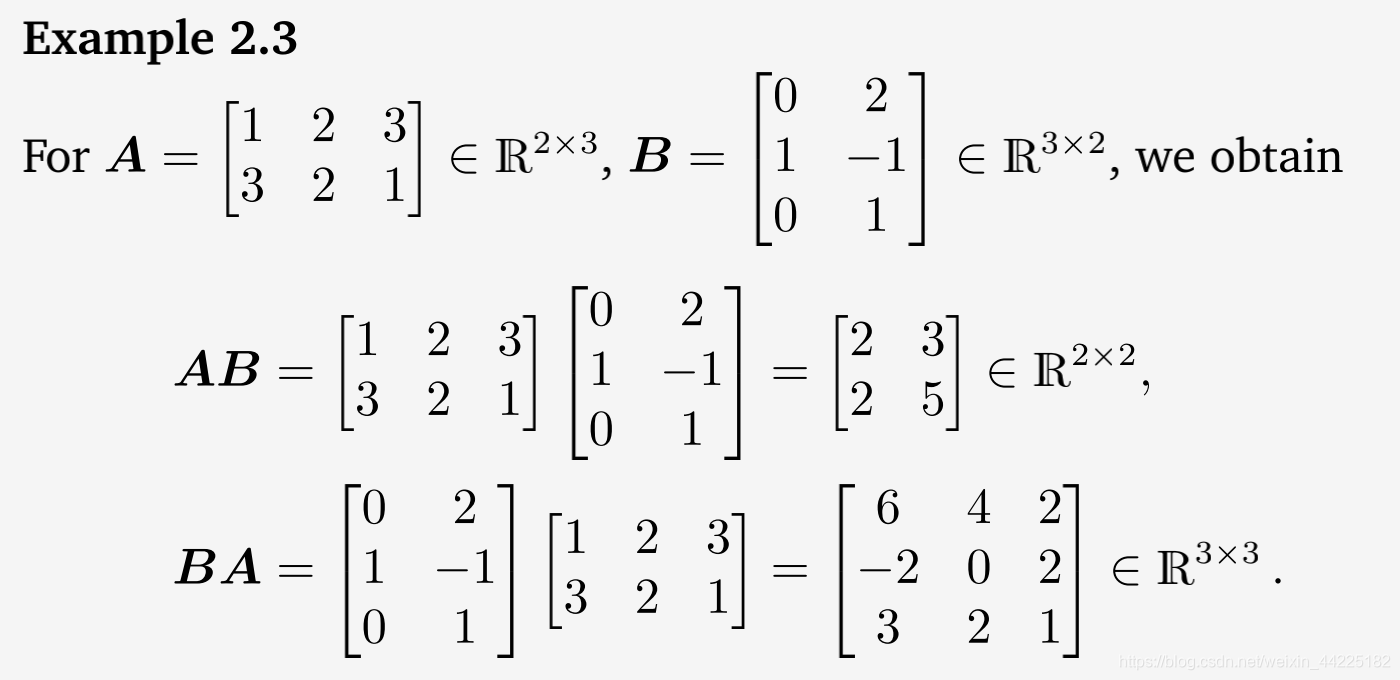
从这个例子中,我们已经可以看出矩阵乘法不是交换的。,AB=BA;请参见图2.5。
Identity Matrix 单位矩阵

现在我们定义了矩阵乘法、矩阵加法和恒等矩阵,让我们看看矩阵的一些性质:
Associativity 结合律
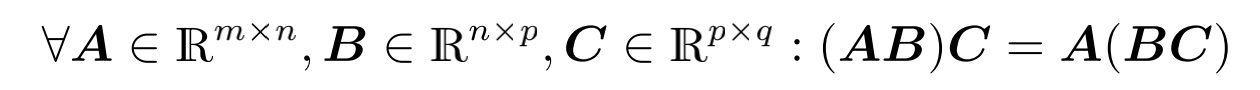
Distributivity 分配律
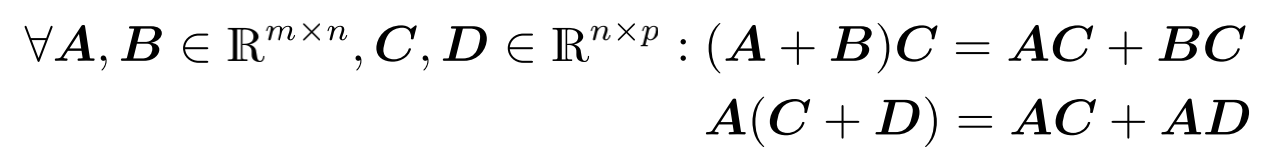
与恒等矩阵相乘
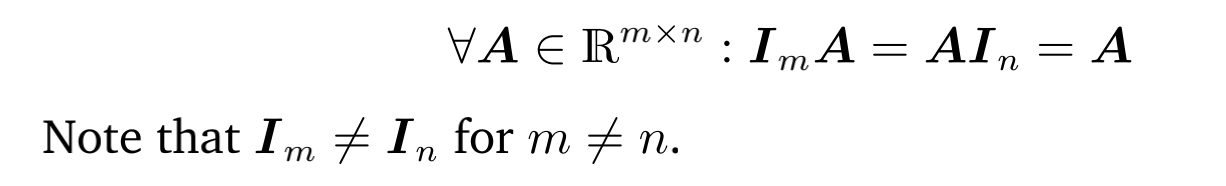
2.2.2 Inverse and Transpose 逆和转置
逆的定义:考虑一个方阵A∈Rn×n个方阵。 让矩阵拥有相同数量的列和行。 乙∈Rn×具有=BA中AB的性质。 称B为A的逆,表示b Y A1。
如果这个正则逆确实存在,则A称为正则/不可逆/不可逆,否则称为可逆的非奇异奇异/不可逆。当矩阵逆存在时,它是唯一的。在第2.3节中,我们将讨论一种通过求解线性方程组来计算矩阵逆的一般方法。
转置的定义:对于A∈Rm×n,矩阵B∈Rn×m与bij=aji称为A的转置。 我们写B=A>
一般地,A>可以通过将A的列写为A的行来获得。。 以下是逆和转置的重要性质:
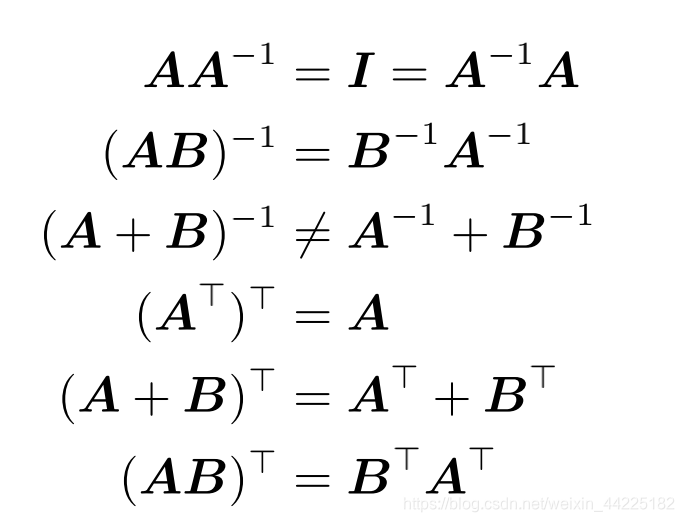
Symmetric Matrix 对称矩阵
如果对称矩阵为=,>,则矩阵是对称的。
注意,只有(n,n)矩阵可以是对称的。 通常,我们称(n,n)矩阵也是平方矩阵,因为它们具有相同的行和列的num-平方矩阵。 此外,如果A可逆的,那么A>也是,(A1)>=(A>)1:A−>。
对称矩阵的总和和乘积
对称矩阵A,B∈Rn×n的和总是对称的。 然而,虽然它们的乘积总是被定义的,但它通常不是对称的:
2.2.3 Multiplication by a Scalar 标量乘法
让我们看看当矩阵乘以标量λ时会发生什么∈R。让A∈Rm×n和λ∈R。然后λA K,Kij=Aij。
实际上,λ缩放A的每个元素。
交换律
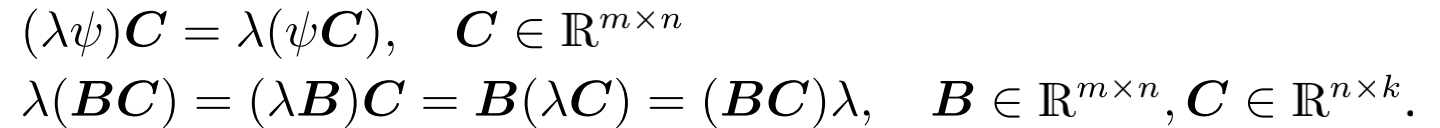
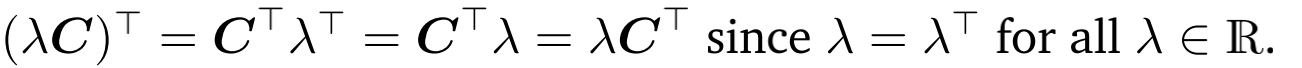
分配律
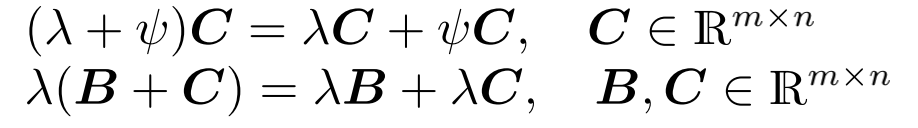
2.2.4 Compact Representations of Systems of Linear Equations 线性方程组的紧凑表示
如果考虑线性方程组

利用矩阵乘法的规则,我们可以把这个方程系统写成更紧凑的形式
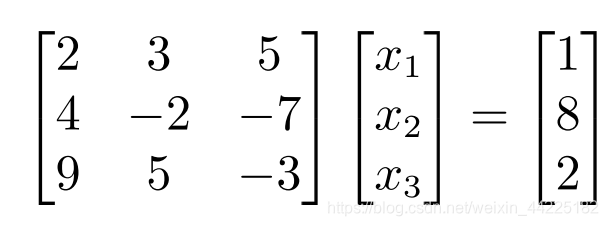
请注意,x1缩放第一列,x2缩放第二列,x3缩放第三列。
一般地,线性方程组可以用它们的矩阵形式紧凑地表示为Ax=b;参见(2.3),乘积Ax是A列的(线性)组合。 我们将讨论linea 第2.5节中更详细的r组合。
2.3 Solving Systems of Linear Equations 线性方程组的求解
我们介绍了方程系统的一般形式
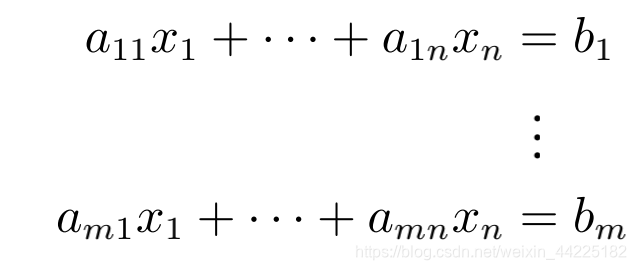
∈和∈是已知常数,∈是未知数,=1,…,=1,…到目前为止,我们看到矩阵可以作为一种紧凑的方法来构造线性等系统 这样我们就可以写出Ax=b,见(2.10)。此外,我们还定义了基本的矩阵运算,如矩阵的加法和乘法。 在下面,我们将重点解决线性方程组,并提供一个算法的查找 矩阵的逆。
2.3.1 Particular and General Solution 特殊和一般解决方案
在讨论如何一般地解线性方程组之前,让我们看看一个例子。 考虑方程组
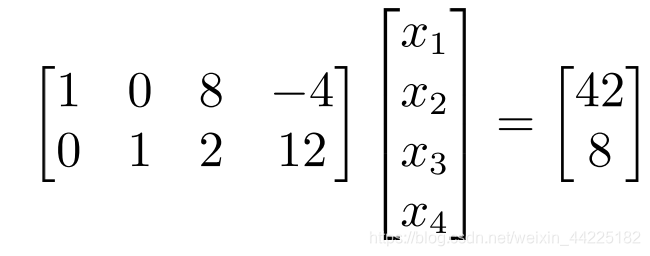
系统有两个方程和四个未知数。因此,一般来说,我们会期望无限多的解。这个方程组是一个特别容易的形式,其中前两列由1P和0组成.记住,我们想找到标量=1,…,例如,我们将其定义为矩阵的柱和(2.38)的右手边。通过将第一列的42倍和第二列的8倍,可以立即找到(2.38)中问题的解决方案
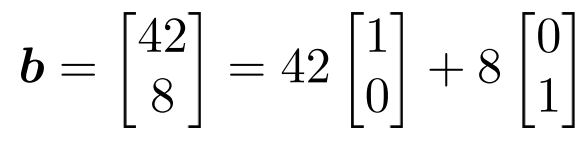
因此,一个解决方案是[42,8,0,0]> 该解称为特定的解解或特殊解。然而,这不是线性方程组的唯一解。为了捕获所有其他解决方案,我们需要创造性地使用矩阵的列以非平凡的方式生成0 在我们的特殊解决方案中添加0不会改变特殊解决方案。 为此,我们使用前两列表示第三列((这是非常简单的形式)
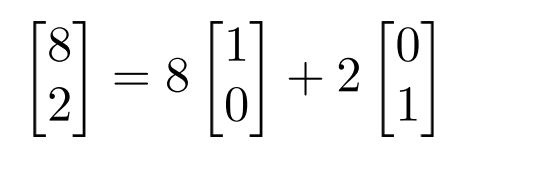
前面例子中的线性方程组很容易求解,因为(2.38)中的矩阵具有这种特别方便的形式,使我们能够找到特定的和一般的s 通过检查进行洗脱。然而,一般方程系统不是这种简单的形式.幸运的是,有一种建设性的算法方法将任何线性方程组转化为这种特别简单的形式:高斯消除.高斯消去的关键是线性方程组的初等变换,它将方程组转化为简单形式。 然后,我们可以将这三个步骤应用于简单的for 我们刚才在(2.38)中的示例中讨论了这一点)
2.3.2 Elementary Transformations 初等变化
解线性方程组的关键是保持解集相同的初等变换,但将方程系统转化为更简单的形式
- 交换两个方程(表示方程组的矩阵中的行)
- 方程(行)与R{0}∈常数λ的乘法}
- 增加两方程(行)
对于∈R,我们寻求下列方程组的所有解:
文章来源: haihong.blog.csdn.net,作者:海轰Pro,版权归原作者所有,如需转载,请联系作者。
原文链接:haihong.blog.csdn.net/article/details/113181128
- 点赞
- 收藏
- 关注作者


评论(0)