深度学习笔记（四）：梯度下降法与局部最优解

在深度学习过程中，避免不了使用梯度下降算法。但是对于“非凸问题”，训练得到的结果往往可能陷入局部极小值，而非全局最优解。那么这里就以Himmelblau 函数为例，探究待优化参数的初始值对梯度下降方向的影响，从而得到不同的局部极小值。
首先介绍一下Himmelblau 函数：

下图 为 Himmelblau 函数的等高线，大致可以看出，它共有 4 个局部极小值点，并且局部极小值都是 0，所以这 4 个局部极小值也是全局最小值。我们可以通过解析的方法计算出局部极小值坐标，他们分别是(3,2), (−2 805,3 131), (−3 779,−3 283), (3 584,−1 848)。

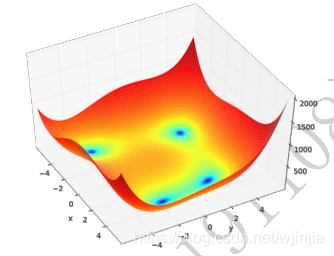
在已经知道极小值解的情况下，我们现在来用梯度下降算法来优化 Himmelblau 函数的数值极小值解。
程序清单：

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def himmelblau(x): return (x[0]**2 + x[1] - 11)**2 + (x[0] + x[1]**2-7)**2
x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
X, Y = np.meshgrid(x, y)  # 生成x-y平面网格点，方便可视化
print('X,Y maps:', X.shape, Y.shape)
Z = himmelblau([X, Y])  # 调用函数，计算函数值
fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)  # 绘制3D图形
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_ylabel('z')
plt.show()

x = tf.constant([4., 0.])  # 初始化参数（下面的实验只需要改这一行的参数）

for step in range(200): with tf.GradientTape() as tape:  # 梯度跟踪 tape.watch([x])  # 加入梯度跟踪列表 y = himmelblau(x)  # 向前传播 grads = tape.gradient(y, [x])[0]  # 梯度计算 x -= 0.01*grads  # 梯度下降 if step % 20 == 19: print('step{}: x,y={}; H(x,y)={}'.format(step, x.numpy(), y.numpy()))


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
 

在上面代码中，我们只需要改初始化参数，来看看对最终结果的影响
（1）第一次，选取初始点为（4，0），经过200轮迭代训练后，得到的极小值处为：（3.584，-1.848），极小值接近0。训练结果如下：

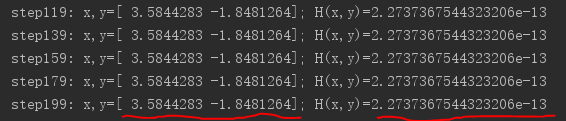
（2）第二次，选取初始点（1，0），训练结果如下：

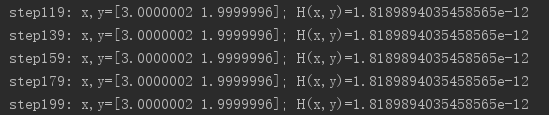
（3）第三次，选取初始点（-4，0），训练结果如下：

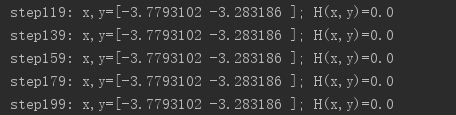
（4）第四次，选取初始点（-2，2），训练结果如下：

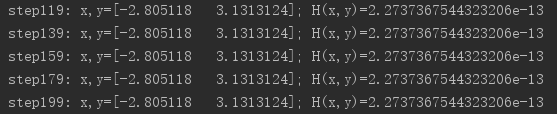
统计上面的四次实验得到的数值结果，与我们通过笔算得到的解析解进行比较，如下表：

可得出如下结论：
（1）通过梯度下降法训练得到的数值最优解（极小值），几乎等于解析解。
（2）当对待优化参数x初始化为不同的值时，最后对应的最优解（极小值）处也不相同。
这表明：通过梯度下降算法迭代得到的最优解（局部极小值）位置与待优化参数的初始值密切相关

文章来源: ai-wx.blog.csdn.net，作者：AI 菌，版权归原作者所有，如需转载，请联系作者。

原文链接：ai-wx.blog.csdn.net/article/details/104763111