【算法与数据结构 05】后进先出的栈——顺序栈、链栈知多少?
1.栈的简介
简单来说,栈是一种特殊的线性表。
线性表对数据的顺序非常敏感,而且它对数据的增删操作非常灵活。在有序排列的数据中,可以灵活的执行增删操作,就好像是为排好队的数据增加了插队的入口。这既是灵活性也是缺陷,原因在于它的灵活性在某种程度上破坏了数据的原始顺序。在某些需要严格遵守数据处理顺序的场景下,我们就需要对线性表予以限制了。而栈就是一种被限制的线性表。
既然线性表那么灵活,那为啥还需要栈呢?
其实,单纯从功能上讲,线性表(数组或链表)可以替代栈。然而问题是,数组或者链表的操作过于灵活,这意味着,它们过多暴露了可操作的接口。这些没有意义的接口过多,当数据量很大的时候就会出现一些隐藏的风险。所以虽然栈限定降低了操作的灵活性,但也使得增删数据时,安全性和时效性更高。
那么具体是怎么限制的呢?
栈的数据结点被限制为后进先出,这意味着栈的数据新增操作只能在末端进行,不允许在栈的中间某个结点后新增数据。同时,栈的数据删除操作也只能在末端进行,不允许在栈的中间某个结点后删除数据。
因此,可以说栈是一种后进先出的线性表。
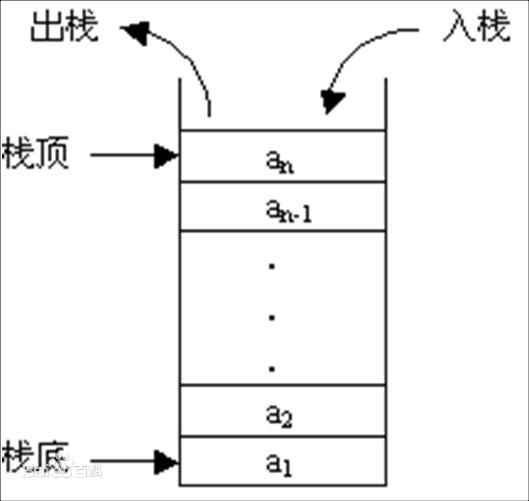
2. 栈的基本操作
栈有两种基本的操作:压栈与出栈。
如果需要给栈新增数据,就是压栈,也称作push。
如果需要删除栈顶的数据,就是出栈,也称作pop。
前面我们学习了线性表,知道线性表有顺序存储结构的数组,也有采用链式存储结构的链表。同理,根据存储结构的不同,栈也被分为了顺序栈和链栈。
下面就来分别谈一下顺序栈和链栈的增删查操作。
(1)顺序栈
栈的顺序存储可以借助数组来实现。一般来说,会把数组的首元素存在栈底,最后一个元素放在栈顶。然后定义一个 top 指针来指示栈顶元素在数组中的位置。 假设栈中只有一个数据元素,则 top = 0。一般以 top 是否为 -1 来判定是否为空栈。 当定义了栈的最大容量为 StackSize 时,则栈顶 top 必须小于 StackSize。
- 新增操作。就需要将新插入元素放在栈顶,并将栈顶指针增加 1。
- 删除操作。即出栈操作,只需要 top - 1 就可以了。
- 查找操作。栈没有额外的改变,跟线性表一样,它也需要遍历整个栈来完成基于某些条件的数值查找。
(2)链栈
关于链栈,就是用链表的方式对栈的表示。通常,可以把栈顶放在单链表的头部。由于链栈的后进先出,原来的头指针就显得毫无作用了。因此,对于链栈来说,是不需要头指针的。相反,它需要增加指向栈顶的 top 指针,这是压栈和出栈操作的重要支持。
- 新增操作。即压栈操作,与链表最后插入的新数据基本相同。需要额外处理的,就是栈的 top 指针。插入新的数据,则需要让新的结点指向原栈顶,即 top 指针指向的对象,再让 top 指针指向新的结点。
- 删除操作。只能在栈顶进行操作,因此,将栈顶的 top 指针指向栈顶元素的 next 指针即可完成删除。
- 查找操作。相对链表而言,链栈没有额外的改变,它也需要遍历整个栈来完成基于某些条件的数值查找。
对于链式栈来说,新增删除数据元素没有任何循环操作,其时间复杂度均为 O(1)。
通过分析你会发现,不管是顺序栈还是链栈,数据的新增、删除、查找与线性表的操作原理极为相似,时间复杂度完全一样,都依赖当前位置的指针来进行数据对象的操作。区别仅仅在于新增和删除的对象,只能是栈顶的数据结点。
3. push和pop的使用
如下图所示,使用push和pop分别在栈顶位置增加和删除元素。
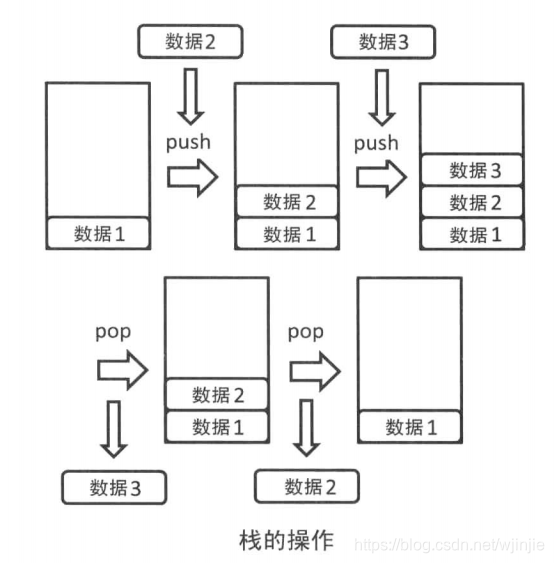
如下所示,先向栈中存入三个元素,再从栈中取出一个元素。
#include<iostream>
#include<stack>
using namespace std;
int main()
{
stack<int> s;
s.push(1);
s.push(2);
s.push(3);
cout<<"栈顶的数是:"<<s.top()<<endl;
s.pop();
cout<<"执行一次pop操作后,栈顶的数是:"<<s.top()<<endl;
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
运行结果:
栈顶的数是:3
执行一次pop操作后,栈顶的数是:2
- 1
- 2
4. 总结
- 栈具有后进先出的特性,只允许数据从栈顶进出。
- 栈对于数据的新增操作和删除操作的时间复杂度都是 O(1)。而在查找操作中,栈和线性表一样只能通过全局遍历的方式进行,也就是需要 O(n) 的时间复杂度。
- 当你面对的问题需要高频使用新增、删除操作,且新增和删除操作的数据执行顺序具备后来居上的相反关系时,栈就是个不错的选择。
文章来源: ai-wx.blog.csdn.net,作者:AI 菌,版权归原作者所有,如需转载,请联系作者。
原文链接:ai-wx.blog.csdn.net/article/details/107356912
- 点赞
- 收藏
- 关注作者


评论(0)