【算法与数据结构 10】哈希表——高效查找的利器

前言：

之前，我们先后学习了线性表、数组、字符串和树，它们普遍都存在这样的缺陷，那就是数据数值条件的查找，都需要对全部数据或者部分数据进行遍历。那么，有没有一种方法可以省去数据比较的过程，从而进一步提升数值条件查找的效率呢？

答案当然是：有！这一课时我们就来介绍这样一种高效率的查找神器：哈希表。

一、什么是哈希表

哈希表名字源于 Hash，也可以叫作散列表。哈希表是一种特殊的数据结构，它与数组、链表以及树等我们之前学过的数据结构相比，有很明显的区别。

1.1 哈希表的原理

哈希表是一种数据结构，它使用哈希函数组织数据，以支持快速插入和搜索。哈希表的核心思想就是使用哈希函数将键映射到存储桶。更确切地说：

• 当我们插入一个新的键时，哈希函数将决定该键应该分配到哪个桶中，并将该键存储在相应的桶中；
• 当我们想要搜索一个键时，哈希表将使用相同的哈希函数来查找对应的桶，并只在特定的桶中进行搜索。

下面举一个简单的例子，我们来理解下：

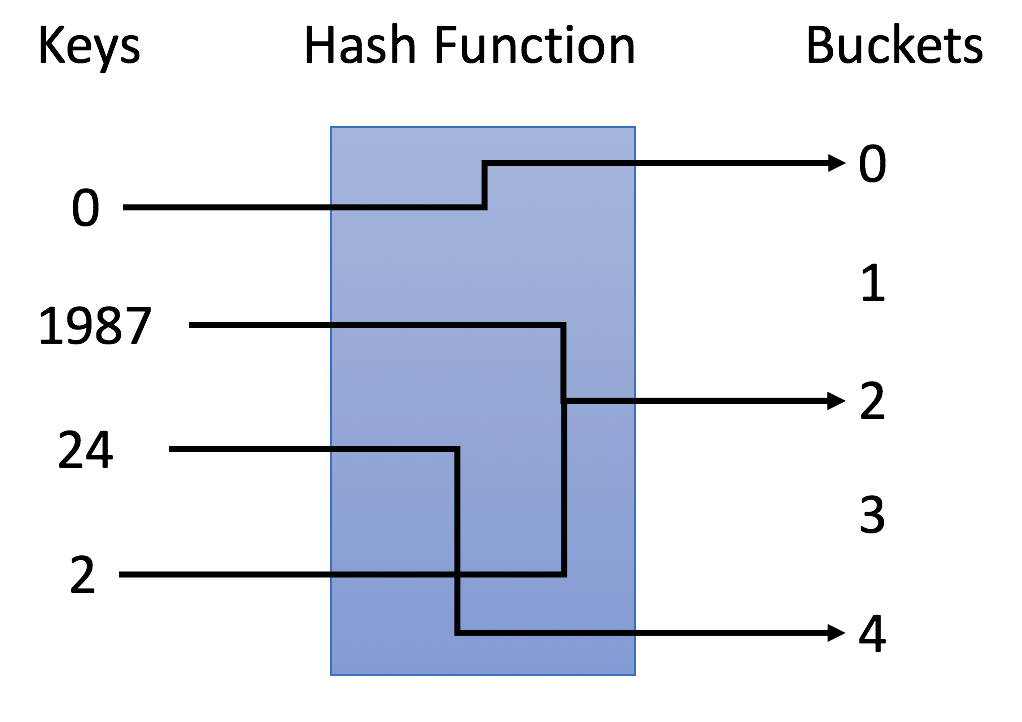
在示例中，我们使用 y = x ％ 5 作为哈希函数。让我们使用这个例子来完成插入和搜索策略：

• 插入：我们通过哈希函数解析键，将它们映射到相应的桶中。 例如，1987 分配给桶 2，而 24 分配给桶 4。
• 搜索：我们通过相同的哈希函数解析键，并仅在特定存储桶中搜索。 例如，如果我们搜索 23，将映射 23 到 3，并在桶 3 中搜索。我们发现 23 不在桶 3 中，这意味着 23 不在哈希表中。

1.2 设计哈希函数

哈希函数是哈希表中最重要的组件，该哈希表用于将键映射到特定的桶。在之前的示例中，我们使用 y = x % 5 作为散列函数，其中 x 是键值，y 是分配的桶的索引。

散列函数将取决于键值的范围和桶的数量。下面是一些哈希函数的示例：

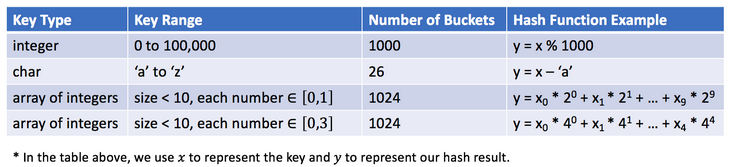
哈希函数的设计是一个开放的问题。其思想是尽可能将键分配到桶中，理想情况下，完美的哈希函数将是键和桶之间的一对一映射。然而，在大多数情况下，哈希函数并不完美，它需要在桶的数量和桶的容量之间进行权衡。

当然，我们也可以自定义一些哈希函数。一般的方法有：

• 直接定制法。哈希函数为关键字到地址的线性函数。如，H (key) = a * key + b。 这里，a 和 b 是设置好的常数。
• 数字分析法。假设关键字集合中的每个关键字 key 都是由 s 位数字组成（k1,k2,…,Ks），并从中提取分布均匀的若干位组成哈希地址。
• 平方取中法。如果关键字的每一位都有某些数字重复出现，并且频率很高，我们就可以先求关键字的平方值，通过平方扩大差异，然后取中间几位作为最终存储地址。
• 折叠法。如果关键字的位数很多，可以将关键字分割为几个等长的部分，取它们的叠加和的值（舍去进位）作为哈希地址。
• 除留余数法。预先设置一个数 p，然后对关键字进行取余运算。即地址为 key % p。

二、解决哈希冲突

理想情况下，如果我们的哈希函数是完美的一对一映射，我们将不需要处理冲突。不幸的是，在大多数情况下，冲突几乎是不可避免的。例如，在我们之前的哈希函数（y = x ％ 5）中，1987 和 2 都分配给了桶 2，这就是一个哈希冲突。

解决哈希冲突应该要思考以下几个问题：

• 如何组织在同一个桶中的值？
• 如果为同一个桶分配了太多的值，该怎么办？
• 如何在特定的桶中搜索目标值？

那么一旦发生冲突，我们该如何解决呢？

常用的方法有两种：开放定址法和链地址法。

2.1 开放定址法

即当一个关键字和另一个关键字发生冲突时，使用某种探测技术在哈希表中形成一个探测序列，然后沿着这个探测序列依次查找下去。当碰到一个空的单元时，则插入其中。

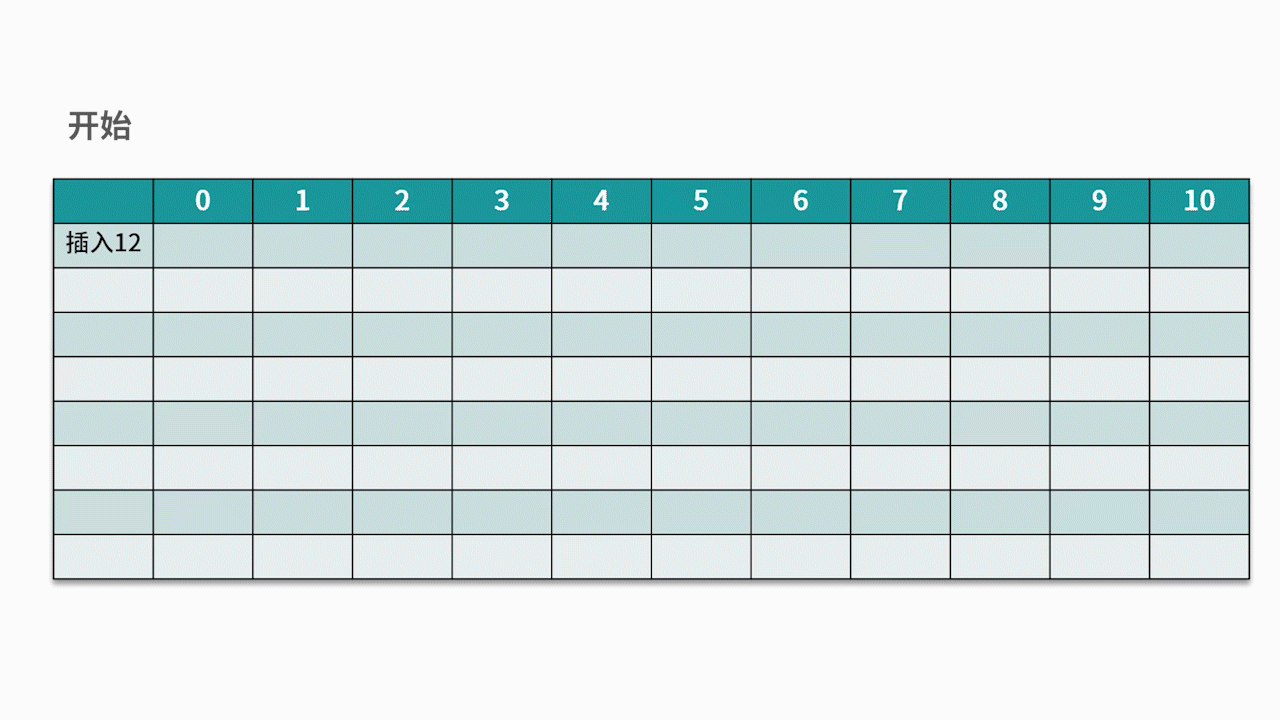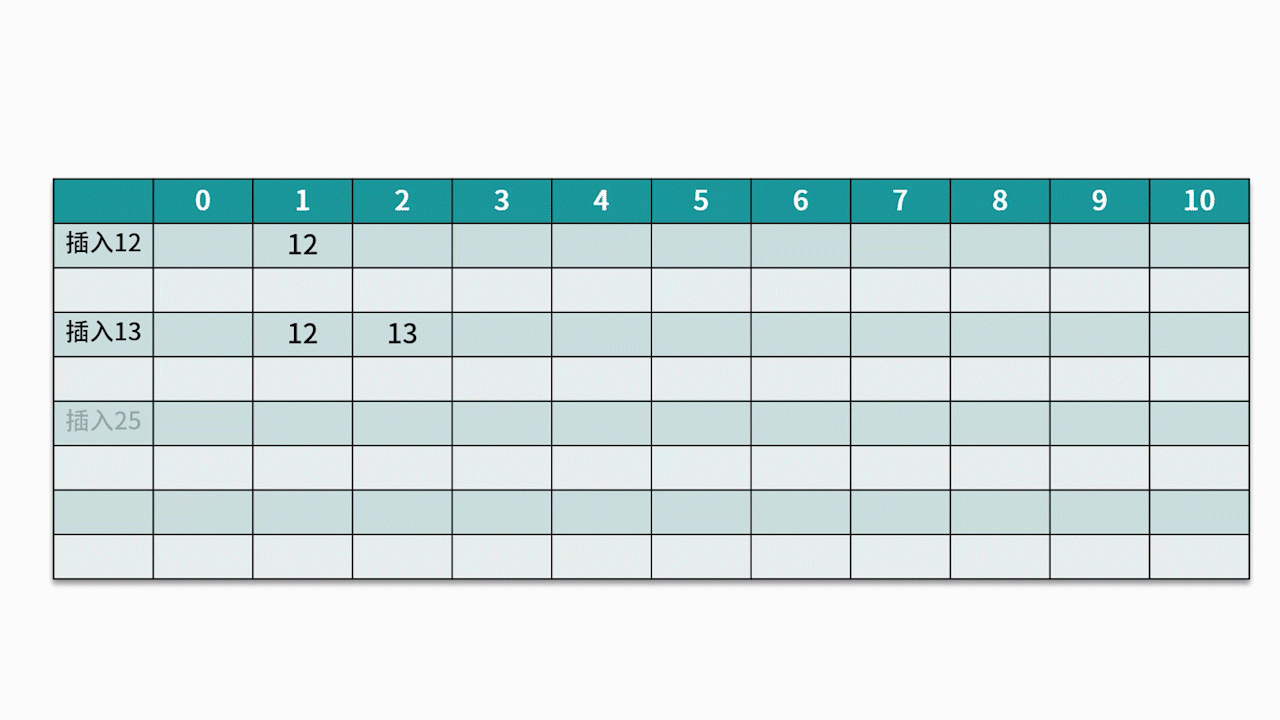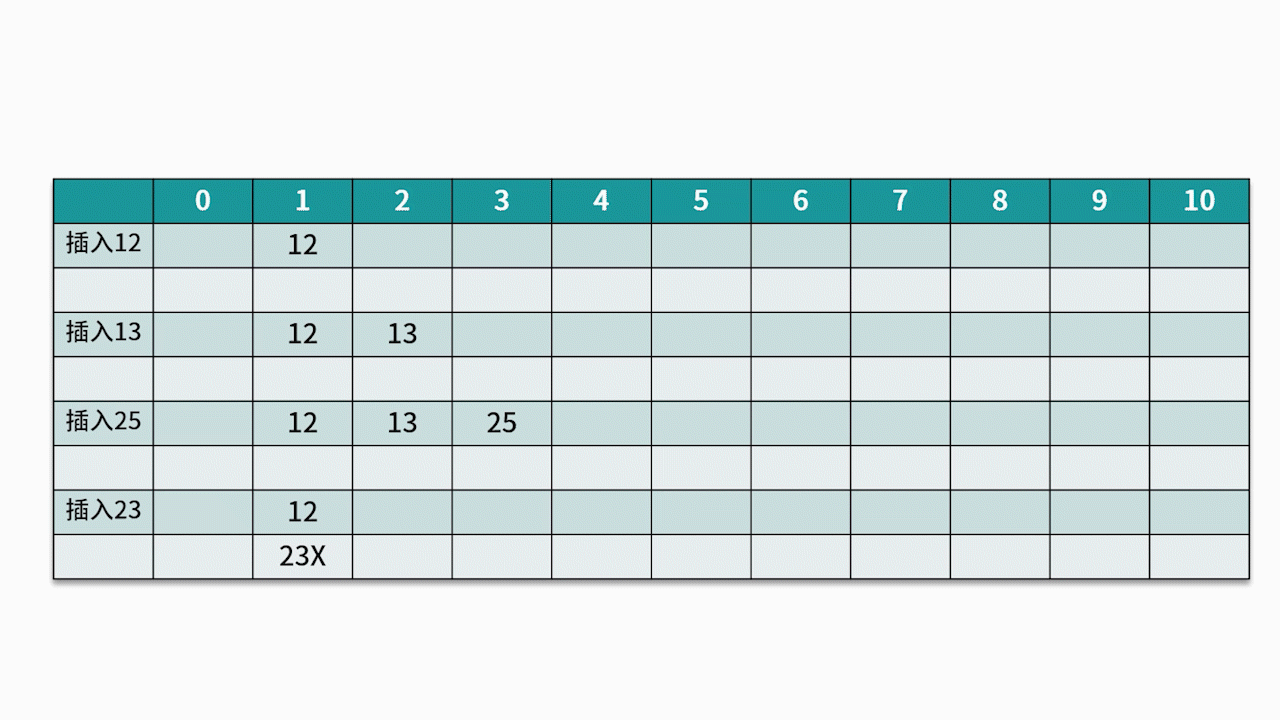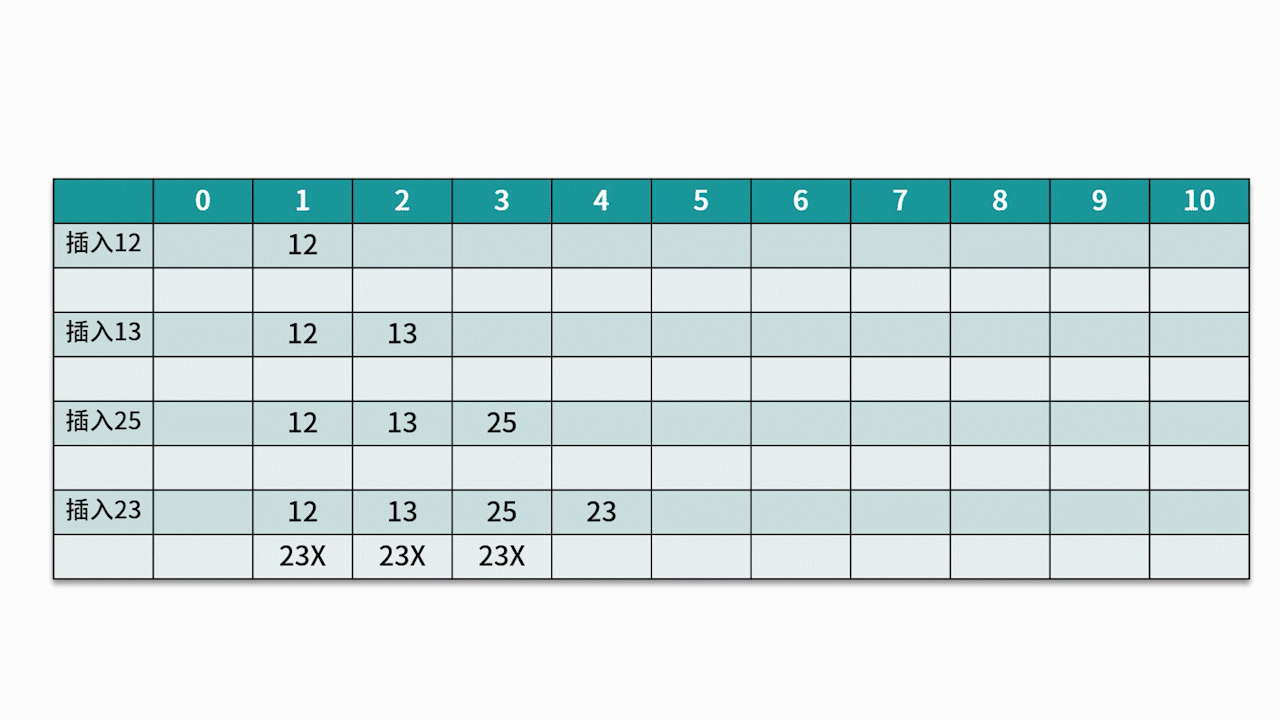
常用的探测方法是线性探测法。 比如有一组关键字 {12，13，25，23}，采用的哈希函数为 key % 11。当插入 12，13，25 时可以直接插入，地址分别为 1、2、3。而当插入 23 时，哈希地址为 23 % 11 = 1。

然而，地址 1 已经被占用，因此沿着地址 1 依次往下探测，直到探测到地址 4，发现为空，则将 23 插入其中。如下图所示：

2.2 链地址法

将哈希地址相同的记录存储在一张线性链表中。例如，有一组关键字 {12,13,25,23,38,84,6,91,34}，采用的哈希函数为 key % 11。如下图所示：

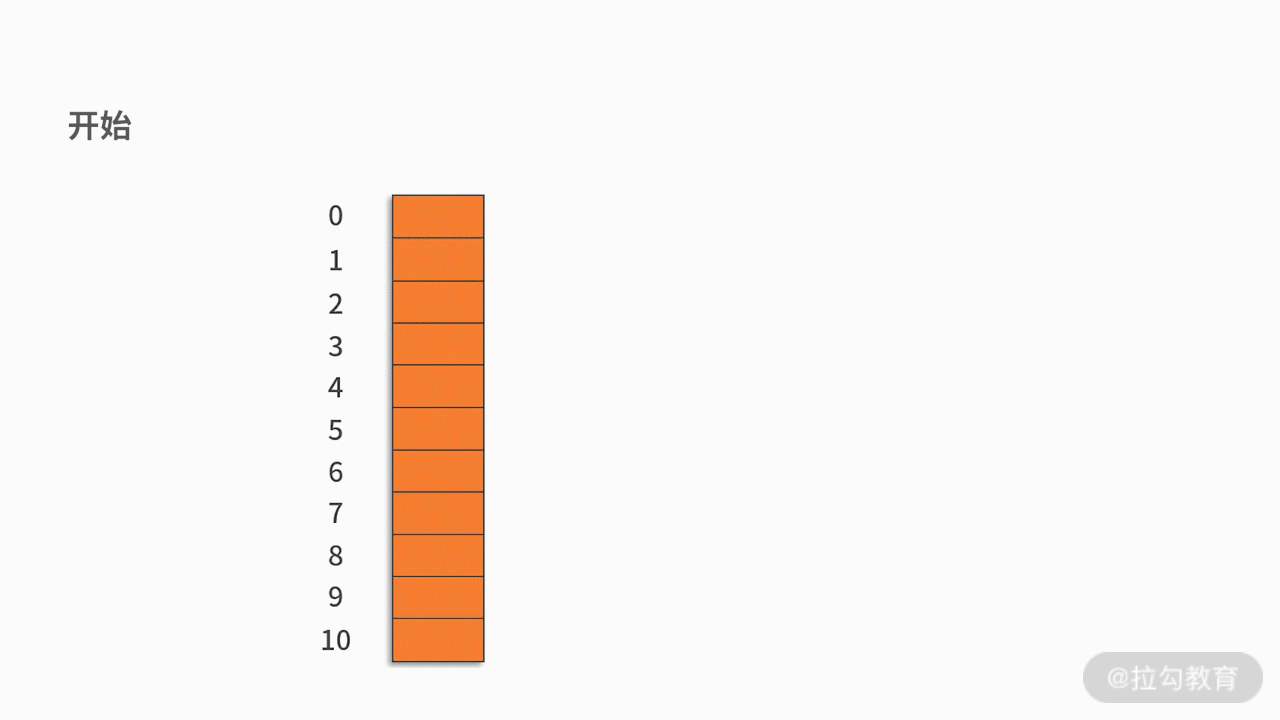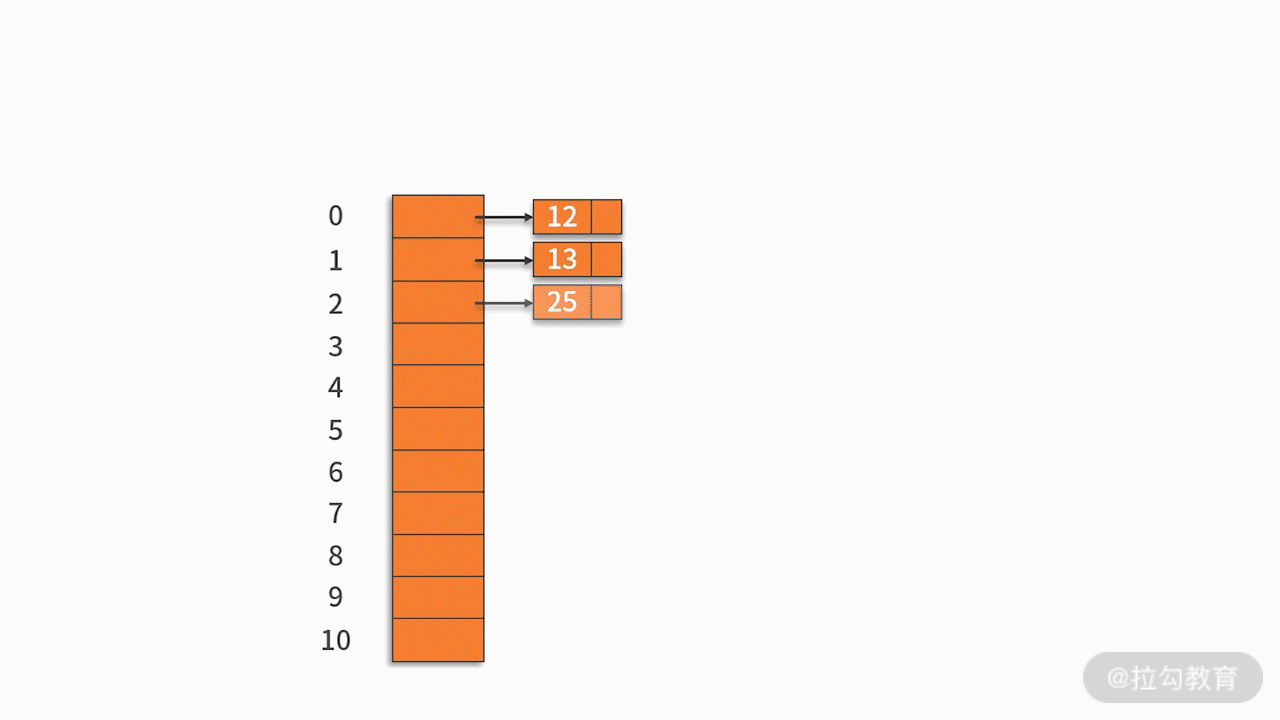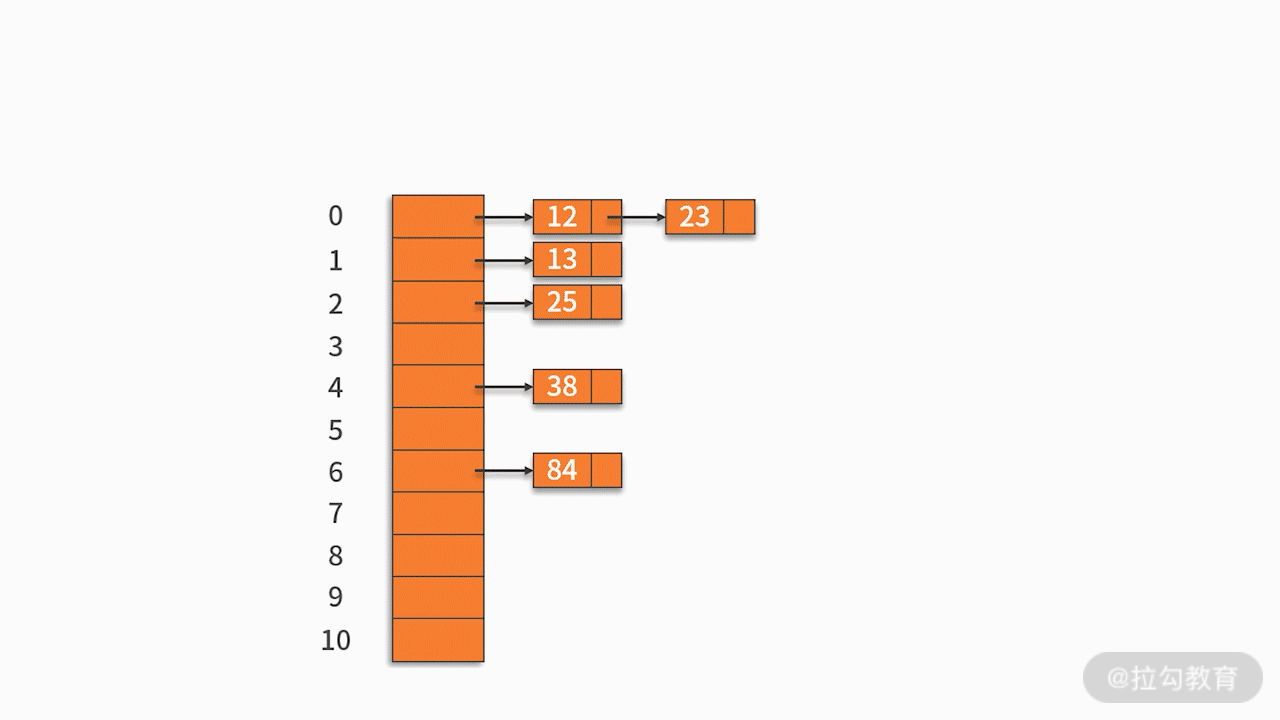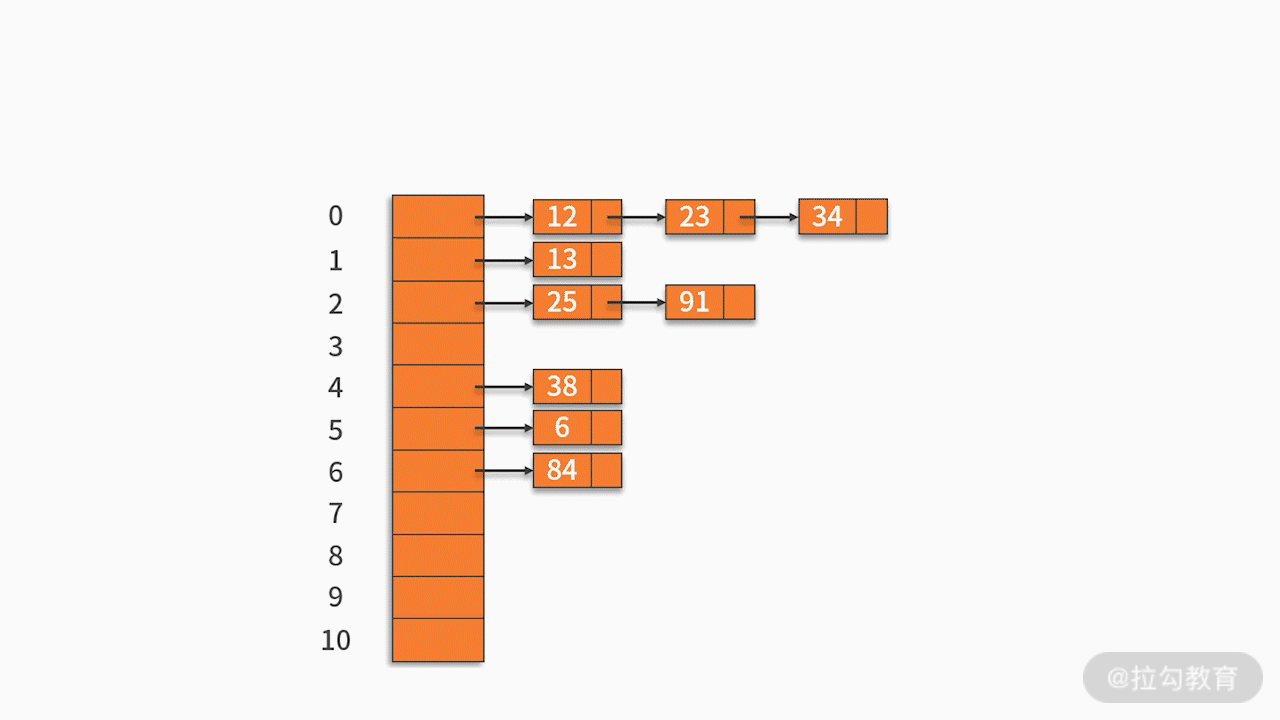
三、哈希表的应用

3.1 哈希表的基本操作

在很多高级语言中，哈希函数、哈希冲突都已经在底层完成了黑盒化处理，是不需要开发者自己设计的。也就是说，哈希表完成了关键字到地址的映射，可以在常数级时间复杂度内通过关键字查找到数据。

至于实现细节，比如用了哪个哈希函数，用了什么冲突处理，甚至某个数据记录的哈希地址是多少，都是不需要开发者关注的。接下来，我们从实际的开发角度，来看一下哈希表对数据的增删查操作。

哈希表中的增加和删除数据操作，不涉及增删后对数据的挪移问题（数组需要考虑），因此处理就可以了。

哈希表查找的细节过程是：对于给定的 key，通过哈希函数计算哈希地址 H (key)。

• 如果哈希地址对应的值为空，则查找不成功。
• 反之，则查找成功。

虽然哈希表查找的细节过程还比较麻烦，但因为一些高级语言的黑盒化处理，开发者并不需要实际去开发底层代码，只要调用相关的函数就可以了。

3.2 哈希表的优缺点

• 优势：它可以提供非常快速的插入-删除-查找操作，无论多少数据，插入和删除值需要接近常量的时间。在查找方面，哈希表的速度比树还要快，基本可以瞬间查找到想要的元素。
• 不足：哈希表中的数据是没有顺序概念的，所以不能以一种固定的方式（比如从小到大）来遍历其中的元素。在数据处理顺序敏感的问题时，选择哈希表并不是个好的处理方法。同时，哈希表中的
  key 是不允许重复的，在重复性非常高的数据中，哈希表也不是个好的选择。

四、 设计哈希映射

4.1 设计要求

要求：

不使用任何内建的哈希表库设计一个哈希映射具体地说，设计应该包含以下的功能：

• put(key, value)：向哈希映射中插入(键,值)的数值对。如果键对应的值已经存在，更新这个值。
• get(key)：返回给定的键所对应的值，如果映射中不包含这个键，返回-1。
• remove(key)：如果映射中存在这个键，删除这个数值对。

示例：

MyHashMap hashMap = new MyHashMap();
hashMap.put(1, 1); hashMap.put(2, 2); hashMap.get(1); // 返回 1
hashMap.get(3); // 返回 -1 (未找到)
hashMap.put(2, 1); // 更新已有的值
hashMap.get(2); // 返回 1 
hashMap.remove(2); // 删除键为2的数据
hashMap.get(2); // 返回 -1 (未找到)

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
 

注意：

 所有的值都在 [0, 1000000]的范围内。
 操作的总数目在[1, 10000]范围内。
 不要使用内建的哈希库。

  

 

  
1
  
2
  
3
 

4.2 设计思路

哈希表是一个在不同语言中都有的通用数据结构。例如，Python 中的 dict 、C++中的 map 和 Java 中的 Hashmap。哈希表的特性是可以根据给出的 key 快速访问 value。

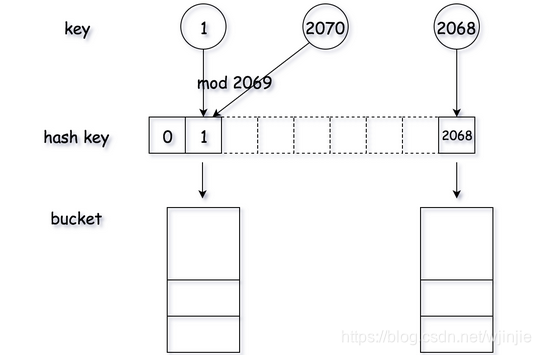
最简单的思路就是用模运算作为哈希方法，为了降低哈希碰撞的概率，通常取素数的模，例如 模 2069。

定义 array 数组作为存储空间，通过哈希方法计算数组下标。为了解决 哈希碰撞 （即键值不同，但映射下标相同），利用桶来存储所有对应的数值。桶可以用数组或链表来实现，在下面的具体实现中， Python 中用的是数组。

定义哈希表方法，get()，put() 和 remove()，其中的寻址过程如下所示：

• 对于一个给定的键值，利用哈希方法生成键值的哈希码，利用哈希码定位存储空间。对于每个哈希码，都能找到一个桶来存储该键值所对应的数值。
• 在找到一个桶之后，通过遍历来检查该键值对是否已经存在。

4.3 实际案例

Python实现如下：

class Bucket: def __init__(self): self.bucket = [] def get(self, key): for (k, v) in self.bucket: if k == key: return v return -1 def update(self, key, value): found = False for i, kv in enumerate(self.bucket): if key == kv[0]: self.bucket[i] = (key, value) found = True break if not found: self.bucket.append((key, value)) def remove(self, key): for i, kv in enumerate(self.bucket): if key == kv[0]: del self.bucket[i]


class MyHashMap(object): def __init__(self): """ Initialize your data structure here. """ # better to be a prime number, less collision self.key_space = 2069 self.hash_table = [Bucket() for i in range(self.key_space)] def put(self, key, value): """ value will always be non-negative. :type key: int :type value: int :rtype: None """ hash_key = key % self.key_space self.hash_table[hash_key].update(key, value) def get(self, key): """ Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key :type key: int :rtype: int """ hash_key = key % self.key_space return self.hash_table[hash_key].get(key) def remove(self, key): """ Removes the mapping of the specified value key if this map contains a mapping for the key :type key: int :rtype: None """ hash_key = key % self.key_space self.hash_table[hash_key].remove(key)


# Your MyHashMap object will be instantiated and called as such:
# obj = MyHashMap()
# obj.put(key,value)
# param_2 = obj.get(key)
# obj.remove(key)


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
  
60
  
61
  
62
  
63
  
64
  
65
  
66
  
67
  
68
  
69
  
70
  
71
  
72
  
73
  
74
  
75
 

复杂度分析：

• 时间复杂度：每个方法的时间复杂度都为 O(N/K)，其中 N 为所有可能键值的数量，K 为哈希表中预定义桶的数量，在这里 K 为 2069。这里我们假设键值是均匀地分布在所有桶中的，桶的平均大小为 N/K​，在最坏情况下需要遍历完整个桶，因此时间复杂度为 O(N/K)。
• 空间复杂度：O(K+M)，其中 K 为哈希表中预定义桶的数量，M 为哈希表中已插入键值的数量。

今天的分享就到这里啦，希望对你的学习有所帮助！

养成习惯，先赞后看！你的支持是我创作的最大动力！

文章来源: ai-wx.blog.csdn.net，作者：AI 菌，版权归原作者所有，如需转载，请联系作者。

原文链接：ai-wx.blog.csdn.net/article/details/108773366