【最小路径和】系列汇总，持续更新！

一、最小路径和（LeetCode 64）

题目

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，
使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-path-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
 

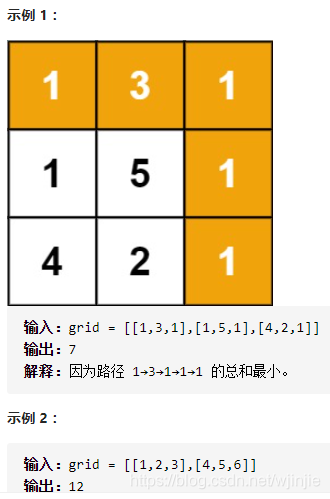
解析

考察从左上角到右下角的最短路径，这是一道经典的动态规划题。因此，确定状态方程，以及边界很重要，下面来一一分析。

问题分析：

由于路径的方向只能是向下或向右，因此网格的第一行的每个元素只能从左上角元素开始向右移动到达，网格的第一列的每个元素只能从左上角元素开始向下移动到达。

对于不在第一行和第一列的元素，可以从其上方相邻元素向下移动一步到达，或者从其左方相邻元素向右移动一步到达，元素对应的最小路径和等于其上方相邻元素与其左方相邻元素两者对应的最小路径和中的最小值加上当前元素的值。

确定初始条件以及状态转移方程：

首先，创建二维数组 dp，与原始网格的大小相同，dp[i][j] 表示从左上角出发到 (i,j) 位置的最小路径和。显然，初始条件满足：dp[0][0] = grid[0][0]。

对于 dp 中的其余元素，通过以下状态转移方程计算元素值：

• 当 i>0，且 j=0 时，dp[i][0] = dp[i-1][0] + grid[i][0]
• 当 j>0，且 i=0 时，dp[0][j] = dp[0][j-1] + grid[0][j]
• 当 i>0，且 j>0 时，dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]

最后得到 dp[m−1][n−1] 的值即为从网格左上角到网格右下角的最小路径和。

C++实现如下：

class Solution {
public: int minPathSum(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); if(!m||!n) return 0; auto dp = vector < vector <int> > (m, vector <int> (n)); dp[0][0] = grid[0][0]; for(int i=1; i<m; ++i) dp[i][0] = dp[i-1][0] + grid[i][0]; for(int j=1; j<n; ++j) dp[0][j] = dp[0][j-1] + grid[0][j]; for(int i=1; i<m; ++i) for(int j=1; j<n; ++j) dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]; return dp[m-1][n-1]; }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

提交结果：

二、下降路径最小和（LeetCode 931）

题目

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径的最小和 。
下降路径可以从第一行中的任何元素开始，并从每一行中选择一个元素。
在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。
具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

提示：
n == matrix.length
n == matrix[i].length
1 <= n <= 100
-100 <= matrix[i][j] <= 100

链接：https://leetcode-cn.com/problems/minimum-falling-path-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

题解

class Solution {
public: int minFallingPathSum(vector<vector<int>>& A) { //从下到上 int n=A.size(),rec; for(int i=n-2;i>=0;--i) for(int j=0;j<n;++j) { rec=A[i+1][j]; if(j>0) rec=min(rec,A[i+1][j-1]); if(j<n-1) rec=min(rec,A[i+1][j+1]); A[i][j]+=rec; } return *min_element(A[0].begin(), A[0].end()); }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
 

文章来源: ai-wx.blog.csdn.net，作者：AI 菌，版权归原作者所有，如需转载，请联系作者。

原文链接：ai-wx.blog.csdn.net/article/details/116152346