一、实验目的

学习用 FFT 对连续信号和时域离散信号进行频谱分析（也称谱分析）的方法， 了解可能出现的分析误差及其原因，以便正确应用FFT。

二、实验原理与方法

• 用FFT对信号作频谱分析是学习数字信号处理的重要内容，经常需要进行谱分析的信号是模拟信号和时域离散信号，对信号进行谱分析的重要问题是频谱分辨率 D 和分析误差。
• 频谱分辨率直接和 FFT 的变换区间 N 有关，因为FFT能够实现的频率分辨率是2π/N，因此要求2π/N≤D。可以根据此式选择 FFT 的变换区间N。误差主要来自于用 FFT 作频谱分析时，得到的是离散谱，而信号（周期信号除外）是连续谱，只有当 N 较大时离散谱的包络才能逼近于连续谱，因此 N 要适当选择大一些。
• 周期信号的频谱是离散谱，只有用整数倍周期的长度作FFT，得到的离散谱才能代表周期信号的频谱。如果不知道信号周期，可以尽量选择信号的观察时间长一些。
• 对模拟信号进行谱分析时，首先要按照采样定理将其变成时域离散信号。如果是模拟周期信号，也应该选取整数倍周期的长度，经过采样后形成周期序列，按照周期序列的谱分析进行。

三、实验内容及步骤

1. 有限长序列

选择 FFT 的变换区间 N 为 8 和 16 的两种情况进行频谱分析。分别打印其幅频特性曲线， 并进行对比、 分析和讨论。

%R4(n)的谱分析   有限长序列
%做N点DFT  不够的话  时域补零到N点
%8点->16点  相邻谱线间隔变密  离散谱的包络更接近于连续谱
clear;

x1=[1 1 1 1];
%8点DFT
N1=8;
xk=fft(x1,N1);   %计算x1(n)的8点DFT
subplot(221); stem(0:N1-1,[x1 zeros(1,N1-4)],'.','g'); %时域补零到 8个点 绘图
xlabel('n');
ylabel('x(n)');
title('R4(n)');
axis([0 8 0 1.2]);

subplot(222);
stem(0:0.25:1.75,abs(xk),'.','g'); xlabel('\omega/\pi');
ylabel('幅度');
title('8点DFT的结果');
axis([0 2 0 4.5]);

%16点DTF
N2=16;
xk=fft(x1,N2);
subplot(223); stem(0:N2-1,[x1 zeros(1,N2-4)],'.','r'); %时域补零到16个点 绘图
xlabel('n');
ylabel('x(n)');
title('R4(n)');
axis([0 16 0 1.2]);

subplot(224);
stem(0:0.125:1.875,abs(xk),'.','r');  
xlabel('\omega/\pi');
ylabel('幅度');
title('16点DFT的结果');
axis([0 2 0 4.5]);

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
 

运行效果如下：

%x2(n)的谱分析
%做N点DFT  不够的话  时域补零到N点

clear;

x2=[1 2 3 4 4 3 2 1];

%8点DFT
N1=8;
subplot(221); stem(0:N1-1,x2,'.','g'); 
xlabel('n');
ylabel('x(n)');
title('x2(n)');
axis([0 8 0 4.5]);

xk=fft(x2,N1);
subplot(222);
stem(0:0.25:1.75,abs(xk),'.','g');   %归一化
xlabel('\omega/\pi');
ylabel('幅度');
title('8点DFT的结果');
axis([0 2 0 24]);

%16点DFT
N2=16;
subplot(223); stem(0:N2-1,[x2 zeros(1,N2-8)],'.','r');  %时域补零到16点
xlabel('n');
ylabel('x(n)');
title('x2(n)');
axis([0 16 0 4.5]);

xk=fft(x2,N2);
subplot(224);
stem(0:0.125:1.875,abs(xk),'.','r');
xlabel('\omega/\pi');
ylabel('幅度');
title('16点DFT的结果');
axis([0 2 0 24]);


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
 

运行效果如下：

%x3(n)的频谱分析
%做N点DFT  不够的话  时域补零到N点
clear;

x3=[4 3 2 1 1 2 3 4];

%8点DFT
N1=8;
subplot(221); stem(0:N1-1,x3,'.','g'); 
xlabel('n');
ylabel('x(n)');
title('x3(n)');
axis([0 8 0 4.5]);
xk=fft(x3,N1);
subplot(222);
stem(0:0.25:1.75,abs(xk),'.','g');
xlabel('\omega/\pi');
ylabel('幅度');
title('8点DFT的结果');
axis([0 2 0 24]);

%16点DFT
N2=16;
subplot(223); stem(0:N2-1,[x3 zeros(1,N2-8)],'.','r'); %时域补零到16点
xlabel('n');
ylabel('x(n)');
title('x3(n)');
axis([0 16 0 4.5]);
xk=fft(x3,N2);
subplot(224);
stem(0:0.125:1.875,abs(xk),'.','r');
xlabel('\omega/\pi');
ylabel('幅度');
title('16点DFT的结果');
axis([0 2 0 24]);

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
 

运行效果如下：

观察可以发现：

• 由 MATLAB 绘图可以发现，N=8时，x2(n) 和 x3(n) 的幅频特性是相同的，因为x2(n)=x3((n-4))R8(n)，循环移位关系，所以 x3(n) 与 x2(n) 的 DFT 的幅频特性相同，如图 (2a) 和 (3a) 所示
• 但是，当 N=16时，x3(n) 与 x2(n) 就不满足循环移位关系了，所以如图 (2b) 和 (3b) 所示，幅频特性不同

2. 周期序列

选择 FFT 的变换区间 N 为 8 和 16 的两种情况分别对以上序列进行频谱分析，分别打印其幅频特性曲线。 并进行对比、分析和讨论。

%x4(n)=cos(pi/4*n)的频谱分析   周期序列 
%周期序列x(n)周期如果事先不知道 截取M点进行DFT  再将截取长度扩大一倍
%比较二者主谱差别 若满足分析误差要求  这两个都可以近似表示x(n)的频谱
%否则  继续将截取长度加倍  直到前后两次主谱差别满足误差要求
%幅度跟N有关  主瓣会变窄 旁瓣会增加  更接近于真实的频谱 幅度是冲激那样的 又窄又高
clear;

n=0:31;
x4=cos(pi/4*n);

%8点DFT
N1=8;
subplot(221); stem(0:1:31,x4,'.','g'); 
xlabel('n');
ylabel('x(n)');
title('x4(n)');
axis([0 31 -1.2 1.2]);

xk=fft(x4,N1);
subplot(222);
stem(0:0.25:1.75,abs(xk),'.','g');
xlabel('\omega/\pi');
ylabel('幅度');
title('8点DFT的结果');
axis([0 2 0 5]);

%16点DFT
N2=16;
subplot(223); stem(0:1:31,x4,'.','r'); 
xlabel('n');
ylabel('x(n)');
title('x4(n)');
axis([0 31 -1.2 1.2]);

xk=fft(x4,N2);
subplot(224);
stem(0:0.125:1.875,abs(xk),'.','r');
xlabel('\omega/\pi');
ylabel('幅度');
title('16点DFT的结果');
axis([0 2 0 9]);

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
 

运行效果如下：

%x5(n)=cos(pi/4*n)+cos(pi/8*n)的频谱分析
%周期序列x(n)周期如果事先不知道 截取M点进行DFT  再将截取长度扩大一倍
%比较二者主谱差别满足分析误差要求  这两个都可以近似表示x(n)的频谱
%否则  继续将截取长度加倍  直到前后两次主谱差别满足误差要求
clear;

n=0:31;
x5=cos(pi/4*n)+cos(pi/8*n);

%8点DFT
N1=8;
subplot(321); stem(0:1:31,x5,'.','m'); 
xlabel('n');
ylabel('x(n)');
title('x5(n)');
axis([0 31 -2.2 2.5]);

xk=fft(x5,N1);
subplot(322);
stem(0:0.25:1.75,abs(xk),'.','m');
xlabel('\omega/\pi');
ylabel('幅度');
title('8点DFT的结果');
axis([0 2 0 7]);

%16点DFT
N2=16;
subplot(323); stem(0:1:31,x5,'.','r'); 
xlabel('n');
ylabel('x(n)');
title('x5(n)');
axis([0 31 -2.2 2.5]);

xk=fft(x5,N2);
subplot(324);
stem(0:0.125:1.875,abs(xk),'.','r');
xlabel('\omega/\pi');
ylabel('幅度');
title('16点DFT的结果');
axis([0 2 0 10]);

%32点DFT
N2=32;
subplot(325); stem(0:1:31,x5,'.','g'); 
xlabel('n');
ylabel('x(n)');
title('x5(n)');
axis([0 31 -2.2 2.5]);

xk=fft(x5,N2);
subplot(326);
stem(0:0.0625:1.9375,abs(xk),'.','g');
xlabel('\omega/\pi');
ylabel('幅度');
title('32点DFT的结果');
axis([0 2 0 20]);

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
  
59
 

运行效果如下：

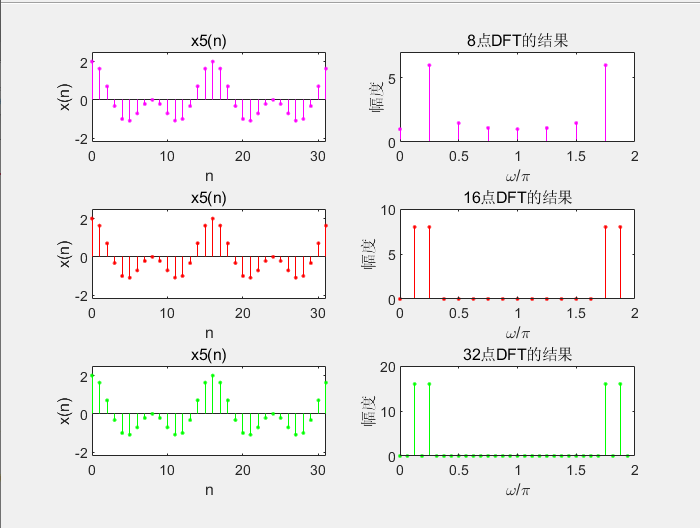
• 对周期序列 x(n) 进行谱分析，如果事先不知道周期，可以先截取 M 点进行DFT ，再将截取长度扩大一倍，比较结果，如果二者的差别满足分析误差要求，则可以近似表示该信号的频谱，如果不满足误差要求就继续将截取长度加倍，重复比较，直到结果满足要求。
• 幅度为N/2，N增大，主瓣会变窄，旁瓣会增加 ，更接近于真实的频谱，幅度是冲激那样的，又窄又高。

3. 模拟周期信号

%对模拟周期信号作谱分析  
%首先要按照采样定理将其变成时域离散信号
%如果是模拟周期信号， 也应该选取整数倍周期的长度， 经过采样后形成周期序列
%再按照周期序列的谱分析进行
clear;

Fs=64;T=1/Fs;

%先按照采样定理将模拟信号变成时域离散信号
N=16;n=0:N-1; %FFT的变换区间 N=16
x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T); %对x6(t) 16点采样

%fftshift移动零频点到频谱中间 为了把结果和fft运算的结果一致
X6k16=fftshift(fft(x6nT,16)); %计算 x6nT 的16点 DFT  
Tp=N*T;F=1/Tp; %频率分辨率 F
k=0:N-1;fk1=-32:4:28; %产生16点 DFT 对应的采样点频率（以零频率为中心）
subplot(3,1,1);stem(fk1,abs(X6k16),'.','g'); %绘制16点DFT的幅频特性图
title('16点 DFT[x_6(nT)]|');xlabel('\omega/\pi');ylabel('幅度');
axis([-32 28 0 12]);

N=32;n=0:N-1; %FFT 的变换区间 N=32
x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T); %对 x6(t) 32点采样
X6k32=fftshift(fft(x6nT,32)); %计算x6(nT)的 32 点 DFT
Tp=N*T;F=1/Tp; %频率分辨率 F
k=0:N-1;fk2=-32:2:30; %产生 32 点 DFT 对应的采样点频率（以零频率为中心）
subplot(3,1,2);stem(fk2,abs(X6k32),'.','r'); %绘制 32 点 DFT 的幅频特性图
title('32点 DFT[x_6(nT)]|');xlabel('\omega/\pi');ylabel('幅度');
axis([-32 31 0 20]);

N=64;n=0:N-1; %FFT 的变换区间 N=64
x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T); %对x6(t) 64点采样
X6k64=fftshift(fft(x6nT,64)); %计算 x6(nT) 的64点DFT
Tp=N*T;F=1/Tp; %频率分辨率 F
k=0:N-1;fk3=-32:1:31; %产生64点 DFT对应的采样点频率（以零频率为中心）
subplot(3,1,3);stem(fk3,abs(X6k64),'.','m'); %绘制64点DFT的幅频特性图
title('64点 DFT[x_6(nT)]|');xlabel('\omega/\pi');ylabel('幅度');
axis([-32 31 0 40]);


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
 

运行效果如下：

四、回答思考题

（1） 对于周期序列， 如果周期不知道， 如何用 FFT 进行谱分析？

答：周期信号的周期预先不知道时，可先截取 M 点进行DFT，再将截取长度扩大一倍截取，比较结果，如果二者的差别满足分析误差要求,则可以近似表示该信号的频谱，如果不满足误差要求就继续将截取长度加倍，重复比较，直到结果满足要求。

（2） 如何选择FFT的变换区间（包括非周期信号和周期信号）？

答：对于非周期信号：有频谱分辨率F，而频谱分辨率直接和 FFT 的变换区间有关，因为 FFT 能够实现的频率分辨率是2π/N…因此有最小的N>2π/F。就可以根据此式选择 FFT 的变换区间。对于周期信号，周期信号的频谱是离散谱，只有用整数倍周期的长度作FFT，得到的离散谱才能代表周期信号的频谱。

（3）当 N=8 时， x2 (n) 和 x3 (n)的幅频特性会相同吗？为什么？N=16时呢？

• 由 MATLAB 绘图可以发现，N=8时，x2(n) 和 x3(n) 的幅频特性是相同的，因为x3(n)=x2((n+4))R8(n)，为循环移位关系，所以 x3(n) 与 x2(n) 的DFT的幅频特性相同，如图 (2a) 和 (3a) 所示
• 但是，当 N=16 时，x3(n) 与 x2(n) 就不满足循环移位关系了，所以如图 (2b) 和 (3b) 所示，幅频特性不同

五、实验总结

• 用 FFT 对信号作频谱分析是学习数字信号处理的重要内容，经常需要进行谱分析的信号是模拟信号和时域离散信号，对信号进行谱分析的重要问题是频谱分辨率 D 和分析误差。
• 频谱分辨率直接和 FFT 的变换区间 N 有关，因为FFT能够实现的频率分辨率是2π/N，因此要求2π/N≤D。可以根据此式选择 FFT 的变换区间N。误差主要来自于用 FFT 作频谱分析时，得到的是离散谱，而信号（周期信号除外）是连续谱，只有当 N 较大时离散谱的包络才能逼近于连续谱，因此 N 要适当选择大一些。
• 周期信号的频谱是离散谱，只有用整数倍周期的长度作FFT，得到的离散谱才能代表周期信号的频谱。如果不知道信号周期，可以尽量选择信号的观察时间长一些。
• 对模拟信号进行谱分析时，首先要按照采样定理将其变成时域离散信号。如果是模拟周期信号，也应该选取整数倍周期的长度，经过采样后形成周期序列，按照周期序列的谱分析进行。

文章来源: yetingyun.blog.csdn.net，作者：叶庭云，版权归原作者所有，如需转载，请联系作者。

原文链接：yetingyun.blog.csdn.net/article/details/109473805