手撕二叉树的4种遍历:前序、中序、后序、层序
相关文章:
- 二叉树的基础知识:什么是树、二叉树、二叉查找树?
- 二叉树专题汇总:二叉树系列汇总,持续更新!
一、构造二叉树
struct TreeNode {
int val; TreeNode *left; TreeNode *right; TreeNode() : val(0), left(nullptr), right(nullptr) {} TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
二、前序遍历
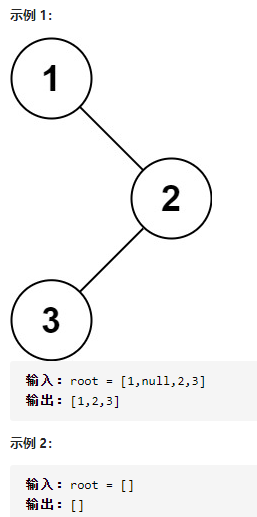
给你二叉树的根节点 root ,返回它节点值的前序遍历。
- 1
C++实现:
首先我们需要了解什么是二叉树的前序遍历:按照访问根节点——左子树——右子树的方式遍历这棵树,而在访问左子树或者右子树的时候,我们按照同样的方式遍历,直到遍历完整棵树。因此整个遍历过程天然具有递归的性质,我们可以直接用递归函数来模拟这一过程。
方法一: 该方法在递归过程中会多次返回ans,但最终输出的ans会覆盖之前的ans,这无形之间增加了内存的开销。
class Solution {
public: vector<int> ans; vector<int> preorderTraversal(TreeNode* root) { if(root != nullptr) { ans.push_back(root->val); preorderTraversal(root->left); preorderTraversal(root->right); } return ans; }
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
提交结果:

方法二:单独创建一个preorder函数进行递归,不断将二叉树的值按照前序遍历的顺序存入数组temp中,需要注意的是,preorder()中的temp要以引用的方式进行声明。
class Solution {
public: void preorder(TreeNode* root, vector<int> &temp) { if(root==nullptr) return; temp.push_back(root->val); preorder(root->left, temp); preorder(root->right, temp); } vector<int> preorderTraversal(TreeNode* root) { vector<int> ans; preorder(root, ans); return ans; }
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
提交结果:

三、中序遍历
二叉树的中序遍历:按照访问左子树——根节点——右子树的方式遍历这棵树,而在访问左子树或者右子树的时候,我们按照同样的方式遍历,直到遍历完整棵树。因此整个遍历过程天然具有递归的性质,我们可以通过创建递归函数 inorder() 来模拟这一过程。
C++实现如下所示:
class Solution {
public: void inorder(TreeNode* root, vector<int> &temp) { if(root==nullptr) return; inorder(root->left, temp); temp.push_back(root->val); inorder(root->right, temp); } vector<int> inorderTraversal(TreeNode* root) { vector<int> ans; inorder(root, ans); return ans; }
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
提交结果:

四、后序遍历
二叉树的后序遍历:按照访问左子树——右子树——根节点的方式遍历这棵树,而在访问左子树或者右子树的时候,我们按照同样的方式遍历,直到遍历完整棵树。因此整个遍历过程天然具有递归的性质,我们可以通过创建递归函数 inorder() 来模拟这一过程。
C++实现如下所示:
class Solution {
public: void postorder(TreeNode* root, vector<int> &temp) { if(root==nullptr) return; postorder(root->left, temp); postorder(root->right, temp); temp.push_back(root->val); } vector<int> postorderTraversal(TreeNode* root) { vector<int> ans; postorder(root, ans); return ans; }
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
提交结果:

五、层序遍历
给你一个二叉树,请你返回其按层序遍历得到的节点值。(即逐层地,从左到右访问所有节点)。
- 1

分析: 在二叉树的各种遍历之中,通常都会用到深度优先搜索(DFS)或者广度优先搜索(BFS)。在二叉树的前序、中序、后序遍历之中,我们采用的是DFS,即用递归的思想来遍历整个二叉树结构。而对于层序遍历,只能使用 BFS 进行遍历。
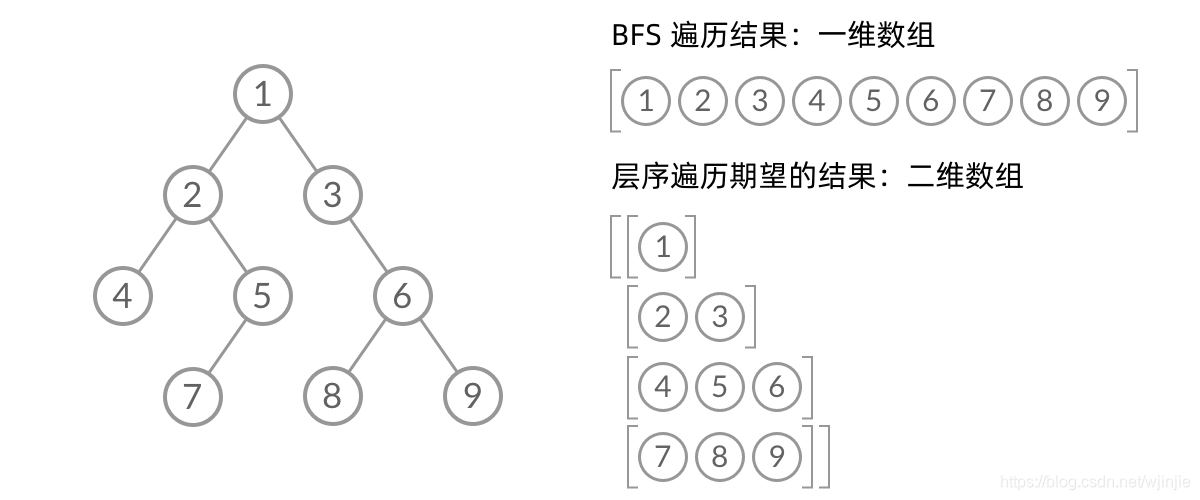
么是层序遍历呢?简单来说,层序遍历就是把二叉树分层,然后每一层从左到右遍历:

乍一看,这个遍历顺序和 BFS 是一样的,我们可以直接用 BFS 得出层序遍历结果。然而,层序遍历要求的输入结果和 BFS 是不同的。层序遍历要求我们区分每一层,也就是返回一个二维数组。 而 BFS 的遍历结果是一个一维数组,无法区分每一层。如下图所示:
因此,在每一层遍历开始前,需要先记录队列中的结点数量 n(也就是这一层的结点数量),然后通过 for 循环处理完这一层的 n 个结点。这个处理部分需要两个任务:
- 将该层节点的值,依次存入该层的数组之中。
- 将该层的所有节点的左、右子树依次存入队列中,这些节点待下一次再依次进行相同的处理。
注意:在 BFS 中,之所以选用队列存放节点,是因为其具有先进先出的性质,这种性质能非常方便地对节点按顺序的取出(q.front())和删除(q.pop())。
采用广度优先搜索实现如下:
class Solution {
public: vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>> ans; if(root==nullptr) return ans; queue<TreeNode*> q; q.push(root); while(!q.empty()) { int n = q.size(); // 二叉树当前层节点的个数 ans.push_back(vector<int> ()); //初始化当前层的空数组 for(int i=0; i<n; ++i) { // 将队列中节点的值存入到该层的数组中 TreeNode* node = q.front(); q.pop(); ans.back().push_back(node->val); // 将下一层的节点存入到队列中 if(node->left!=nullptr) q.push(node->left); if(node->right!=nullptr) q.push(node->right); } } return ans; }
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
由于水平有限,博客中难免会有一些错误,有纰漏之处恳请各位大佬不吝赐教!

最好的关系是互相成就,各位的「三连」就是【AI 菌】创作的最大动力,我们下期见!
文章来源: ai-wx.blog.csdn.net,作者:AI 菌,版权归原作者所有,如需转载,请联系作者。
原文链接:ai-wx.blog.csdn.net/article/details/116429112
- 点赞
- 收藏
- 关注作者


评论(0)