快速排序——寻找数组第K大数（由浅入深，四种方法对比讲解！）

寻找数组第K大数是大厂面试中经常考到的一题，有的小机灵鬼直接用sort()进行排序，两行代码解决，这样看似可行，实则掉入了出题人的陷阱。面试官希望看到的是你对算法的理解，而不是函数的调用。下面，我就以本题为例，由浅入深，用四种方法来分别解决此题，最后推荐的是快速排序，这里先给出快速排序的动态演示图，具体讲到思路以及实现详见文中！

题目：寻找第K大

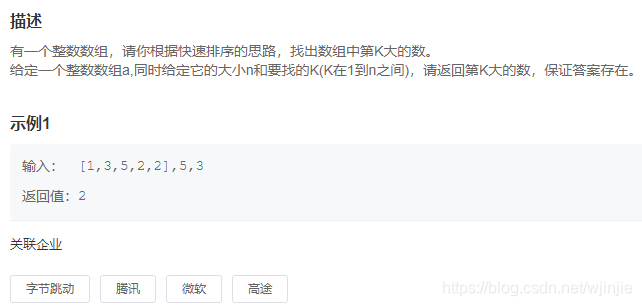
方法一：全局排序

使用C++中内置函数sort进行全局排序，再取第K大值：

class Solution {
public: int findKth(vector<int> a, int n, int K) { sort(a.begin(), a.end()); return a[n-K]; }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

提交结果：

方法二：局部排序

使用冒泡排序的思想，每次将最大的值放在数组尾部，直到第K个，时间复杂度O(nk)：

class Solution {
public: int findKth(vector<int> a, int n, int K) { for(int i=0; i<K; ++i) { for(int j=0; j<n-i-1; ++j) { if(a[j]>a[j+1]) { int temp = a[j]; a[j] = a[j+1]; a[j+1] = temp; } } } return a[n-K]; }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
 

提交结果：

方法三：优先队列

最小堆的方式实现，有关堆与优先队列的关系，可参考：堆和优先队列

class Solution {
public: int findKth(vector<int> a, int n, int K) { priority_queue <int, deque<int>, greater<int>> nums; //队首最小,从小到大排序 for(int i=0; i<n; ++i) { if(i<K) { nums.push(a[i]); } else { if(a[i]>nums.top()) { nums.pop(); nums.push(a[i]); } } } return nums.top(); }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

提交结果：

方法四：快速排序

快排思想：通过一趟排序将待排序元素分成独立的两部分，其中一部分记录的元素均比另一部分记录的元素要小，则可分别对这两部分记录继续进行排序，直到整个序列有序为止。具体做法如下：

1. 首先选取基准元素base（首元素，中间元素，最后元素，随机元素等等）。
2. 以基准元素为基准，将小于基准元素的元素放在前面，大于基准元素的放在后面。
3. 然后以基准元素为界限，分为两组数据。
4. 两组元素重复1、2和3步骤，直至比较排序完成。

快排的最坏运行时间为O(n^2)，平均运行时间为O(nlogn)。由于跳跃式交换比较，故不稳定！动态演示过程如下：

快速排序的C++实现方法如下：

vector<int> quickSort(vector<int>&nums, int start, int end)
{
	if (start >= end) return nums;
	int base = nums[start];
	int i = start;
	int j = end;
	while (i < j)
	{ while (i < j && nums[j] >= base) j--; //从右往左，寻找比base小的数 swap(nums[i], nums[j]); //找到比base小的数，即与base交换位置 while (i < j && nums[i] <= base) i++; //从左往右，寻找比base大的数 swap(nums[i], nums[j]); //找到比base大的数，即与base交换位置
	}
	quickSort(nums, start, i - 1);
	quickSort(nums, i + 1, end);
	return nums;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
 

对于本题，可以先采用快排的方法进行全局排序，然后直接返回第K大即可：

class Solution {
public: vector<int> quickSort(vector<int>&nums, int start, int end) { if (start >= end) return nums; int base = nums[start]; int i = start; int j = end; while (i < j) { while (i < j && nums[j] >= base) j--; //从右往左，寻找比base小的数 swap(nums[i], nums[j]); //找到比base小的数，即与base交换位置 while (i < j && nums[i] <= base) i++; //从左往右，寻找比base大的数 swap(nums[i], nums[j]); //找到比base大的数，即与base交换位置 } quickSort(nums, start, i - 1); quickSort(nums, i + 1, end); return nums; } int findKth(vector<int> a, int n, int K) { quickSort(a, 0, n-1); return a[n-K]; }
};


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
 

显然，这不是最佳结果。我们进一步考虑，发现在快排过程中，如果在base右边的元素个数超过K个，那么结果肯定在base右边，左边的元素就可以不考虑再去排序了。因此，在迭代过程中，我们加一句判断，这样计算的时间复杂度就能进一步减小。如下所示：

class Solution {
public: vector<int> quickSort(vector<int>&nums, int start, int end, int K) { if (start >= end) return nums; int base = nums[start]; int i = start; int j = end; while (i < j) { while (i < j && nums[j] >= base) j--; //从右往左，寻找比base小的数 swap(nums[i], nums[j]); while (i < j && nums[i] <= base) i++; swap(nums[i], nums[j]); } if(nums.size()-i<K) //如果base右边的数超过K个，则第K大数肯定在base右边，此时就不需要对base左边的进行排序 quickSort(nums, start, i - 1, K); quickSort(nums, i + 1, end, K); return nums; } int findKth(vector<int> a, int n, int K) { quickSort(a, 0, n-1, K); return a[n-K]; }
};


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
 

最后的提交结果：

参考链接：

• C实现快速排序：https://www.runoob.com/w3cnote/quick-sort.html
• Python实现快速排序：https://minenet.me/2016/08/24/quickSort.html

文章来源: ai-wx.blog.csdn.net，作者：AI 菌，版权归原作者所有，如需转载，请联系作者。

原文链接：ai-wx.blog.csdn.net/article/details/117480013