回溯算法之布罗夫卫队(最大团问题)
【摘要】 1、问题
在原始部落中,由于食物缺乏,部落居民经常因为争夺猎物发生冲突,几乎每个居民都 有自己的仇敌。部落酋长为了组织一支保卫部落的卫队,希望从居民中选出最多的居民加入 卫队,并保证卫队中任何两个人都不是仇敌。假设已给定部落中居民间的仇敌关系图,编程 计算构建部落护卫队的最佳方案。
2、分析
以部落中的 5 个居民为例,我们把每个居民编号作为...
1、问题
在原始部落中,由于食物缺乏,部落居民经常因为争夺猎物发生冲突,几乎每个居民都 有自己的仇敌。部落酋长为了组织一支保卫部落的卫队,希望从居民中选出最多的居民加入 卫队,并保证卫队中任何两个人都不是仇敌。假设已给定部落中居民间的仇敌关系图,编程
计算构建部落护卫队的最佳方案。
2、分析
以部落中的 5 个居民为例,我们把每个居民编号作为一个结点,凡是关系友好的两个居
民,就用线连起来,是仇敌的不连线,如图 5-19 所示。国王护卫队问题就转化为从图中找出最多的结点,这些结点相互均有连线(任何两个人都不是仇敌)。
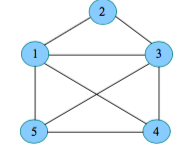
国王护卫队问题属于典型的最大团问题。什么是最大团呢?首先来看什么是团。
完全子图:给定无向图 G=(V,E),其中 V 是结点集,E是边集。G'=(V',E')如果结点集 V'⊆V,E'⊆E,且 G'中任意
两个结点有边相连,则称 G'是 G 的完全子图。其实很简单,G'是 G 的子图,正好
文章来源: chenyu.blog.csdn.net,作者:chen.yu,版权归原作者所有,如需转载,请联系作者。
原文链接:chenyu.blog.csdn.net/article/details/80304796
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)