kaggle房价预测问题
参考:https://blog.csdn.net/m0_37870649/article/details/80979783
sklean的线性模型完成kaggle房价预测问题
https://www.kaggle.com/c/house-prices-Advanced-regression-techniques
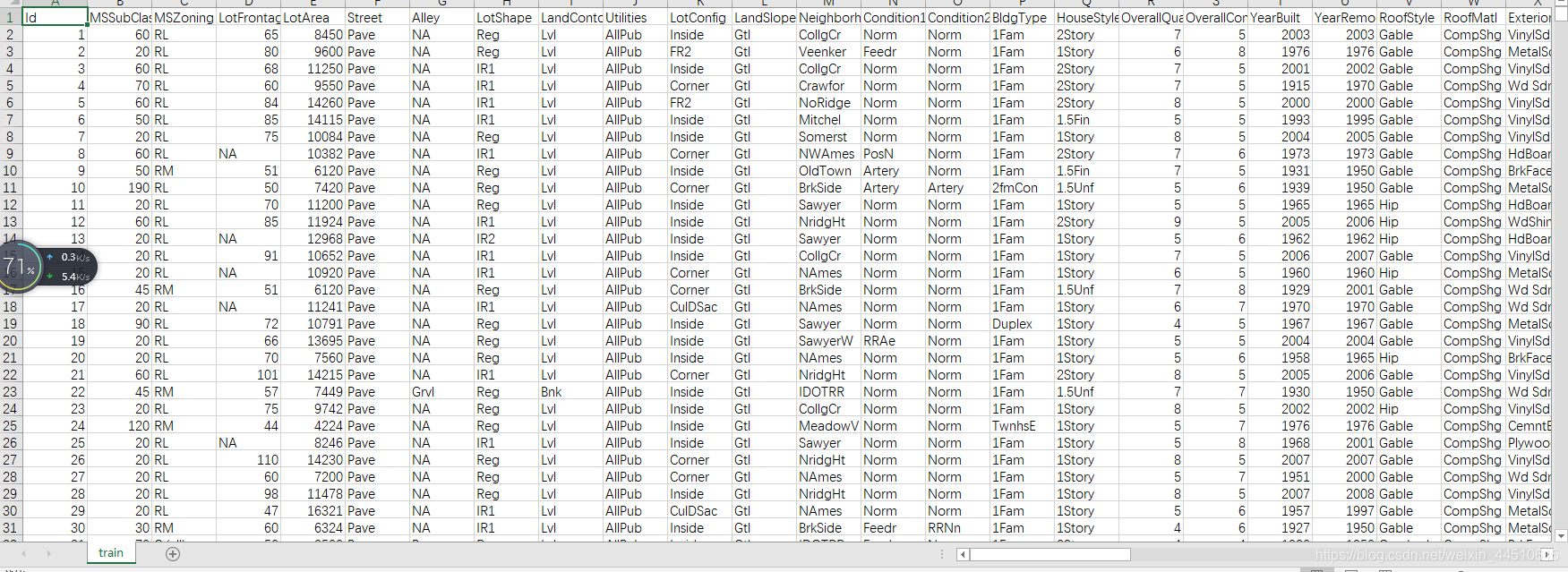
赛题给我们79个描述房屋的特征,要求我们据此预测房屋的最终售价,即对于测试集中每个房屋的ID给出对于的SalePrice字段的预测值,主要考察我们数据清洗、特征工程、模型搭建及调优等方面的技巧。本赛题是典型的回归类问题,评估指标选用的是均方根误差(RMSE),为了使得价格的高低对结果的评估有均等的影响,赛题均方根误差基于预测值和实际值分别取对数对数来计算。
特征初步分析:
1. SalePrice 房屋售价,我们要预测的label,类型:数值型,单位:美元
2. MSSubClass: 建筑的等级,类型:类别型
MSZoning: 区域分类,类型:类别型
LotFrontage: 距离街道的直线距离,类型:数值型,单位:英尺
LotArea: 地皮面积,类型:数值型,单位:平方英尺
Street: 街道类型,类型:类别型
Alley: 巷子类型,类型:类别型
LotShape: 房子整体形状,类型:类别型
LandContour: 平整度级别,类型:类别型
Utilities: 公共设施类型,类型:类别型
LotConfig: 房屋配置,类型:类别型
LandSlope: 倾斜度,类型:类别型
Neighborhood: 市区物理位置,类型:类别型
Condition1: 主干道或者铁路便利程度,类型:类别型
Condition2: 主干道或者铁路便利程度,类型:类别型
BldgType: 住宅类型,类型:类别型
HouseStyle: 住宅风格,类型:类别型
OverallQual: 整体材料和饰面质量,类型:数值型
OverallCond: 总体状况评价,类型:数值型
YearBuilt: 建筑年份,类型:数值型
YearRemodAdd: 改建年份,类型:数值型
RoofStyle: 屋顶类型,类型:类别型
RoofMatl: 屋顶材料,类型:类别型
Exterior1st: 住宅外墙,类型:类别型
Exterior2nd: 住宅外墙,类型:类别型
MasVnrType: 砌体饰面类型,类型:类别型
MasVnrArea: 砌体饰面面积,类型:数值型,单位:平方英尺
ExterQual: 外部材料质量,类型:类别型
ExterCond: 外部材料的现状,类型:类别型
Foundation: 地基类型,类型:类别型
BsmtQual: 地下室高度,类型:类别型
BsmtCond: 地下室概况,类型:类别型
BsmtExposure: 花园地下室墙,类型:类别型
BsmtFinType1: 地下室装饰质量,类型:类别型
BsmtFinSF1: 地下室装饰面积,类型:类别型
BsmtFinType2: 地下室装饰质量,类型:类别型
BsmtFinSF2: 地下室装饰面积,类型:类别型
BsmtUnfSF: 未装饰的地下室面积,类型:数值型,单位:平方英尺
TotalBsmtSF: 地下室总面积,类型:数值型,单位:平方英尺
Heating: 供暖类型,类型:类别型
HeatingQC: 供暖质量和条件,类型:类别型
CentralAir: 中央空调状况,类型:类别型
Electrical: 电力系统,类型:类别型
1stFlrSF: 首层面积,类型:数值型,单位:平方英尺
2ndFlrSF: 二层面积,类型:数值型,单位:平方英尺
LowQualFinSF: 低质装饰面积,类型:数值型,单位:平方英尺
GrLivArea: 地面以上居住面积,类型:数值型,单位:平方英尺
BsmtFullBath: 地下室全浴室,类型:数值
BsmtHalfBath: 地下室半浴室,类型:数值
FullBath: 高档全浴室,类型:数值
HalfBath: 高档半浴室,类型:数值
BedroomAbvGr: 地下室以上的卧室数量,类型:数值
KitchenAbvGr: 厨房数量,类型:数值
KitchenQual: 厨房质量,类型:类别型
TotRmsAbvGrd: 地上除卧室以外的房间数,类型:数值
Functional: 房屋功用性评级,类型:类别型
Fireplaces: 壁炉数量,类型:数值
FireplaceQu: 壁炉质量,类型:类别型
GarageType: 车库位置,类型:类别型
GarageYrBlt: 车库建造年份,类别:数值型
GarageFinish: 车库内饰,类型:类别型
GarageCars: 车库车容量大小,类别:数值型
GarageArea: 车库面积,类别:数值型,单位:平方英尺
GarageQual: 车库质量,类型:类别型
GarageCond: 车库条件,类型:类别型
PavedDrive: 铺的车道情况,类型:类别型
WoodDeckSF: 木地板面积,类型:数值型,单位:平方英尺
OpenPorchSF: 开放式门廊区面积,类型:数值型,单位:平方英尺
EnclosedPorch: 封闭式门廊区面积,类型:数值型,单位:平方英尺
3SsnPorch: 三个季节门廊面积,类型:数值型,单位:平方英尺
ScreenPorch: 纱门门廊面积,类型:数值型,单位:平方英尺
PoolArea: 泳池面积,类型:数值型,单位:平方英尺
PoolQC:泳池质量,类型:类别型
Fence: 围墙质量,类型:类别型
MiscFeature: 其他特征,类型:类别型
MiscVal: 其他杂项特征值,类型:类别型
MoSold: 卖出月份,类别:数值型
YrSold: 卖出年份,类别:数值型
SaleType: 交易类型,类型:类别型
SaleCondition: 交易条件,类型:类别型
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib
import matplotlib.pyplot as plt
from scipy.stats import skew
from scipy.stats.stats import pearsonr
%config InlineBackend.figure_format = 'retina' #set 'png' here when working on notebook
%matplotlib inline
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
- 1
- 2
train.head()
- 1
| Id | MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | ... | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 60 | RL | 65.0 | 8450 | Pave | NaN | Reg | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 2 | 2008 | WD | Normal | 208500 |
| 1 | 2 | 20 | RL | 80.0 | 9600 | Pave | NaN | Reg | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 5 | 2007 | WD | Normal | 181500 |
| 2 | 3 | 60 | RL | 68.0 | 11250 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 9 | 2008 | WD | Normal | 223500 |
| 3 | 4 | 70 | RL | 60.0 | 9550 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 2 | 2006 | WD | Abnorml | 140000 |
| 4 | 5 | 60 | RL | 84.0 | 14260 | Pave | NaN | IR1 | Lvl | AllPub | ... | 0 | NaN | NaN | NaN | 0 | 12 | 2008 | WD | Normal | 250000 |
5 rows × 81 columns
all_data = pd.concat((train.loc[:,'MSSubClass':'SaleCondition'], test.loc[:,'MSSubClass':'SaleCondition']))
- 1
- 2
数据预处理:
我们不会在这里做任何花哨的事情:
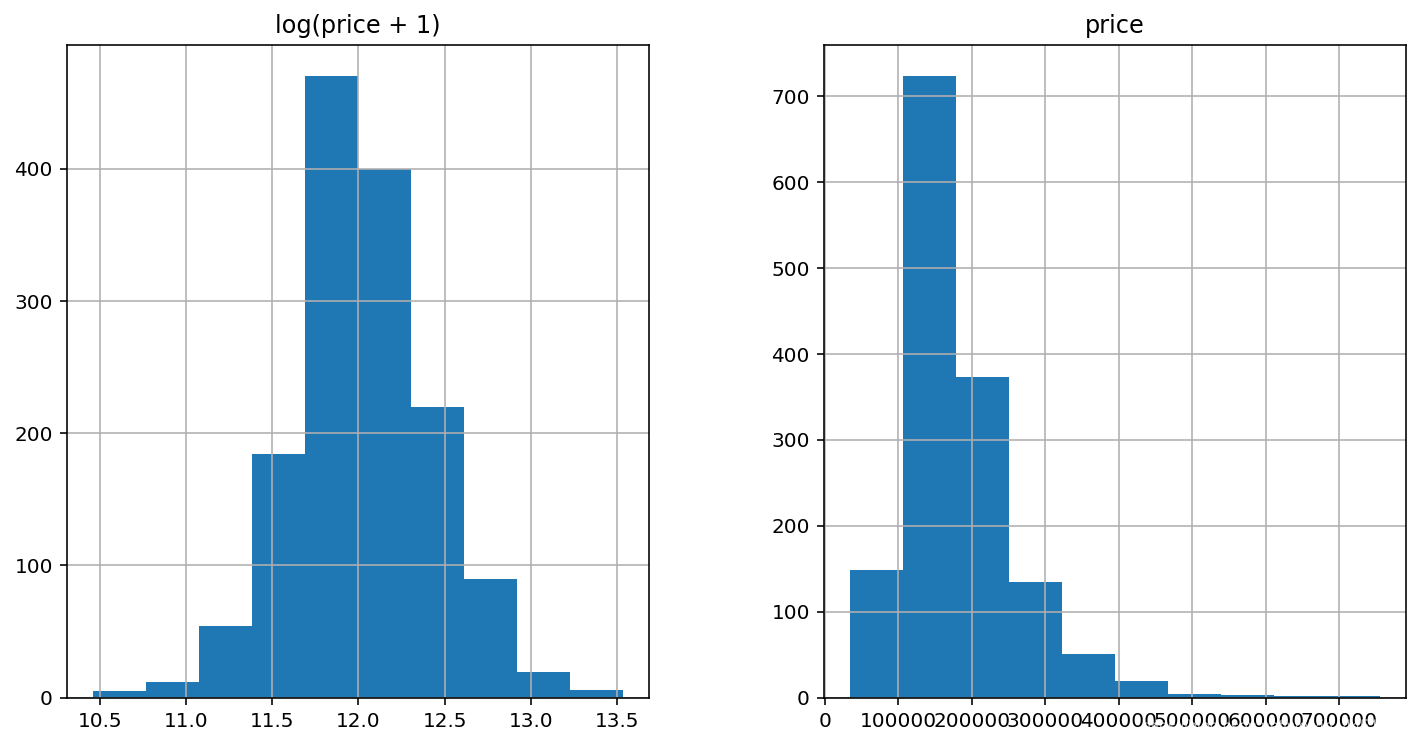
首先,我将通过记录(feature+1)来转换倾斜的数字特性-这将使特性更加正常
为分类特征创建虚拟变量
将数字缺失值(NaN)替换为其各自列的平均值
matplotlib.rcParams['figure.figsize'] = (12.0, 6.0)
prices = pd.DataFrame({"price":train["SalePrice"], "log(price + 1)":np.log1p(train["SalePrice"])})
prices.hist()
- 1
- 2
- 3
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x00000268013A1320>, <matplotlib.axes._subplots.AxesSubplot object at 0x00000268013F20F0>]], dtype=object)
- 1
- 2
- 3
#log transform the target:
train["SalePrice"] = np.log1p(train["SalePrice"])
#log transform skewed numeric features:
numeric_feats = all_data.dtypes[all_data.dtypes != "object"].index
skewed_feats = train[numeric_feats].apply(lambda x: skew(x.dropna())) #compute skewness
skewed_feats = skewed_feats[skewed_feats > 0.75]
skewed_feats = skewed_feats.index
all_data[skewed_feats] = np.log1p(all_data[skewed_feats])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
all_data = pd.get_dummies(all_data)
- 1
#用列的平均值填充na's:
all_data = all_data.fillna(all_data.mean())
- 1
- 2
#为sklearn创建矩阵:
X_train = all_data[:train.shape[0]]
X_test = all_data[train.shape[0]:]
y = train.SalePrice
- 1
- 2
- 3
- 4
- 5
模型
现在我们将使用SciKit学习模块中的正则化线性回归模型。我将尝试l_1(套索)和l_2(岭)的正规化。我还将定义一个返回交叉验证RMSE错误的函数,这样我们就可以评估模型并选择最佳的调优参数。
from sklearn.linear_model import Ridge, RidgeCV, ElasticNet, LassoCV, LassoLarsCV
from sklearn.model_selection import cross_val_score
def rmse_cv(model): rmse= np.sqrt(-cross_val_score(model, X_train, y, scoring="neg_mean_squared_error", cv = 5)) return(rmse)
- 1
- 2
- 3
- 4
- 5
- 6
model_ridge = Ridge()
- 1
岭模型的主要调整参数是alpha——一个测量模型灵活性的正则化参数。正则化程度越高,模型越不容易过度拟合。但是,它也会失去灵活性,可能无法捕获数据中的所有信号。
alphas = [0.05, 0.1, 0.3, 1, 3, 5, 10, 15, 30, 50, 75]
cv_ridge = [rmse_cv(Ridge(alpha = alpha)).mean() for alpha in alphas]
- 1
- 2
- 3
cv_ridge = pd.Series(cv_ridge, index = alphas)
cv_ridge.plot(title = "Validation - Just Do It")
plt.xlabel("alpha")
plt.ylabel("rmse")
- 1
- 2
- 3
- 4
Text(0,0.5,'rmse')
- 1
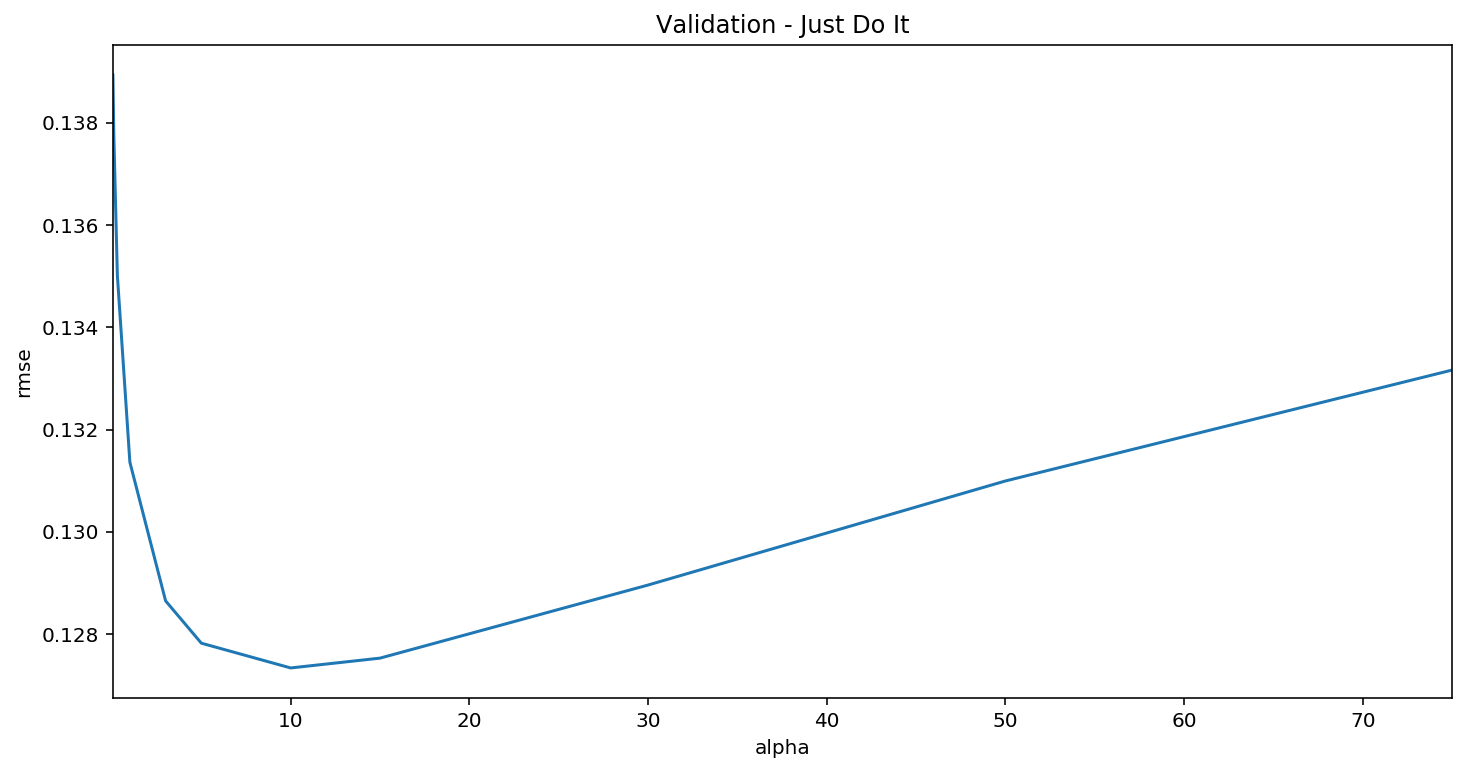
注意上面的U形曲线。当alpha太大时,正则化太强,模型无法捕获数据中的所有复杂性。然而,如果我们让模型过于灵活(alpha小),模型就会开始过度拟合。根据上面的图,alpha=10的值大约是右的。
cv_ridge.min()
- 1
0.1273373466867077
- 1
所以对于岭回归,我们得到了大约0.127的rmsle。
让我们试试套索模型。我们将在这里做一个稍微不同的方法,并使用内置的lasso cv为我们找出最好的alpha。出于某种原因,拉索cv中的alphas实际上是反向的,或者脊中的alphas。
model_lasso = LassoCV(alphas = [1, 0.1, 0.001, 0.0005]).fit(X_train, y)
- 1
rmse_cv(model_lasso).mean()
- 1
0.12314421090977452
- 1
好极了!套索的性能更好,所以我们只需要用这个来预测测试集。关于套索的另一个好处是它为你做了特征选择——设置了它认为不重要的特征系数为零。让我们来看看系数:
coef = pd.Series(model_lasso.coef_, index = X_train.columns)
- 1
print("Lasso picked " + str(sum(coef != 0)) + " variables and eliminated the other " + str(sum(coef == 0)) + " variables")
- 1
Lasso picked 110 variables and eliminated the other 178 variables
- 1
做得好套索。然而,这里需要注意的一点是,所选的特性不一定是“正确的”特性,特别是因为在这个数据集中有很多共线特性。在这里尝试的一个想法是在增强的样本上运行lasso几次,看看特性选择有多稳定。
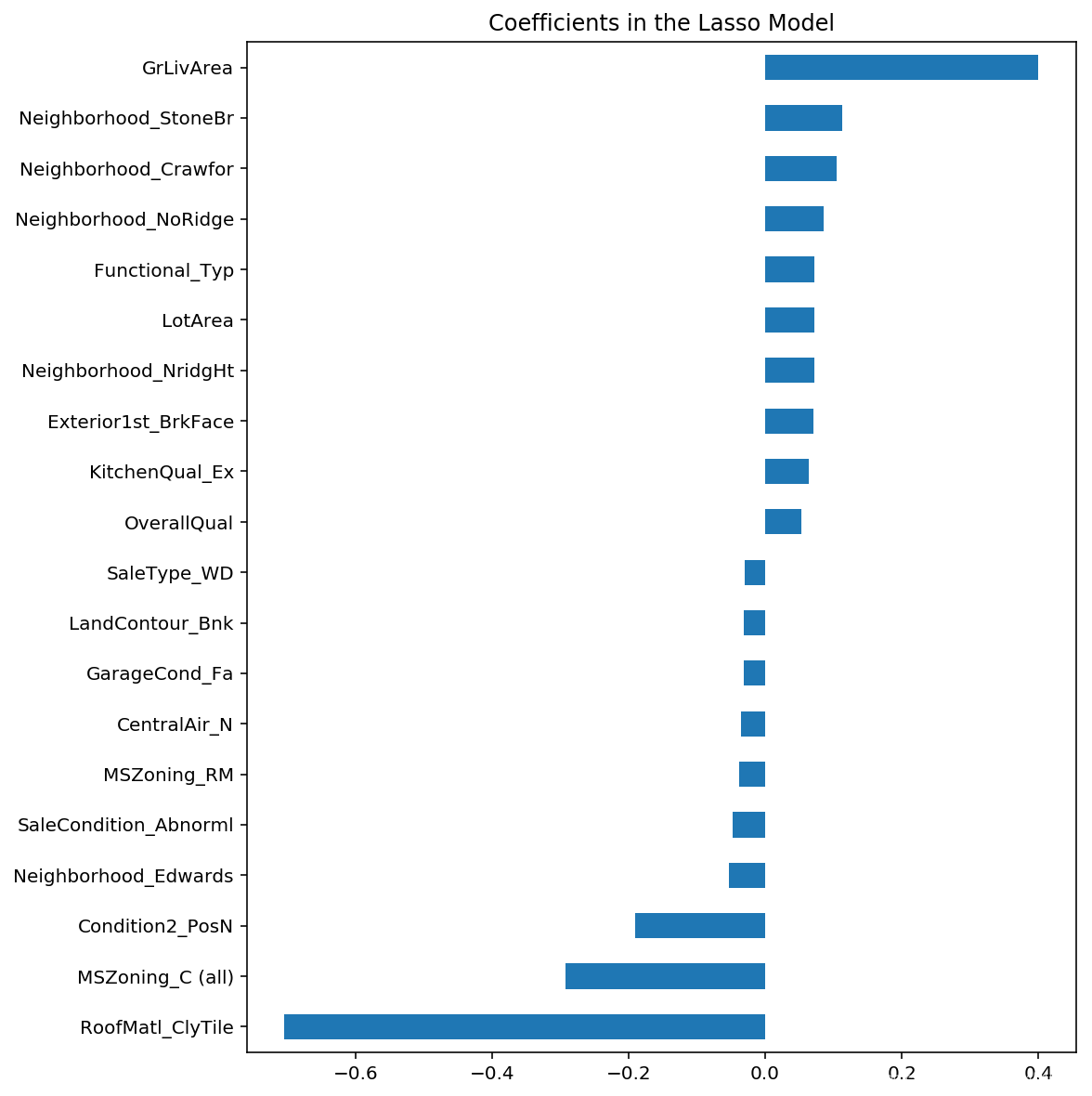
我们还可以直接看看最重要的系数是什么:
imp_coef = pd.concat([coef.sort_values().head(10), coef.sort_values().tail(10)])
- 1
- 2
matplotlib.rcParams['figure.figsize'] = (8.0, 10.0)
imp_coef.plot(kind = "barh")
plt.title("Coefficients in the Lasso Model")
- 1
- 2
- 3
Text(0.5,1,'Coefficients in the Lasso Model')
- 1
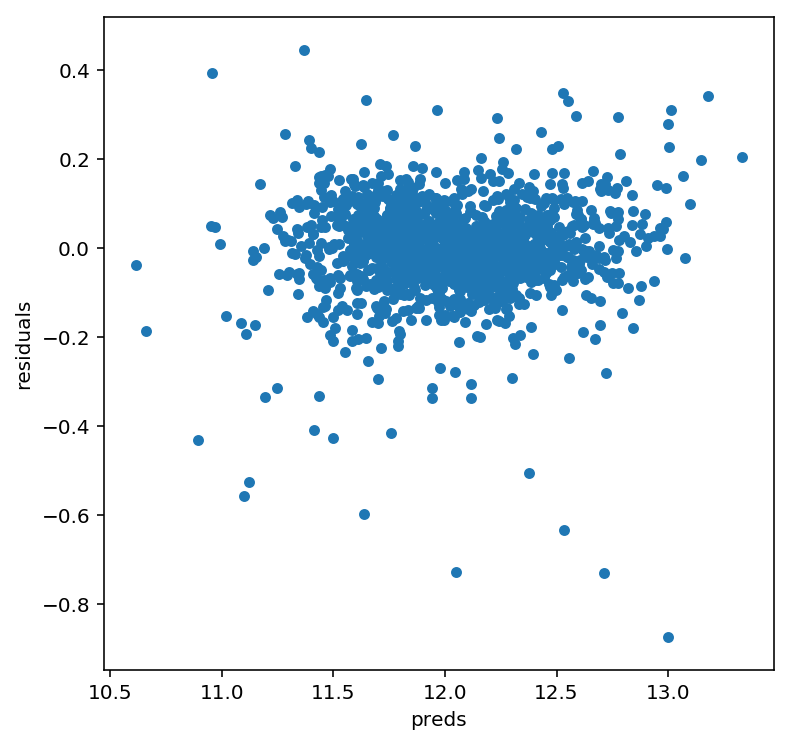
#let's look at the residuals as well:
matplotlib.rcParams['figure.figsize'] = (6.0, 6.0)
preds = pd.DataFrame({"preds":model_lasso.predict(X_train), "true":y})
preds["residuals"] = preds["true"] - preds["preds"]
preds.plot(x = "preds", y = "residuals",kind = "scatter")
- 1
- 2
- 3
- 4
- 5
- 6
<matplotlib.axes._subplots.AxesSubplot at 0x26801c06780>
- 1
文章来源: maoli.blog.csdn.net,作者:刘润森!,版权归原作者所有,如需转载,请联系作者。
原文链接:maoli.blog.csdn.net/article/details/89441530
- 点赞
- 收藏
- 关注作者


评论(0)