PCA方法及其应用

来源

https://www.icourse163.org/course/BIT-1001872001

主成分分析（PCA）

• 主成分分析（Principal Component Analysis，PCA）是最常用的 一种降维方法，通常用于高维数据集的探索与可视化，还可以用作数 据压缩和预处理等。
• PCA可以把具有相关性的高维变量合成为线性无关的低维变量，称为 主成分。主成分能够尽可能保留原始数据的信息。

在介绍PCA的原理之前涉及到的相关术语：

• 方差
• 协方差
• 协方差矩阵
• 特征向量和特征值

方差：是各个样本和样本均值的差的平方和的均值，用来度量一组 数据的分散程度

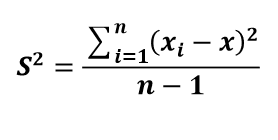
协方差：用于度量两个变量之间的线性相关性程度，若两个变量的 协方差为0，则可认为二者线性无关。协方差矩阵则是由变量的协方差值 构成的矩阵（对称阵）。

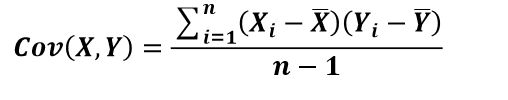
特征向量：矩阵的特征向量是描述数据集结构的非零向量，并满足 如下公式：

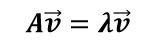
A是方阵， ?是特征向量，?

文章来源: maoli.blog.csdn.net，作者：刘润森！，版权归原作者所有，如需转载，请联系作者。

原文链接：maoli.blog.csdn.net/article/details/90581390