红黑树

什么是平衡二叉查找树

平衡二叉树（Balanced Binary Tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

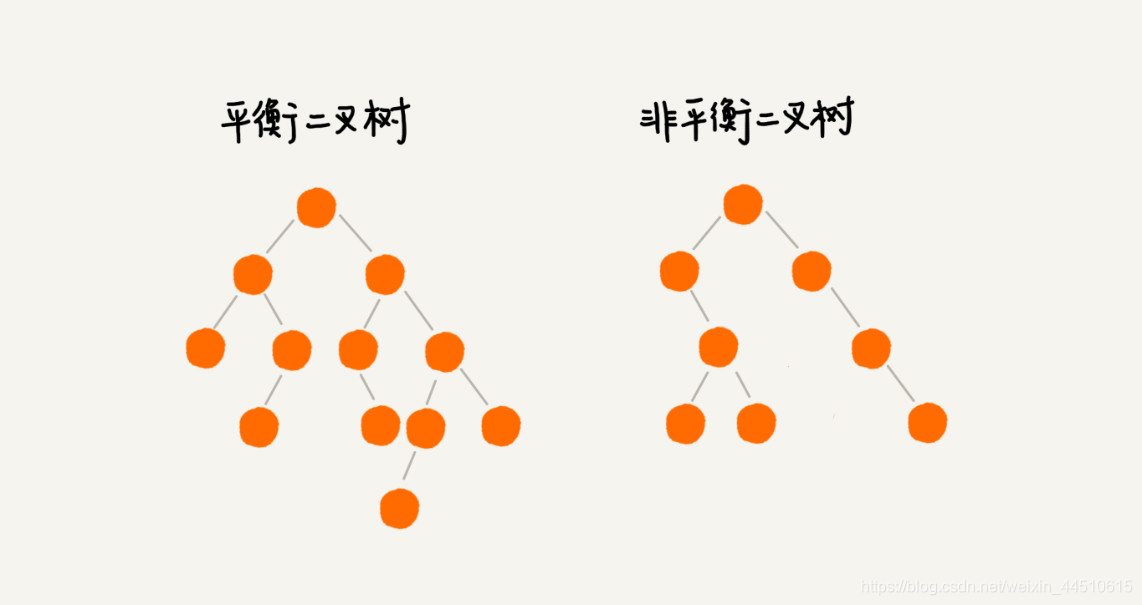
红黑树（Red Black Tree） 是一种自平衡二叉查找树

• 每个节点要么是红色，要么是黑色。
• 根节点必须是黑色
• 红色节点不能连续（也即是，红色节点的孩子和父亲都不能是红色）。红色节点是黑色节点隔开的
• 对于每个节点，从该点至null（树尾端）的任何路径，都含有相同个数的黑色节点。
• 每个叶子节点都是黑色的空节点（NIL），也就是叶子节点不存储数据

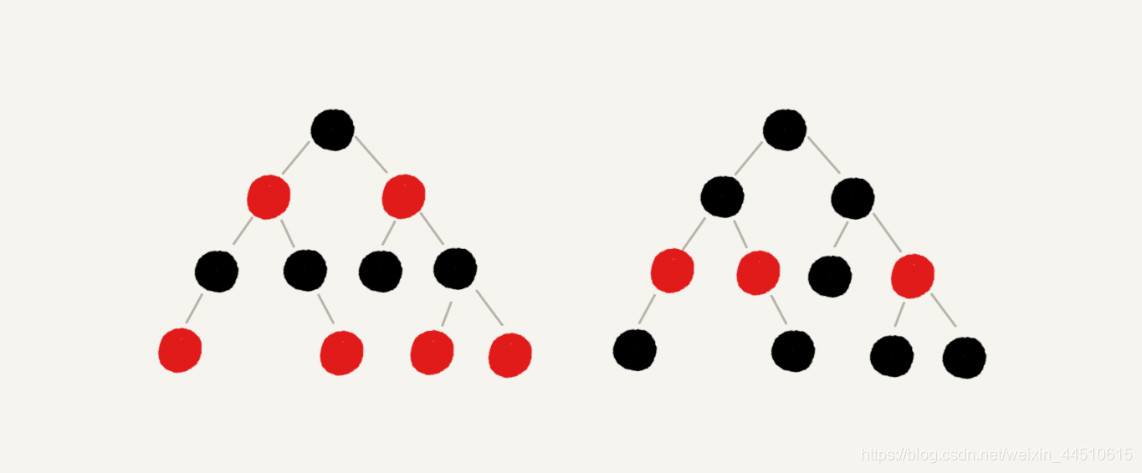
如果将红黑树的红色节点去掉，单纯包含黑色节点的红黑树的高度将发生改变

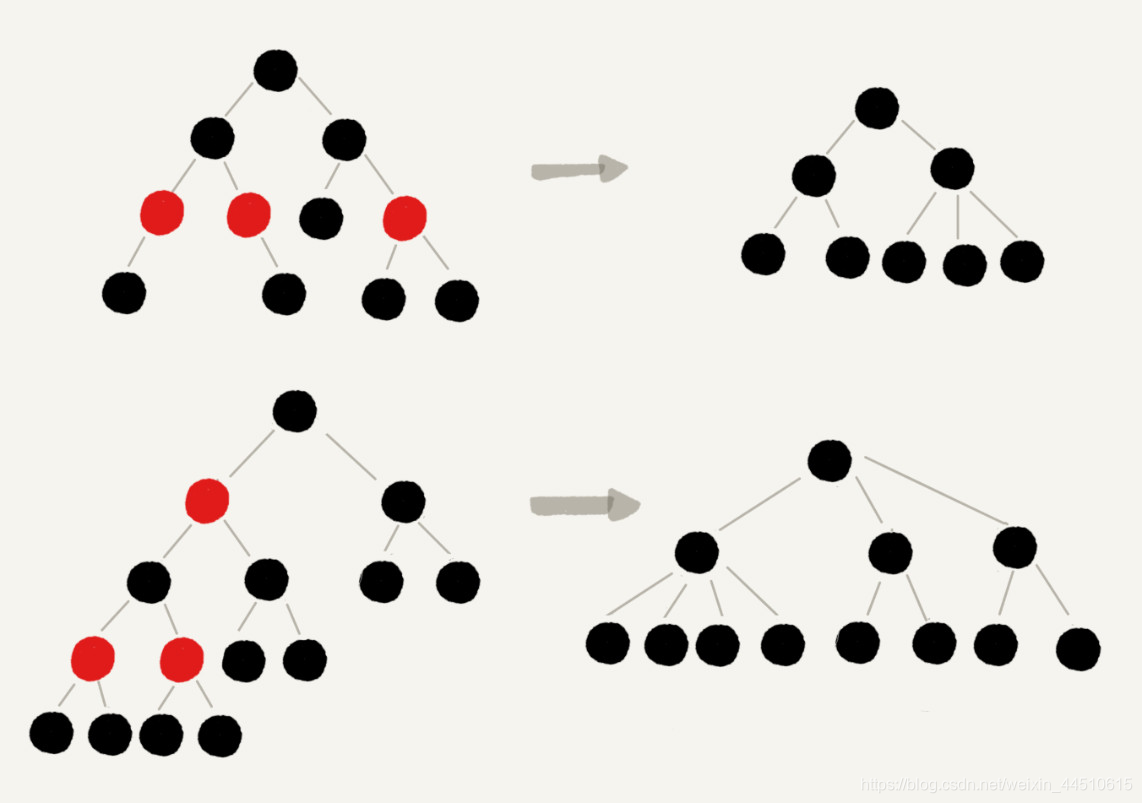
一棵极其平衡的二叉树（满二叉树或完全二叉树）的高度大约是$lo{g}_{2}n$,红黑树的高度也比较稳定趋向$lo{g}_{2}n$

红黑树两个重要操作

左旋和右旋

图中a,b,r表示子树

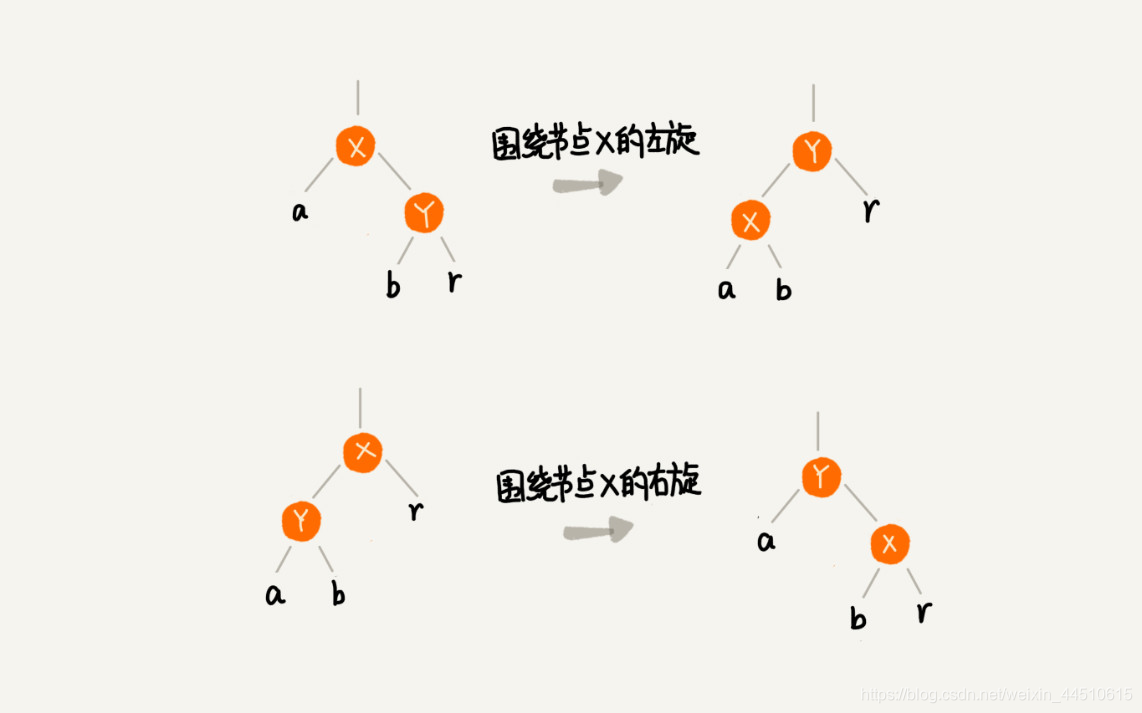
红黑树的插入

插入的节点必须是红色的，插入的节点都是放在叶子节点

• 如果插入节点的父节点是黑色的，那么什么也不用做
• 如果插入的节点是根节点，那直接改变他的颜色，把它变成黑色就可以了

关于红黑树的插入，个人理解不深

推荐大神博客
https://blog.csdn.net/abcdef314159/article/details/77193888

文章来源: maoli.blog.csdn.net，作者：刘润森！，版权归原作者所有，如需转载，请联系作者。

原文链接：maoli.blog.csdn.net/article/details/90648770