贪心科技机器学习训练营(六)
先把来源写上
来源:贪心学院,https://www.zhihu.com/people/tan-xin-xue-yuan/activities
对于这个Titanic泰坦尼克号生存绝对有笔记
通过Logistic Regression预测Titanic乘客是否能在事故中生还
1. 导入工具库和数据
import numpy as np
import pandas as pd
from sklearn import preprocessing
import matplotlib.pyplot as plt
plt.rc("font", size=14)
import seaborn as sns
sns.set(style="white") #设置seaborn画图的背景为白色
sns.set(style="whitegrid", color_codes=True)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
# 将数据读入 DataFrame
df = pd.read_csv("./titanic_data.csv")
# 预览数据
df.head()
- 1
- 2
- 3
- 4
- 5
| pclass | survived | name | sex | age | sibsp | parch | ticket | fare | cabin | embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.0 | 1.0 | Allen, Miss. Elisabeth Walton | female | 29.0000 | 0.0 | 0.0 | 24160 | 211.3375 | B5 | S |
| 1 | 1.0 | 1.0 | Allison, Master. Hudson Trevor | male | 0.9167 | 1.0 | 2.0 | 113781 | 151.5500 | C22 C26 | S |
| 2 | 1.0 | 0.0 | Allison, Miss. Helen Loraine | female | 2.0000 | 1.0 | 2.0 | 113781 | 151.5500 | C22 C26 | S |
| 3 | 1.0 | 0.0 | Allison, Mr. Hudson Joshua Creighton | male | 30.0000 | 1.0 | 2.0 | 113781 | 151.5500 | C22 C26 | S |
| 4 | 1.0 | 0.0 | Allison, Mrs. Hudson J C (Bessie Waldo Daniels) | female | 25.0000 | 1.0 | 2.0 | 113781 | 151.5500 | C22 C26 | S |
print('数据集包含的数据个数 {}.'.format(df.shape[0]))
- 1
数据集包含的数据个数 1310.
- 1
2. 查看缺失数据
# 查看数据集中各个特征缺失的情况
df.isnull().sum()
- 1
- 2
pclass 1
survived 1
name 1
sex 1
age 264
sibsp 1
parch 1
ticket 1
fare 2
cabin 1015
embarked 3
dtype: int64
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
2.1. 年龄
# "age" 缺失的百分比
print('"age" 缺失的百分比 %.2f%%' %((df['age'].isnull().sum()/df.shape[0])*100))
- 1
- 2
"age" 缺失的百分比 20.15%
- 1
约 20% 的乘客的年龄缺失了. 看一看年龄的分别情况.
ax = df["age"].hist(bins=15, color='teal', alpha=0.6)
ax.set(xlabel='age')
plt.xlim(-10,85)
plt.show()
- 1
- 2
- 3
- 4
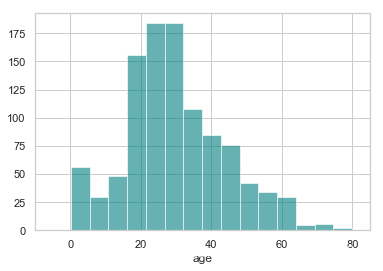
由于“年龄”的偏度不为0, 使用均值替代缺失值不是最佳选择, 这里可以选择使用中间值替代缺失值
注: 在概率论和统计学中,偏度衡量实数随机变量概率分布的不对称性。偏度的值可以为正,可以为负或者甚至是无法定义。在数量上,偏度为负(负偏态)就意味着在概率密度函数左侧的尾部比右侧的长,绝大多数的值(不一定包括中位数在内)位于平均值的右侧。偏度为正(正偏态)就意味着在概率密度函数右侧的尾部比左侧的长,绝大多数的值(不一定包括中位数)位于平均值的左侧。偏度为零就表示数值相对均匀地分布在平均值的两侧,但不一定意味着其为对称分布。
# 年龄的均值
print('The mean of "Age" is %.2f' %(df["age"].mean(skipna=True)))
# 年龄的中间值
print('The median of "Age" is %.2f' %(df["age"].median(skipna=True)))
- 1
- 2
- 3
- 4
The mean of "Age" is 29.88
The median of "Age" is 28.00
- 1
- 2
2.2. 仓位
# 仓位缺失的百分比
print('"Cabin" 缺失的百分比 %.2f%%' %((df['cabin'].isnull().sum()/df.shape[0])*100))
- 1
- 2
"Cabin" 缺失的百分比 77.48%
- 1
约 77% 的乘客的仓位都是缺失的, 最佳的选择是不使用这个特征的值.
2.3. 登船地点
# 登船地点的缺失率
print('"Embarked" 缺失的百分比 %.2f%%' %((df['embarked'].isnull().sum()/df.shape[0])*100))
- 1
- 2
"Embarked" 缺失的百分比 0.23%
- 1
只有 0.23% 的乘客的登船地点数据缺失, 可以使用众数替代缺失的值.
print('按照登船地点分组 (C = Cherbourg, Q = Queenstown, S = Southampton):')
print(df['embarked'].value_counts())
sns.countplot(x='embarked', data=df, palette='Set2')
plt.show()
- 1
- 2
- 3
- 4
按照登船地点分组 (C = Cherbourg, Q = Queenstown, S = Southampton):
S 914
C 270
Q 123
Name: embarked, dtype: int64
- 1
- 2
- 3
- 4
- 5
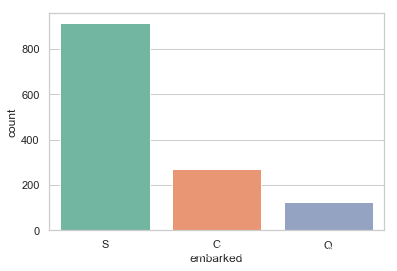
print('乘客登船地点的众数为 %s.' %df['embarked'].value_counts().idxmax())
- 1
乘客登船地点的众数为 S.
- 1
由于大多数人是在南安普顿(Southhampton)登船, 可以使用“S”替代缺失的数据值
2.4. 根据缺失数据情况调整数据
基于以上分析, 我们进行如下调整:
- 如果一条数据的 “Age” 缺失, 使用年龄的中位数 28 替代.
- 如果一条数据的 “Embarked” 缺失, 使用登船地点的众数 “S” 替代.
- 由于太多乘客的 “Cabin” 数据缺失, 从所有数据中丢弃这个特征的值.
data = df.copy()
data["age"].fillna(df["age"].median(skipna=True), inplace=True)
data["embarked"].fillna(df['embarked'].value_counts().idxmax(), inplace=True)
data.drop('cabin', axis=1, inplace=True)
- 1
- 2
- 3
- 4
# 确认数据是否还包含缺失数据
data.isnull().sum()
- 1
- 2
pclass 1
survived 1
name 1
sex 1
age 0
sibsp 1
parch 1
ticket 1
fare 2
embarked 0
dtype: int64
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
#处理仍然存在缺失数据的情况
final.dropna(inplace=True)
- 1
- 2
# 预览调整过的数据
data.head()
- 1
- 2
| pclass | survived | name | sex | age | sibsp | parch | ticket | fare | embarked | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.0 | 1.0 | Allen, Miss. Elisabeth Walton | female | 29.0000 | 0.0 | 0.0 | 24160 | 211.3375 | S |
| 1 | 1.0 | 1.0 | Allison, Master. Hudson Trevor | male | 0.9167 | 1.0 | 2.0 | 113781 | 151.5500 | S |
| 2 | 1.0 | 0.0 | Allison, Miss. Helen Loraine | female | 2.0000 | 1.0 | 2.0 | 113781 | 151.5500 | S |
| 3 | 1.0 | 0.0 | Allison, Mr. Hudson Joshua Creighton | male | 30.0000 | 1.0 | 2.0 | 113781 | 151.5500 | S |
| 4 | 1.0 | 0.0 | Allison, Mrs. Hudson J C (Bessie Waldo Daniels) | female | 25.0000 | 1.0 | 2.0 | 113781 | 151.5500 | S |
查看年龄在调整前后的分布
plt.figure(figsize=(15,8))
ax = df["age"].hist(bins=15, normed=True, stacked=True, color='teal', alpha=0.6)
df["age"].plot(kind='density', color='teal')
ax = data["age"].hist(bins=15, normed=True, stacked=True, color='orange', alpha=0.5)
data["age"].plot(kind='density', color='orange')
ax.legend(['Raw Age', 'Adjusted Age'])
ax.set(xlabel='Age')
plt.xlim(-10,85)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
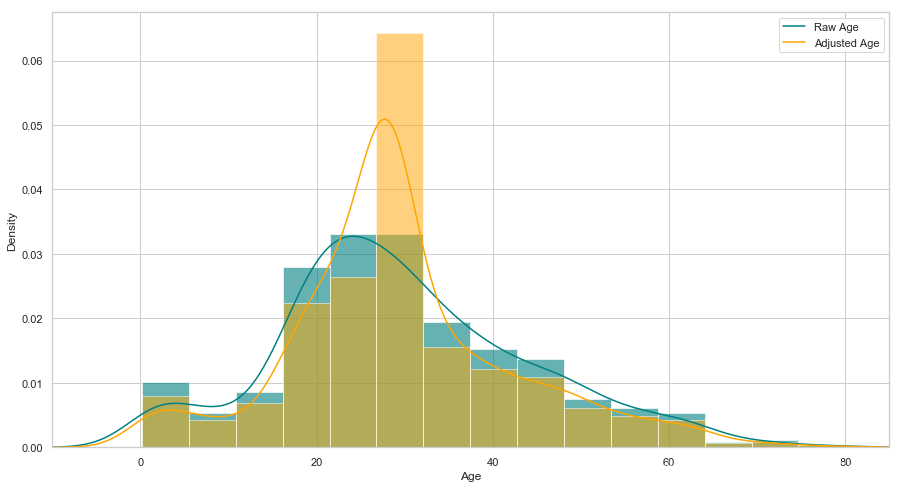
[
2.4.1. 其它特征的处理
数据中的两个特征 “sibsp” (一同登船的兄弟姐妹或者配偶数量)与“parch”(一同登船的父母或子女数量)都是代表是否有同伴同行. 为了预防这两个特征具有多重共线性, 我们可以将这两个变量转为一个变量 “TravelAlone” (是否独自一人成行)
注: 多重共线性(multicollinearity)是指多变量线性回归中,变量之间由于存在高度相关关系而使回归估计不准确。比如虚拟变量陷阱(英语:Dummy variable trap)即有可能触发多重共线性问题。
## 创建一个新的变量'TravelAlone'记录是否独自成行, 丢弃“sibsp” (一同登船的兄弟姐妹或者配偶数量)与“parch”(一同登船的父母或子女数量)
data['TravelAlone']=np.where((data["sibsp"]+data["parch"])>0, 0, 1)
data.drop('sibsp', axis=1, inplace=True)
data.drop('parch', axis=1, inplace=True)
- 1
- 2
- 3
- 4
对类别变量(categorical variables)使用独热编码(One-Hot Encoding), 将字符串类别转换为数值
# 对 Embarked","Sex"进行独热编码, 丢弃 'name', 'ticket'
final =pd.get_dummies(data, columns=["embarked","sex"])
final.drop('name', axis=1, inplace=True)
final.drop('ticket', axis=1, inplace=True)
final.head()
- 1
- 2
- 3
- 4
- 5
- 6
| pclass | survived | age | fare | TravelAlone | embarked_C | embarked_Q | embarked_S | sex_female | sex_male | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.0 | 1.0 | 29.0000 | 211.3375 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1.0 | 1.0 | 0.9167 | 151.5500 | 0 | 0 | 0 | 1 | 0 | 1 |
| 2 | 1.0 | 0.0 | 2.0000 | 151.5500 | 0 | 0 | 0 | 1 | 1 | 0 |
| 3 | 1.0 | 0.0 | 30.0000 | 151.5500 | 0 | 0 | 0 | 1 | 0 | 1 |
| 4 | 1.0 | 0.0 | 25.0000 | 151.5500 | 0 | 0 | 0 | 1 | 1 | 0 |
3. 数据分析
3.1. 年龄
plt.figure(figsize=(15,8))
ax = sns.kdeplot(final["age"][final.survived == 1], color="darkturquoise", shade=True)
sns.kdeplot(final["age"][final.survived == 0], color="lightcoral", shade=True)
plt.legend(['Survived', 'Died'])
plt.title('Density Plot of Age for Surviving Population and Deceased Population')
ax.set(xlabel='Age')
plt.xlim(-10,85)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
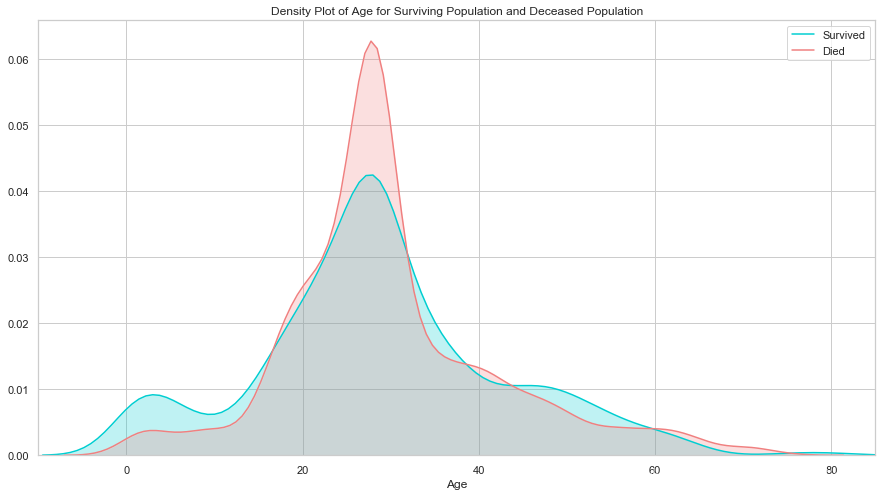
生还与遇难群体的分布相似, 唯一大的区别是生还群体中用一部分低年龄的乘客. 说明当时的人预先保留了孩子的生还机会.
3.2. 票价
plt.figure(figsize=(15,8))
ax = sns.kdeplot(final["fare"][final.survived == 1], color="darkturquoise", shade=True)
sns.kdeplot(final["fare"][final.survived == 0], color="lightcoral", shade=True)
plt.legend(['Survived', 'Died'])
plt.title('Density Plot of Fare for Surviving Population and Deceased Population')
ax.set(xlabel='Fare')
plt.xlim(-20,200)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
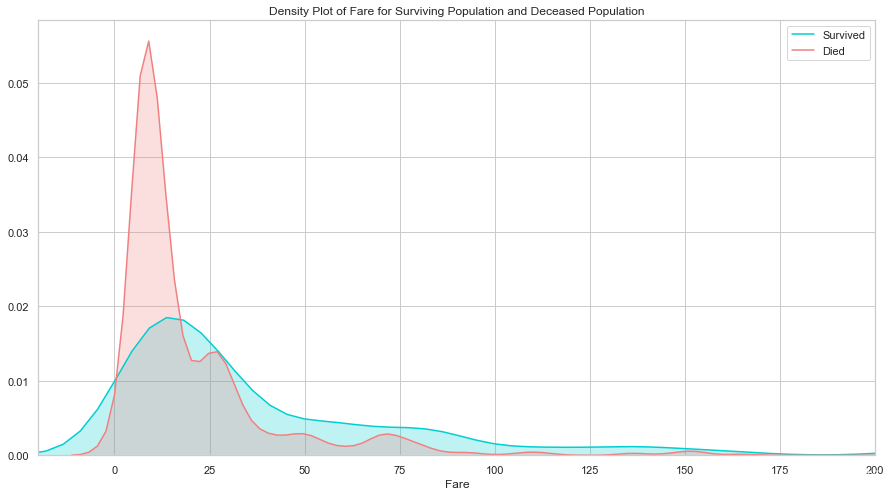
生还与遇难群体的票价分布差异比较大, 说明这个特征对预测乘客是否生还非常重要. 票价和仓位相关, 也许是仓位影响了逃生的效果, 我们接下来看仓位的分析.
3.3. 仓位
sns.barplot('pclass', 'survived', data=df, color="darkturquoise")
plt.show()
- 1
- 2
[外链图片转存失败(img-TbqcHxmW-1562946634662)(output_43_0.png)]
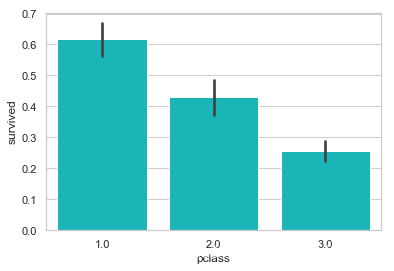
如我们所料, 一等舱的乘客生还几率最高.
3.4. 登船地点
sns.barplot('embarked', 'survived', data=df, color="teal")
plt.show()
- 1
- 2
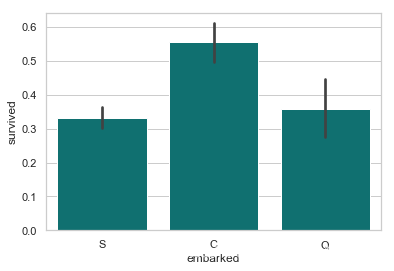
从法国 Cherbourge 登录的乘客生还率最高
3.5. 是否独自成行
sns.barplot('TravelAlone', 'survived', data=final, color="mediumturquoise")
plt.show()
- 1
- 2
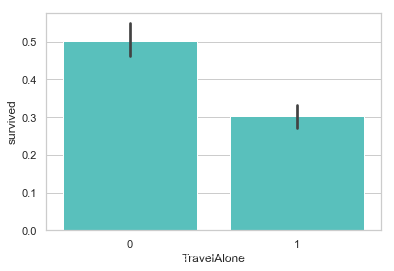
独自成行的乘客生还率比较低. 当时的年代, 大多数独自成行的乘客为男性居多.
3.6. 性别
sns.barplot('sex', 'survived', data=df, color="aquamarine")
plt.show()
- 1
- 2
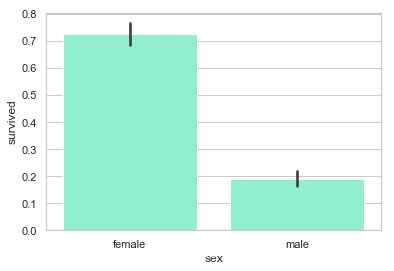
很明显, 女性的生还率比较高
4. 使用Logistic Regression做预测
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 使用如下特征做预测
cols = ["age","fare","TravelAlone","pclass","embarked_C","embarked_S","sex_male"]
# 创建 X (特征) 和 y (类别标签)
X = final[cols]
y = final['survived']
# 将 X 和 y 分为两个部分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=2) # 训练模型,
model = LogisticRegression()
model.fit(X_train,y_train.values.reshape(-1,1))
# 根据模型, 以 X_test 为输入, 生成变量 y_pred
print('Train/Test split results:')
y_pred = model.predict(X_test)
print("准确率为 %2.3f" % accuracy_score(y_test, y_pred))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
Train/Test split results:
准确率为 0.817
- 1
- 2
文章来源: maoli.blog.csdn.net,作者:刘润森!,版权归原作者所有,如需转载,请联系作者。
原文链接:maoli.blog.csdn.net/article/details/95679249
- 点赞
- 收藏
- 关注作者


评论(0)