r语言的逻辑回归分类
【摘要】 iris 是r语言内置的数据集
head(iris) # 与python的不同iris.head()
1
Sepal.LengthSepal.WidthPetal.LengthPetal.WidthSpecies5.1 3.5 1.4 0.2 setosa4.9 3.0 1.4 0.2 setosa4.7 3.2 1.3 0.2 setosa4.6 3.1 1.5...
iris 是r语言内置的数据集
head(iris) # 与python的不同iris.head()
- 1
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| 5.4 | 3.9 | 1.7 | 0.4 | setosa |
# 查看数据的行和列
dim(iris)
- 1
- 2
- 150
- 5
# 数据的类型
mode(iris)
- 1
- 2
‘list’
# columns的名字
names(iris)
- 1
- 2
- 'Sepal.Length'
- 'Sepal.Width'
- 'Petal.Length'
- 'Petal.Width'
- 'Species'
# r是data.frame py是pandas.Dateframe
str(iris)
- 1
- 2
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
- 1
- 2
- 3
- 4
- 5
- 6
# 查看数据集的属性
attributes(iris)
- 1
- 2
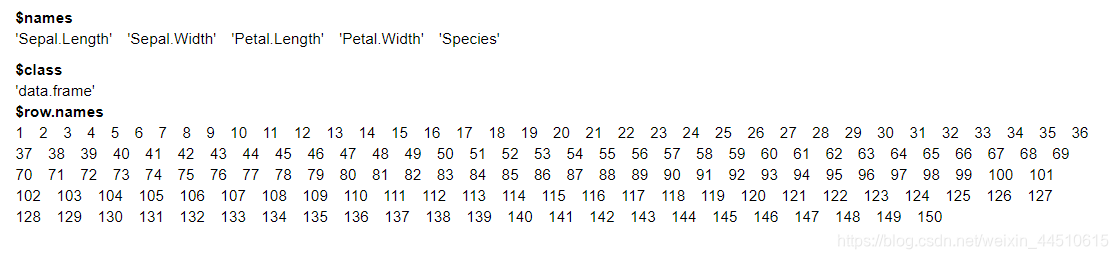
# 数据的概述
summary(iris)
- 1
- 2
Sepal.Length Sepal.Width Petal.Length Petal.Width Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 Median :5.800 Median :3.000 Median :4.350 Median :1.300 Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800 Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500 Species setosa :50 versicolor:50 virginica :50
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
# 查看分类的种类
table(iris$Species)
- 1
- 2
setosa versicolor virginica 50 50 50
- 1
- 2
# 画图 Sepal萼片长度
hist(iris$Sepal.Length)
- 1
- 2
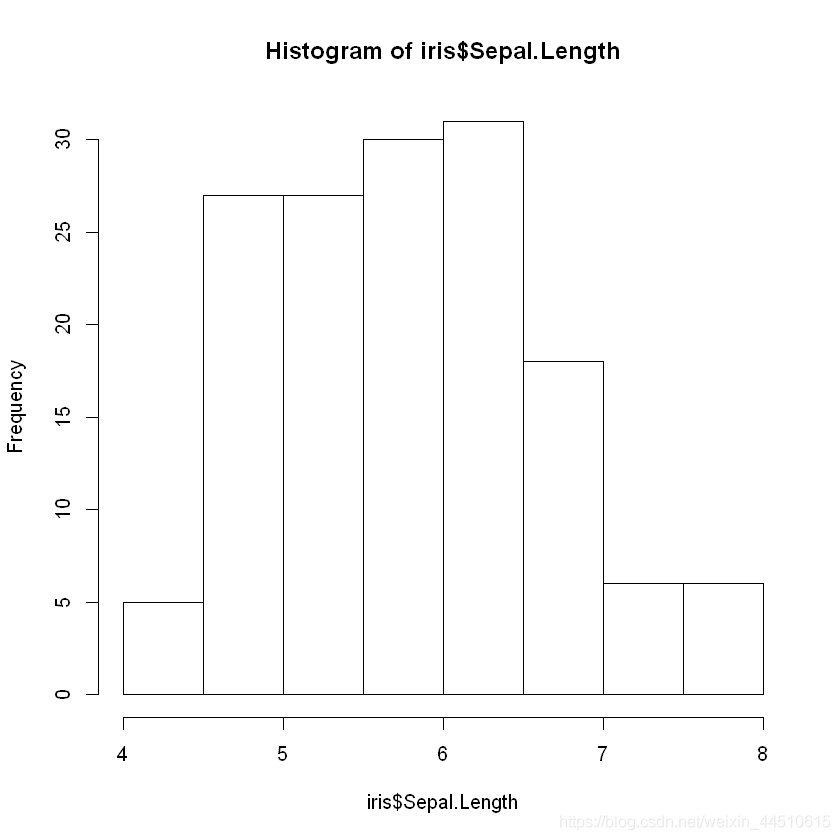
# 密度分布图
plot(density(iris$Sepal.Length))
- 1
- 2
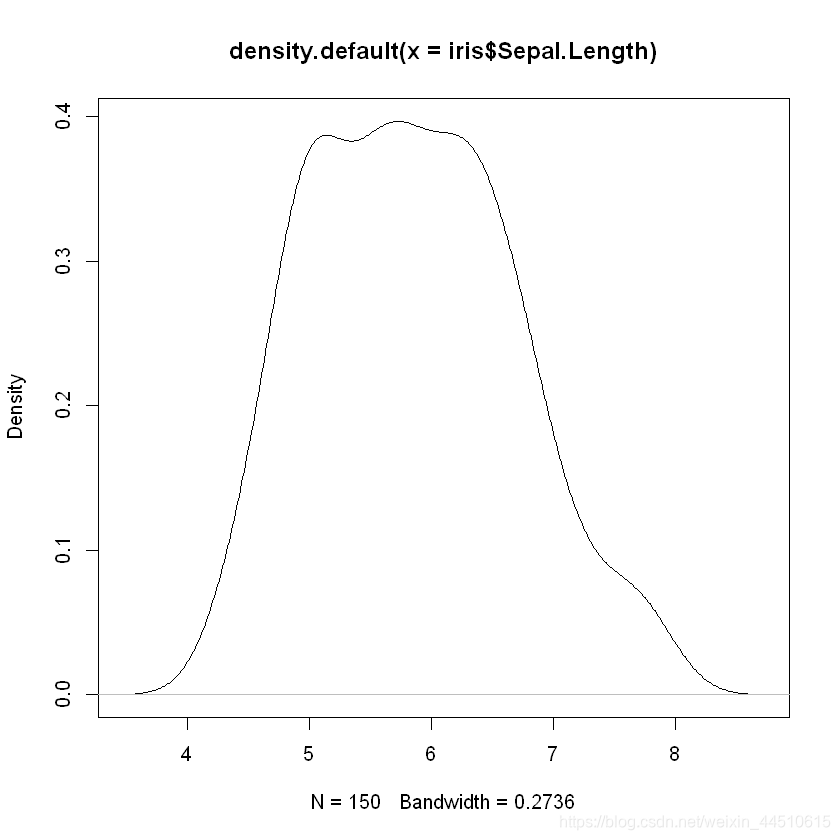
# 花萼长度散点图
plot(iris$Sepal.Length,iris$Sepal.Width)
- 1
- 2
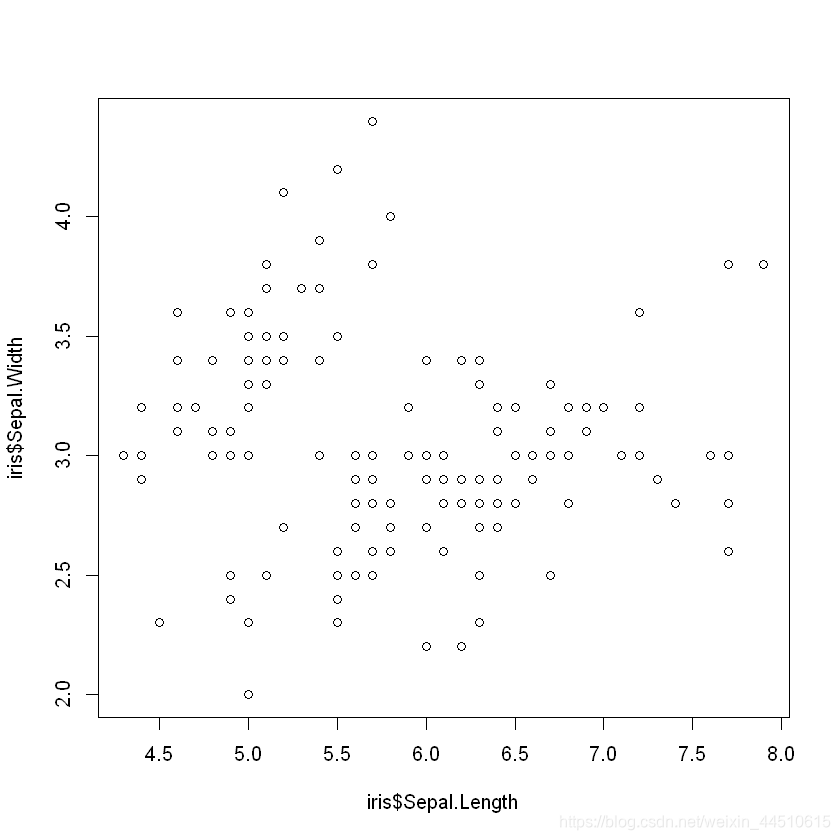
plot(iris)
- 1
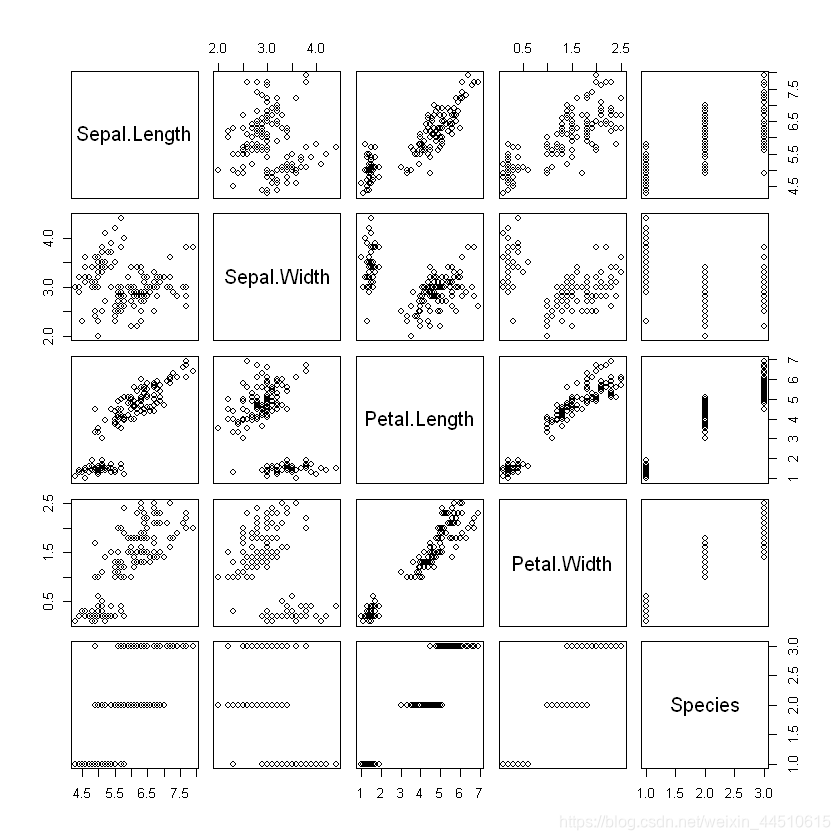
# 逻辑回归 只能分两类
a<-which(iris$Species=='virginica')
head(a) # 对应的编号
- 1
- 2
- 3
- 101
- 102
- 103
- 104
- 105
- 106
# 取出其他的两类
myir <- iris[-a,]
- 1
- 2
# 数据分样 测试和训练
s <- sample(100,80) # 100抽80
- 1
- 2
# 排序
s <- sort(s)
- 1
- 2
ir_trian <- myir[s,]
- 1
head(ir_trian)
- 1
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species | |
|---|---|---|---|---|---|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| 7 | 4.6 | 3.4 | 1.4 | 0.3 | setosa |
| 9 | 4.4 | 2.9 | 1.4 | 0.2 | setosa |
ir_test <- myir[-s,]
- 1
model <-glm(Species~.,family = binomial(link="logit"),data= ir_trian)
- 1
summary(model)
- 1
Call:
glm(formula = Species ~ ., family = binomial(link = "logit"), data = ir_trian)
Deviance Residuals: Min 1Q Median 3Q Max
-1.570e-05 -2.110e-08 2.110e-08 2.110e-08 1.865e-05 Coefficients: Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.691 681526.322 0 1
Sepal.Length -9.568 216769.252 0 1
Sepal.Width -7.254 99870.123 0 1
Petal.Length 18.946 153746.614 0 1
Petal.Width 25.341 222619.596 0 1
(Dispersion parameter for binomial family taken to be 1) Null deviance: 1.1070e+02 on 79 degrees of freedom
Residual deviance: 1.0579e-09 on 75 degrees of freedom
AIC: 10
Number of Fisher Scoring iterations: 25
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
# 残差
a<- predict(model,type="response")
- 1
- 2
# 大于0.5 为1
res_train <- ifelse(a>0.5,1,0)
- 1
- 2
b<- predict(model,type="response",newdata=ir_test)
- 1
res_test <- ifelse (b>0.5,1,0)
- 1
model <- glm(Species~.,family = binomial(link = "logit"),data= ir_trian,control= list(maxit=100))
- 1
summary(model)
- 1
Call:
glm(formula = Species ~ ., family = binomial(link = "logit"), data = ir_trian, control = list(maxit = 100))
Deviance Residuals: Min 1Q Median 3Q Max
-9.535e-06 -2.110e-08 2.110e-08 2.110e-08 1.132e-05 Coefficients: Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.292e+00 1.125e+06 0 1
Sepal.Length -1.013e+01 3.577e+05 0 1
Sepal.Width -7.501e+00 1.645e+05 0 1
Petal.Length 1.988e+01 2.534e+05 0 1
Petal.Width 2.634e+01 3.667e+05 0 1
(Dispersion parameter for binomial family taken to be 1) Null deviance: 1.1070e+02 on 79 degrees of freedom
Residual deviance: 3.8911e-10 on 75 degrees of freedom
AIC: 10
Number of Fisher Scoring iterations: 26
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
文章来源: maoli.blog.csdn.net,作者:刘润森!,版权归原作者所有,如需转载,请联系作者。
原文链接:maoli.blog.csdn.net/article/details/95904457
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)