R语言基础练习与入门实践
【摘要】
练习: 熟练使用R软件
实践1:最初几步
x=1:100#把1,2,...,100个整数向量赋值到x(x=1:100) #同上, 只不过显示出来sample(x,20) #从1,...,100中随机不放回地抽取20个值作为样本set.seed(0);sample(1:10,3)#先设随机种子再抽样.#从1,...,200000中随机不放回地抽取10000个...
练习: 熟练使用R软件
实践1:最初几步
-
x=1:100#把1,2,...,100个整数向量赋值到x
-
(x=1:100) #同上, 只不过显示出来
-
sample(x,20) #从1,...,100中随机不放回地抽取20个值作为样本
-
set.seed(0);sample(1:10,3)#先设随机种子再抽样.
-
#从1,...,200000中随机不放回地抽取10000个值作为样本:
-
z=sample(1:200000,10000)
-
z[1:10]#方括号中为向量z的下标
-
y=c(1,3,7,3,4,2)
-
z[y]#以y为下标的z的元素值
-
(z=sample(x,100,rep=T))#从x放回地抽取100个随机样本
-
(z1=unique(z))
-
length(z1)#z中不同的元素个数
-
xz=setdiff(x,z) #x和z之间的不同元素--集合差
-
sort(union(xz,z))#对xz及z的并的元素从小到大排序
-
setequal(union(xz,z),x) #对xz及z的并的元素与x是否一样
-
intersect(1:10,7:50) #两个数据的交
-
sample(1:100,20,prob=1:100)#从1:100中不等概率随机抽样,
-
#各数目抽到的概率与1:100成比例
实践2: 一些简单运算
-
pi *10^2 #能够用?”*”来看基本算术运算方法, pi是圆周率
-
"*"(pi, "^"(10,2)) #和上面一样, 有些繁琐, 是吧! 没有人这么用
-
pi * (1:10)^-2.3#可以对向量求指数幂
-
x = pi * 10^2
-
x
-
print(x) #和上面一样
-
(x=pi *10^2) #赋值带打印
-
pi^(1:5) #指数也可以是向量
-
print(x, digits = 12)#输出x的12位数字
实践3:关于R对象的类型等
-
这里写代码片x=pi*10^2
-
class(x) #x的class
-
typeof(x) #x的type
-
class(cars)#cars是一个R中自带的数据
-
typeof(cars) #cars的type
-
names(cars)#cars数据的变量名字
-
summary(cars) #cars的汇总
-
head(cars)#cars的头几行数据, 和cars[1:6,]相同
-
tail(cars) #cars的最后几行数据
-
str(cars)#也是汇总
-
row.names(cars) #行名字
-
attributes(cars)#cars的一些信息
-
class(dist~speed)#公式形式,"~"左边是因变量,右边是自变量
-
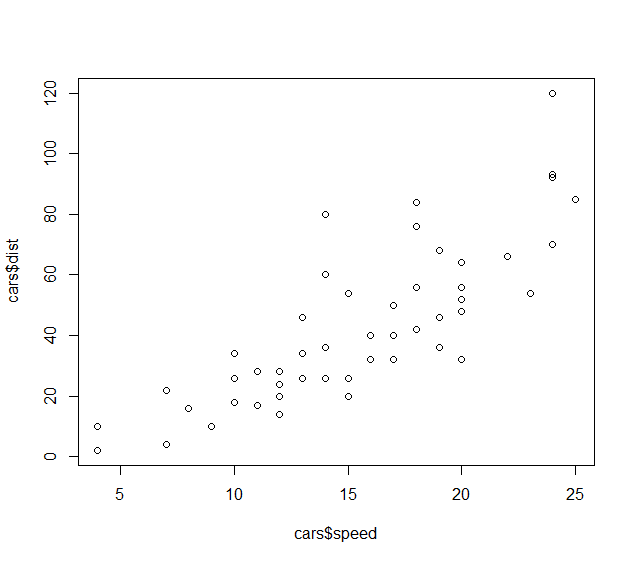
plot(dist ~speed,cars)#两个变量的散点图
-
plot(cars$speed,cars$dist) #同上
实践4: 包括简单自变量为定量变量及定性变量的回归
-
ncol(cars);nrow(cars) #cars的行列数
-
dim(cars) #cars的维数
-
lm(dist ~ speed, data = cars)#以dist为因变量,speed为自变量做OLS
-
cars$qspeed =cut(cars$speed, breaks=quantile(cars$speed),
-
include.lowest = TRUE) #增加定性变量qspeed, 四分位点为分割点
-
names(cars) #数据cars多了一个变量
-
cars[3]#第三个变量的值和cars[,3]类似
-
table(cars[3])#列表
-
is.factor(cars$qspeed)
-
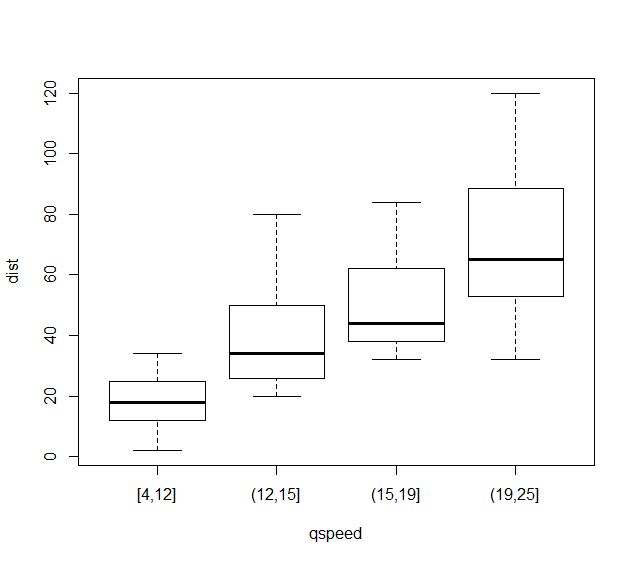
plot(dist ~ qspeed, data = cars)#点出箱线图
-
(a=lm(dist ~ qspeed, data = cars))#拟合线性模型(简单最小二乘回归)
-
summary(a)#回归结果(包括一些检验)
实践5: 简单样本描述统计量等等
-
这里写代码片x <- round(runif(20,0,20), digits=2)#四舍五入
-
summary(x) #汇总
-
min(x);max(x) #极值, 与range(x)类似
-
median(x) # 中位数(median)
-
mean(x) # 均值(mean)
-
var(x) #方差(variance)
-
sd(x) # 标准差(standard deviation),为方差的平方根
-
sqrt(var(x)) #平方根
-
rank(x) # 秩(rank)
-
order(x)#升幂排列的x的下标
-
order(x,decreasing = T)#降幂排列的x的下标
-
x[order(x)] #和sort(x)相同
-
sort(x) #同上: 升幂排列的x
-
sort(x,decreasing=T)#sort(x,dec=T) 降幂排列的x
-
sum(x);length(x)#元素和及向量元素个数
-
round(x) #四舍五入,等于round(x,0),而round(x,5)为留到小数点后5位
-
fivenum(x) # 五数汇总, quantiles
-
quantile(x) # 分位点 quantiles (different convention)有多种定义
-
quantile(x, c(0,.33,.66,1))
-
mad(x) # "median average distance":
-
cummax(x)#累积最大值
-
cummin(x)#累积最小值
-
cumprod(x)#累积积
-
cor(x,sin(x/20)) #线性相关系数 (correlation)
实践6:简单图形
-
x=rnorm(200)#200个随机正态数赋值到x
-
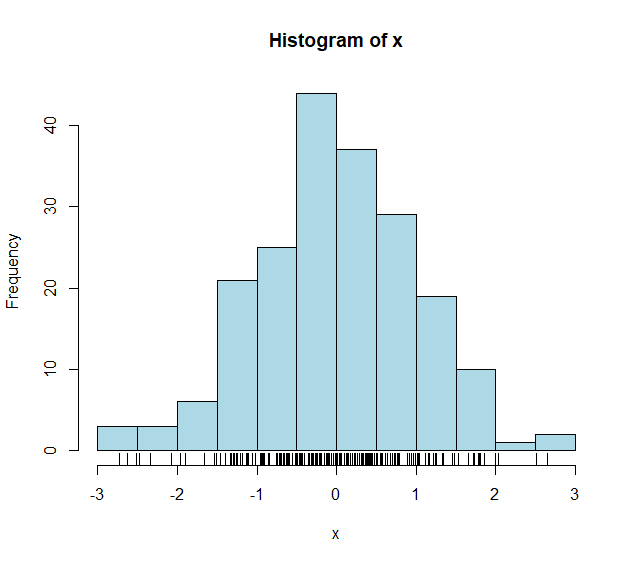
hist(x, col = "light blue")#直方图(histogram)
-
rug(x) #在直方图下面加上实际点的大小
-
stem(x)#茎叶图
-
x <- rnorm(500)
-
y <- x + rnorm(500) #构造一个线性关系
-
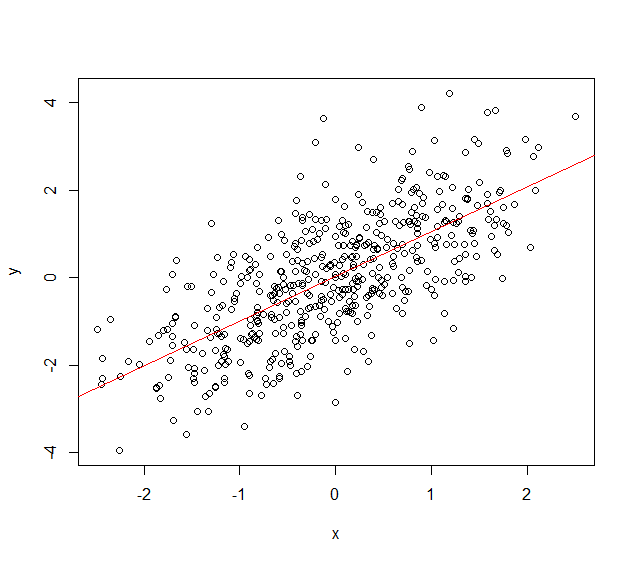
plot(y~ x) #散点图
-
a=lm(y~x) #做回归
-
abline(a,col="red")#或者abline(lm(y~x),col="red")散点图加拟合线
-
print("Hello World!")
-
paste("x 的最小值= ", min(x)) #打印
-
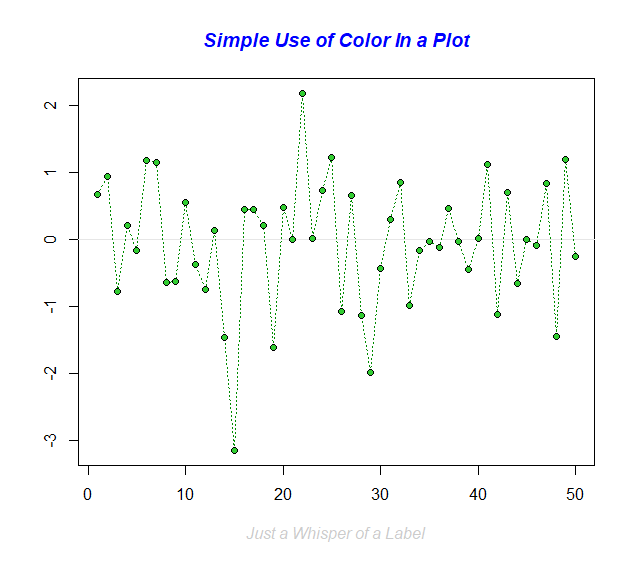
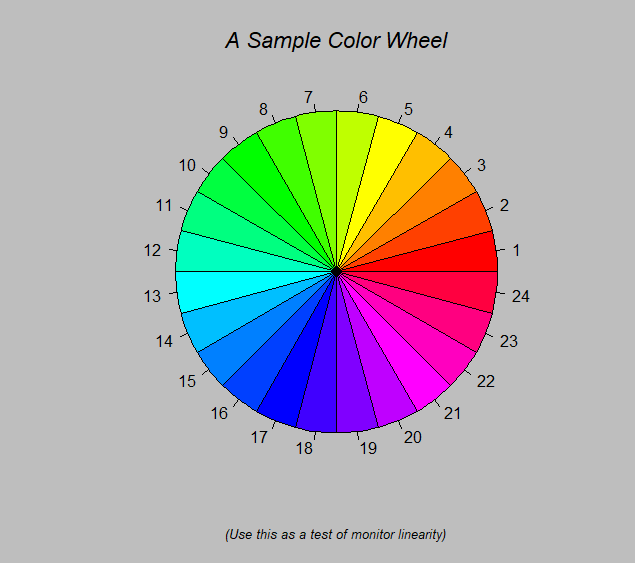
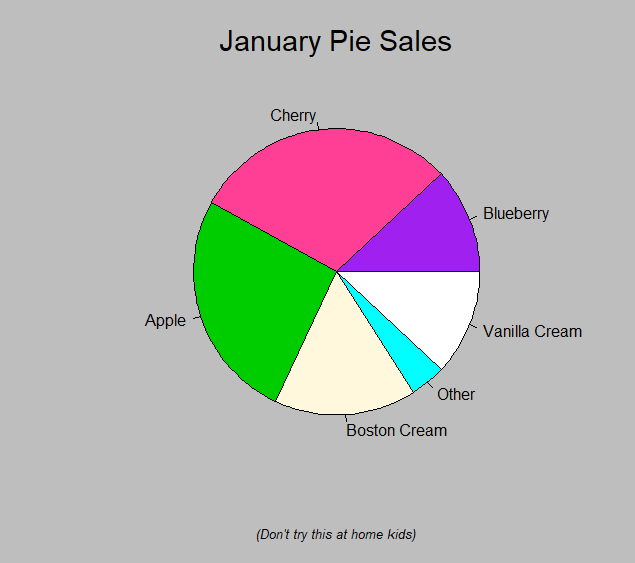
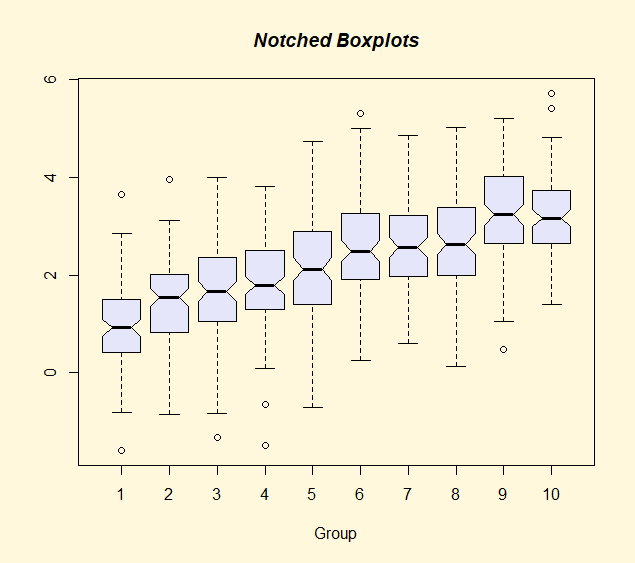
demo(graphics)#演示画图(点Enter来切换)
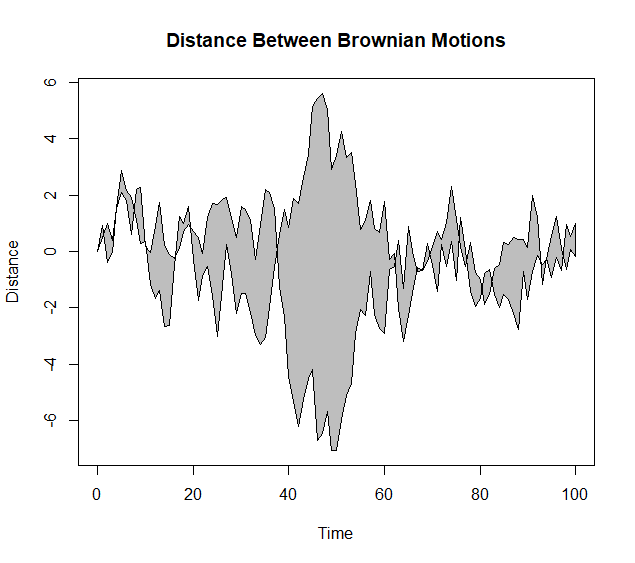
实践7: 复数运算和求函数极值
-
#(2+4i)^-3.5+(2i+4.5)*(-1.7-2.3i)/((2.6-7i)*(-4+5.1i))#复数运算
-
#下面构造一个10维复向量, 实部和虚部均为10个标准状态样本点:
-
(z <-complex(real=rnorm(10), imaginary =rnorm(10)))
-
complex(re=rnorm(3),im=rnorm(3))#3维复向量
-
Re(z) #实部
-
Im(z) #虚部
-
Mod(z) #模
-
Arg(z) #辐角
-
choose(3,2) #组合
-
factorial(6)#排列6!
-
#解方程:
-
f=function(x) x^3-2*x-1
-
uniroot(f,c(0,2))#迭代求根
-
#如果知道根为极值
-
f=function(x) x^2+2*x+1 #定义一个二次函数
-
optimize(f,c(-2,2))#在区间(-2,2)间求极值
实践8:字符型向量
-
a=factor(letters[1:10])#letters:小写字母的向量,LETTERS:大写字母
-
a[3]="w" #不行! 会给出警告
-
a=as.character(a) #转换一下
-
a[3]="w" #可以了
-
a;factor(a) #两种不同的类型
实践9:数据输入输出
-
x=scan()#从屏幕输入数据, 可以键入, 也可以粘贴,可多行输入,空行后Enter
-
1.5 2.6 3.7 2.1 8.9 12 -1.2 -4
-
-
x=c(1.5,2.6,3.7,2.1,8.9,12,-1.2,-4)#等价于上面
-
w=read.table(file.choose(),header=T)#从列表中选择有变量名的数据
-
setwd(“f:/2010stat”)#或setwd("f:\2010stat")#建立工作路径
-
(x=rnorm(20)) #给x赋值20个标准正态数据值
-
#(注:有常见分布的随机数, 分布函数,密度函数及分位数函数)
-
write(x,"f:/2010stat/test.txt")#把数据写入文件(路径要对)
-
y=scan("f:/2010stat/test.txt");y #扫描文件数值数据到y
-
y=iris;y[1:5,];str(y) #iris是R自带数据
-
write.table(y,"test.txt",row.names=F)#把数据写入文本文件
-
w=read.table("f:/2010stat/test.txt",header=T)#读带有变量名的数据
-
str(w) #汇总
-
write.csv(y,"test.csv")#把数据写入csv文件
-
v=read.csv("f:/2010stat/test.csv")#读入csv数据文件
-
str(v) #汇总
-
data=read.table("clipboard")#读入剪贴板的数据
实践10:序列等等
-
(z=seq(-1,10,length=100))#-1到10等间隔的100个数的序列
-
z=seq(-1,10,len=100)#和上面等价写法
-
(z=seq(10,-1,-0.1)) #10到-1间隔为-0.1的序列
-
(x=rep(1:3,3)) #三次重复1:3
-
(x=rep(3:5,1:3)) #自己看, 这又是什么呢?
-
x=rep(c(1,10),c(4,5))
-
w=c(1,3,x,z);w[3]#把数据(包括向量)组合(combine)成一个向量
-
x=rep(0,10);z=1:3;x+z #向量加法(如果长度不同, R如何给出警告和结果?)
-
x*z #向量乘法
-
rev(x)#颠倒次序
-
z=c("no cat","has ","nine","tails") #字符向量
-
z[1]=="no cat" #双等号为逻辑等式
-
z=1:5
-
z[7]=8;z #什么结果? 注:NA为缺失值(not available)
-
z=NULL
-
z[c(1,3,5)]=1:3;
-
z
-
rnorm(10)[c(2,5)]
-
z[-c(1,3)]#去掉第1、3元素
-
z=sample(1:100,10);z
-
which(z==max(z))#给出最大值的下标
实践11: 矩阵
-
x=sample(1:100,12);x #抽样
-
all(x>0);all(x!=0);any(x>0);(1:10)[x>0]#逻辑符号的应用
-
diff(x) #差分
-
diff(x,lag=2) #差分
-
x=matrix(1:20,4,5);x #矩阵的构造
-
x=matrix(1:20,4,5,byrow=T);x#矩阵的构造, 按行排列
-
t(x) #矩阵转置
-
x=matrix(sample(1:100,20),4,5)
-
2*x
-
x+5
-
y=matrix(sample(1:100,20),5,4)
-
x+t(y) #矩阵之间相加
-
(z=x%*%y) #矩阵乘法
-
z1=solve(z) # solve(a,b)可以解ax=b方程
-
z1%*%z #应该是单位向量, 但浮点运算不可能得到干净的0
-
round(z1%*%z,14) #四舍五入
-
b=solve(z,1:4); b #解联立方程
-
#\end{verbatim}}
实践12:矩阵继续
-
nrow(x);ncol(x);dim(x)#行列数目
-
x=matrix(rnorm(24),4,6)
-
x[c(2,1),]#第2和第1行
-
x[,c(1,3)] #第1和第3列
-
x[2,1] #第[2,1]元素
-
x[x[,1]>0,1] #第1列大于0的元素
-
sum(x[,1]>0) #第1列大于0的元素的个数
-
sum(x[,1]<=0) #第1列不大于0的元素的个数
-
x[,-c(1,3)]#没有第1、3列的x.
-
diag(x) #x的对角线元素
-
diag(1:5) #以1:5为对角线,其它元素为0的对角线矩阵
-
diag(5) #5维单位矩阵
-
x[-2,-c(1,3)]#没有第2行、第1、3列的x
-
x[x[,1]>0&x[,3]<=1,1]#第1列>0并且第3列<=1的第1列元素
-
x[x[,2]>0|x[,1]<.51,1]#第1列<.51或者第2列>0的第1列元素
-
x[!x[,2]<.51,1]#第1列中相应于第2列中>=.51的元素
-
apply(x,1,mean)#对行(第一维)求均值
-
apply(x,2,sum)#对列(第二维)求和
-
x=matrix(rnorm(24),4,6)
-
x[lower.tri(x)]=0;x #得到上三角阵,
-
#为得到下三角阵, 用x[upper.tri(x)]=0)
实践13:高维数组
-
x=array(runif(24),c(4,3,2))
-
x#从24个均匀分布的样本点构造4乘3乘2的三维数组
-
is.matrix(x)
-
dim(x)#得到维数(4,3,2)
-
is.matrix(x[1,,])#部分三维数组是矩阵
-
x=array(1:24,c(4,3,2))
-
x[c(1,3),,]
-
x=array(1:24,c(4,3,2))
-
apply(x,1,mean) #可以对部分维做运算
-
apply(x,1:2,sum) #可以对部分维做运算
-
apply(x,c(1,3),prod) #也以对部分维做运算
实践14:矩阵与向量之间的运算
-
x=matrix(1:20,5,4) #5乘4矩阵
-
sweep(x,1,1:5,"*")#把向量1:5的每个元素乘到每一行
-
sweep(x,2,1:4,"+")#把向量1:4的每个元素加到每一列
-
x*1:5
-
sweep(x,2,1:4,"+")#标准化,即每一元素减去该列均值,除以该列标准差:
-
(x=matrix(sample(1:100,24),6,4));(x1=scale(x))
-
(x2=scale(x,scale=F))#自己观察并总结结果
-
(x3=scale(x,center=F)) #自己观察并总结结果
-
round(apply(x1,2,mean),14) #自己观察并总结结果
-
apply(x1,2,sd)#自己观察并总结结果
-
round(apply(x2,2,mean),14);apply(x2,2,sd)#自己观察并总结结果
-
round(apply(x3,2,mean),14);apply(x3,2,sd)#自己观察并总结结果
实践15:缺失值, 数据的合并
-
airquality #有缺失值(NA)的R自带数据
-
complete.cases(airquality)#没有缺失值的那些行中那些是缺失的
-
which(complete.cases(airquality)==F) #没有缺失值的行号
-
sum(complete.cases(airquality)) #完整观测值的个数
-
na.omit(airquality) #删去缺失值的数据
-
#附加, 横或竖合并数据: append,cbind,rbind
-
x=1:10;x[12]=3
-
(x1=append(x,77,after=5))
-
cbind(1:5,rnorm(5))
-
rbind(1:5,rnorm(5))
-
cbind(1:3,4:6);rbind(1:3,4:6) #去掉矩阵重复的行
-
(x=rbind(1:5,runif(5),runif(5),1:5,7:11))
-
x[!duplicated(x),]
-
unique(x)
实践16: list
-
#list可以是任何对象(包括list本身)的集合
-
z=list(1:3,Tom=c(1:2,a=list("R",letters[1:5]),w="hi!"))
-
z[[1]];z[[2]]
-
z$T
-
z$T$a2
-
z$T[[3]]
-
z$T$w
实践17:条形图和表
-
x =scan()#30个顾客在五个品牌中的挑选
-
3 3 3 4 1 4 2 1 3 2 5 3 1 2 5 2 3 4 2 2 5 3 1 4 2 2 4 3 5 2
-
-
barplot(x) #错误的图
-
table(x) #制表
-
barplot(table(x)) #正确的图
-
barplot(table(x)/length(x)) #比例图(和上图形状一样)
-
table(x)/length(x)
-
#\end{verbatim}}
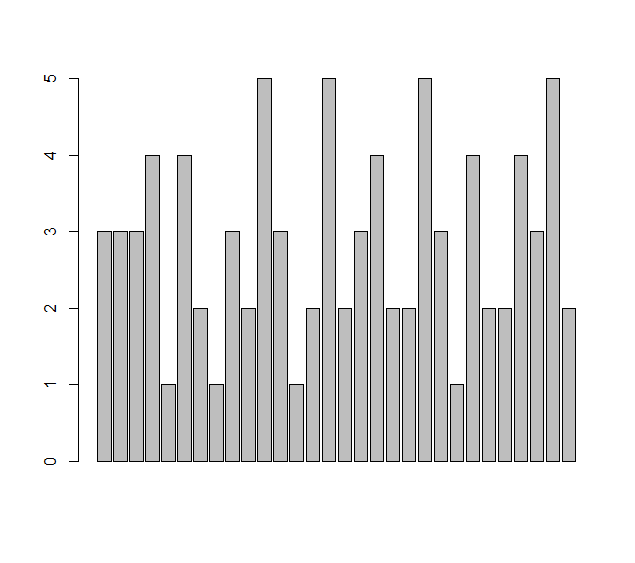
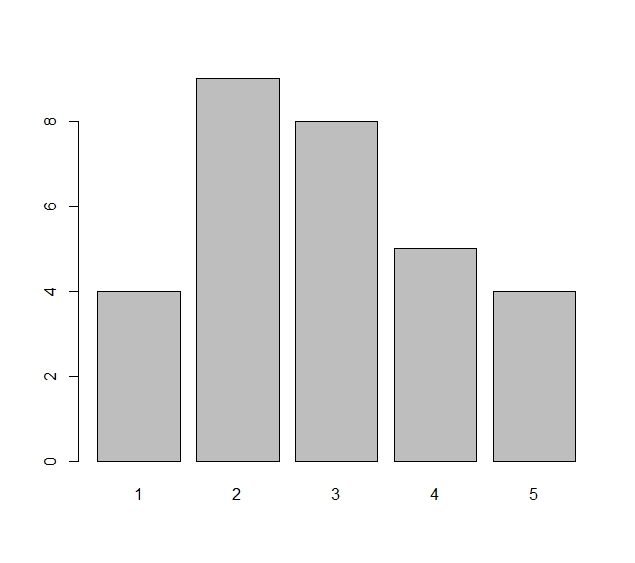
实践18: 形成表格
-
library(MASS)#载入软件包MASS
-
quine #MASS所带数据
-
attach(quine)#把数据变量的名字放入内存
-
#下面是从该数据得到的各种表格
-
table(Age)
-
table(Sex, Age); tab=xtabs(~ Sex + Age, quine); unclass(tab)
-
tapply(Days, Age, mean)
-
tapply(Days, list(Sex, Age), mean)
-
detach(quine) #attach的逆运行
实践19: 如何写函数
-
ss=function(n=100){z=2;
-
for (i in 2:n)if(any(i%%2:(i-1)==0)==F)z=c(z,i);return(z) }
-
#fix(ss) #用来修改任何函数或编写一个新函数
-
ss() #计算100以内的素数
-
t1=Sys.time() #记录时间点
-
ss(10000) #计算10000以内的素数
-
Sys.time()-t1 #费了多少时间
-
system.time(ss(10000))#计算执行ss(10000)所用时间
-
#函数可以不写return,这时最后一个值为return的值.
-
#为了输出多个值最好使用list输出
实践20: 画图
-
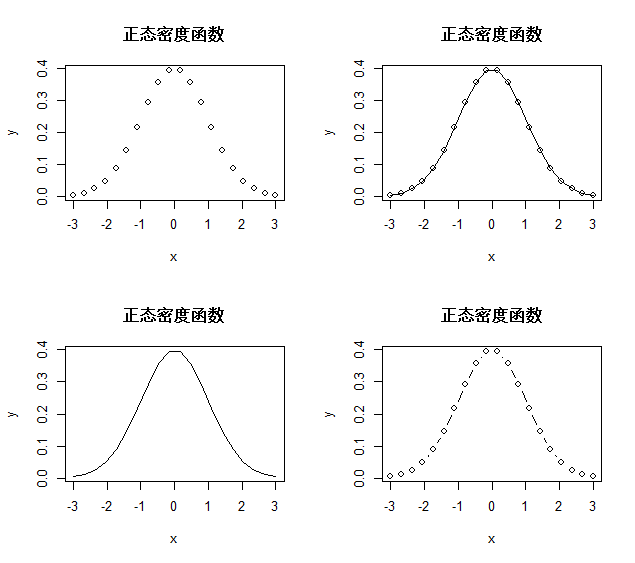
x=seq(-3,3,len=20);y=dnorm(x)#产生数据
-
w= data.frame(x,y)#合并x,成为数据w
-
par(mfcol=c(2,2))#准备画四个图的地方
-
plot(y ~ x, w,main="正态密度函数")
-
plot(y ~ x,w,type="l", main="正态密度函数")
-
plot(y ~ x,w,type="o", main="正态密度函数")
-
plot(y ~ x,w,type="b",main="正态密度函数")
-
par(mfcol=c(1,1))#取消par(mfcol=c(2,2))
实践21: 色彩和符号等调节
-
plot(1,1,xlim=c(1,7.5),ylim=c(0,5),type="n") #画出框架
-
#在plot命令后面追加点(如要追加线可用lines函数):
-
points(1:7,rep(4.5,7),cex=seq(1,4,l=7),col=1:7, pch=0:6)
-
text(1:7,rep(3.5,7),labels=paste(0:6,letters[1:7]),cex=seq(1,4,l=7),
-
col=1:7)#在指定位置加文字
-
points(1:7,rep(2,7), pch=(0:6)+7)#点出符号7到13
-
text((1:7)+0.25, rep(2,7), paste((0:6)+7))#加符号号码
-
points(1:7,rep(1,7), pch=(0:6)+14) #点出符号14到20
-
text((1:7)+0.25, rep(1,7), paste((0:6)+14)) #加符号号码
-
#这些关于符号形状, 大小, 颜色以及其它画图选项的说明可用"?par"来查看
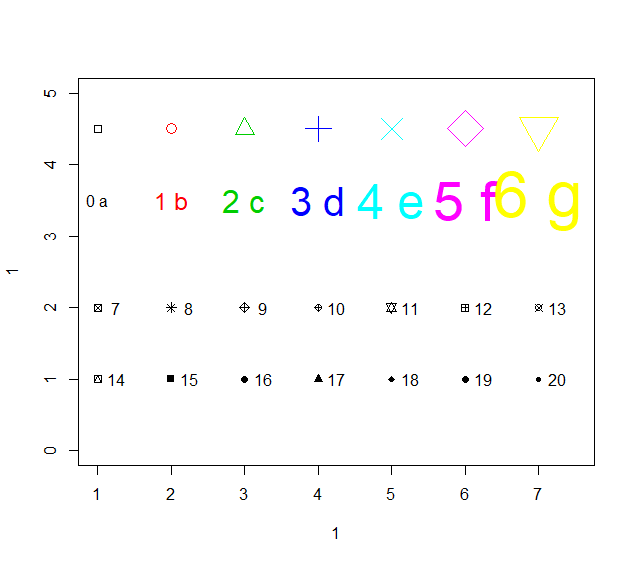
文章来源: drugai.blog.csdn.net,作者:DrugAI,版权归原作者所有,如需转载,请联系作者。
原文链接:drugai.blog.csdn.net/article/details/86512945
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)