@Author：Runsen

@Date：2020/9/10

现在大四基本是重刷数据结构和算法，因为笔试真的太重要了。 Runsen又重温了争大佬专栏的队列，又巩固了下。而且Runsen发现留言区大佬的笔记很多，下面很多都是来自大佬总结的。

树：

节点的高度=节点到叶子节点的最长路径（边数）
节点的深度=根节点到这个节点所经历的边的个数
节点的层数=节点的深度 + 1
树的高度=根节点的高度

二叉树：

1，二叉树，每个节点最多有两个叉，即两个子节点，分布是左子节点和右子节点。
2，二叉树不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点。

3，满二叉树：叶子节点全部都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫做满二叉树。
4，完全二叉树：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大。
5，二叉树的表示和储存方式：

①：存储一颗二叉树，有两种方法：
基于指针或者引用的二叉链表存储法；
基于数组的顺序存储法

②：链式存储法：

每个节点有三个字段，其中一个存储数据，另两个指向左右子节点的指针。这种存储方式比较常用。

③：顺序存储法

把根节点存储在下标i=1的位置，左子节点存储在下标 2i=2的位置，右子节点存储在2 * I +1=3的位置。以此类推。
如果节点X存储在数组中下标为i的位置，下标2i的位置存储的就是左子节点，下标为2*I +1的位置存储的就是右子节点。
反之，下标为i/2的位置存储就是他的父节点。通过这种方式，只要知道根节点存储位置，就可以通过下标计算，把整棵树都串起来。
使用数组储存二叉树，如果是一课完全二叉树，所以仅“浪费”一个下标为0的存储位置。如果是非完全二叉树，会浪费比较多的数组存储空间。

④：完全二叉树
如果某颗二叉树是一课完全二叉树，那用数组存储是最节省内存的一种方式。因为数组存储方式不需要像链式存储法那样，要存储额外的左右子节点的指针。这个是完全二叉树要求最后一层子节点都靠左的原因。
堆其实也是一种完全二叉树，最常用的存储方式就是数组。

二叉树的遍历

二叉树遍历是非常常见的面试题，将所有节点都遍历打印出来的经典方法有三种：前序遍历，中序遍历，后序遍历。其中，前，中，后序，表示的是节点于它的左右子树节点遍历打印的先后顺序。

①：前序遍历：
对于树中的任意节点来将，先打印这个节点，然后在打印它的左子树，最后打印它的右子树。
②：中序遍历：
对于树中的任意节点来说，先打印它的左子树，然后在打印它本身，最后打印它的右子树。
③：后序遍历：
对于树中的任意节点来说，先打印它的左子树，然后在打印它的右子树，最后打印这个节点本身。

实际上，二叉树的前，中，后遍历就是一个递归的过程。

前序遍历的递推公式：

preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)

  

 

  
1
 

具体实现代码：Leetcode 144. 二叉树的前序遍历

class Solution: def preorderTraversal(self, root: TreeNode) -> List[int]: res = [] def dfs(root): if not root: return [] res.append(root.val) dfs(root.left) dfs(root.right) dfs(root) return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

中序遍历的递推公式：

inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)、

  

 

  
1
 

具体实现代码：Leetcode 94. 二叉树的中序遍历

class Solution: def inorderTraversal(self, root: TreeNode) -> List[int]: res = [] def dfs(root): if not root: return [] dfs(root.left) res.append(root.val) dfs(root.right) dfs(root) return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
 

后序遍历的递推公式：

postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

  

 

  
1
 

具体实现代码：Leetcode 145. 二叉树的后序遍历

class Solution: def postorderTraversal(self, root: TreeNode) -> List[int]: res = [] def dfs(root): if not root: return [] dfs(root.left) dfs(root.right) res.append(root.val) dfs(root) return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

二叉树遍历的时间复杂度

每个节点最多会被访问两次，所以遍历操作的时间复杂度，更节点的个数n成正比，就是说二叉树遍历的时间复杂度是O(n)。

二叉树的遍历方式是最基本，也是最重要的一类题目，上面Runsen总结了「前序」、「中序」、「后序」、还剩一个「层序」遍历方式，方式就是使用双端队列。

下面具体二叉树层次遍历实现代码：Leetcode 102. 二叉树的层次遍历

class Solution: def levelOrder(self, root: TreeNode) -> List[List[int]]: ''' 使用双端队列，方便两端元素入队出队操作 遍历每一层前，记录当前层节点数量 n 具体处理每一个节点时，若它有孩子，则将它的孩子入队 当前层遍历结束后立即将结果存储到最终结果中 ''' if not root: return [] res,q = [],[root] while q: n =len(q) level = [] for i in range(n): node = q.pop(0) level.append(node.val) if node.left: q.append(node.left) # level.append(node.left) if node.right: q.append(node.right) # level.append(node.right) res.append(level) return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
 

上面代码是bfs的广度优先搜索。下面补充下dfs深度优先搜索解决层次遍历的方法。

class Solution: def __init__(self): self.res = [] #存储最终结果的大列表 #增加一个参数表示层级，注意使用参数形式传递，这样子不会有全局干扰 def levelOrder(self, root: TreeNode,level=0) -> List[List[int]]: #如果节点为空。直接返回一个空列表。根节点为空返回这个结果。子节点为空，相当于回退，不影响 if not root: return [] # print((root.val,level)) #调试用 #如果当前层的子列表不存在，先新增一个空列表,后续再根据层值去插值 if len(self.res) <= level: self.res.append([]) self.res[level].append(root.val) level += 1 #更新层级 self.levelOrder(root.left,level) self.levelOrder(root.right,level) return self.res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
 

在Leetcode中，Runsen发现了还有一个103. 二叉树的锯齿形层次遍历，也顺便搞定。

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如：
给定二叉树 [3,9,20,null,null,15,7], 3 / \
  9  20 /  \ 15   7
返回锯齿形层次遍历如下：

[
  [3],
  [20,9],
  [15,7]
]

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
 

这里和层次很像，就是多一个方向的判断，这里我直接用1表示右边，-1就是左边，这样使用列表切片可以反转。

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None

class Solution: def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]: """ :type root: TreeNode :rtype: List[List[int]] """ if not root: return [] res, level, direction = [], [root], 1 while level: res.append([n.val for n in level][::direction]) direction *= -1 # 这里的level 需要去除上面res添加的 level = [kid for node in level for kid in (node.left, node.right) if kid] return res


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
 

思考

给定一组数据，比如 1，3，5，6，9，10。你来算算，可以构建出多少种不同的二叉树？

结果是卡特兰数，是C[n,2n] / (n+1)种形状，c是组合数，节点的不同又是一个全排列，一共就是$n!\ast C[n,2n]/(n+1)$个二叉树。可以通过数学归纳法推导得出。

确定两点：

1）n个数，即n个节点，能构造出多少种不同形态的树？
2）n个数，有多少种不同的排列？

当确定以上两点，将【1)的结果】乘以 【2)的结果】，即为最终的结果。
但是有一个注意的点： 如果n中有相等的数，产生的总排列数就不是$n！$了哟

通过这一题，Runsen学到了【卡塔兰数】：https://en.wikipedia.org/wiki/Catalan_number

补充：

卡塔兰数，通常记作c(n)，是指n个A和n个B组成的这样的序列的数目，从前往后读，A的数目始终大于等于B。用组合数表示的话，c(n)=C(2n,n)/(n+1)。

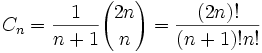
卡特兰数的前10项分别为：1、2、5、14、42、132、429、1430、4862。

与斐波那契数列（Fibonacci Sequence）一样，卡塔兰数也是离散数学和编程算法中相当重要的数列，它以比利时的数学家欧仁·查理·卡塔兰（Eugene Charles Catalan，1814年~1894年）命名。

Runsen不是学这方面的，看到文章底部有人说起，就百度了解下。

参考：极客时间王争大佬：https://time.geekbang.org/column/article/67856

文章来源: maoli.blog.csdn.net，作者：刘润森！，版权归原作者所有，如需转载，请联系作者。

原文链接：maoli.blog.csdn.net/article/details/108523378