@Author：Runsen

编程的本质来源于算法，而算法的本质来源于数学，编程只不过将数学题进行代码化。 ---- Runsen

本人看了vivo，阿里巴巴的校招算法题，可以明确知道绝对有动态规划。如果没有，那么出题的面试官真的没有水平。跌了N次的动态规划，Runsen最近也拼命搞动态规划。这篇文章浪费了三天时间。

看了Leetcode公众号的文章：https://mp.weixin.qq.com/s/rhyUb7d8IL8UW1IosoE34g

极客时间超哥的动态规划、拉勾教育的算法专栏。Runsen真的不想在动态规划，死一次又一次。死了N次，学了N次，就是他妈的写不出来。

动态规划需要搞定三个系列：三个背包，零钱问题和股票问题。今天，Runsen就开始干掉最重要的背包问题。

三个背包问题：01背包，多重背包，完全背包。

动态规划前置知识

动态规划的名词

状态转移方程：比如Runsen们一般看到的状态转移方程：dp[n] = dp[n-1] + dp[n-2]。

最优子结构：一般由最优子结构，推导出一个状态转移方程 f(n)，就能很快写出问题的递归实现方法。
把大问题变成几个小问题，在几个小问题中求出最佳解。

重叠子问题：比如斐波那契数列中的f(5)，算了f(4)和f(3)，结果f(4)又给Runsen算了一次f(3)。其实就是将一棵二叉树进行剪枝操作，方法是备忘录来存储在内存上。

自下而上：反过来求解

动态规划思路

动态规划是一种求问题最优解的方法。通用的思路：将问题的解转化成==> 求解子问题，==> 递推，==>最小子问题为可直接获得的初始状态。

详细的步骤下面所示：

• 判断是否可用递归来解，可以的话进入步骤 2
• 分析在递归的过程中是否存在大量的重复子问题
• 采用备忘录的方式来存子问题的解以避免大量的重复计算（剪枝）
• 改用自底向上的方式来递推，即动态规划

关键就是找状态转移方程。

斐波那契数列和爬楼梯问题

斐波那契数列最早从兔子问题演变过来的，

假设一对初生兔子一个月到成熟期，一对成熟兔子每月生一对兔子，并且一年内没有发生死亡。那么，由一对初生兔子开始
一年以后可以繁殖多少对兔子？

我们直接看下面的图

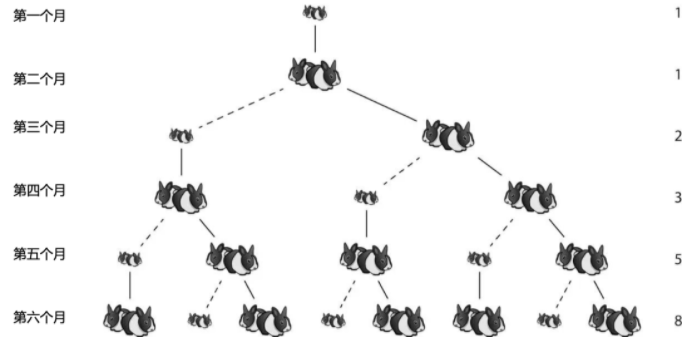
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……

发现以上规律是，每月的兔子对数=上一月的兔子对数＋该月新生的兔子对数=上一月的兔子对数＋上上月的兔子对数

得到序列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……

这个序列即为斐波那契数列“（Fibonacci sequence）”。斐波那契数列中的任一个数，都叫斐波那契数

斐波那契数列，通常都是用来讲解递归函数，尝试用递归的思路来解决，但是时间复杂度高达$O(2^n)$。

def fib(n):
  if n <= 1: return 1
  return fib(n-1) + fib(n-2)

for i in range(20): print(fib(i), end=' ')

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

但是，我们发现时间复杂度高达$O(2^n)$，最主要的原因是存在重复计算。比如fib(3) 会计算 fib(2) + fib(1)，
而 fib(2) 又会计算 fib(1) + fib(0)。

这个 fib(1) 就是完全重复的计算，不应该为它再递归调用一次，而是应该在第一次求解除它了以后，就把他“记忆”下来。

这就是备忘录解法，用空间来换取时间的思路。把已经求得的解放在字典Map或者列表list 里，下次直接取，而不去重复结算。

备忘录解法的代码和动态规划的代码和思路基本一致。

斐波那契数列在Leetcode也有一题类似的，这是Leetcode第70题. 爬楼梯，每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

  

 

  
1
  
2
  
3
  
4
  
5
 

斐波那契数列和爬楼梯问题的状态转移方程都是:dp[i] = dp[i-1] +dp[i-2]。但是需要初始化dp，不然回报list assignment index out of range的错误。

下面就是斐波那契数列问题 爬楼梯的解决代码，也是Leetcode70题的解决代码。

class Solution: def Fibonacci(self, n): if n == 0: return 1 if n == 1: return 1 if n > 1: dp = [0] * (n+1) dp[0] = 1 dp[1]= 1 for i in range(2,n+1): dp[i] = dp[i-1] +dp[i-2] return dp[n]

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

Leetcode53 最大子序和

最大子序和，Runsen记得很清楚是Leetcode的53题。

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

  

 

  
1
  
2
  
3
 

声明两个变量, currentSum: 之前连续几个值相加的和, maxSum: 当前最大的子序列和。最大子序和状态转移方程 f(i) = max(f(i), f(i)+nums[i+1])

def maxSubArray(nums) : '''查找连续子数组的最大和 Args: nums: 整数数组 Returns: 返回整数数组的最大子序和 ''' # 比较当前子序和，最大子序和，返回最大值 # 定义当前子序和以及最大子序和为第一个元素 cursum = maxsum = nums[0] for i in range(1, len(nums)): cursum = max(nums[i], cursum + nums[i]) print(cursum) # 比较当前值和定义的最大子序和值，将最大值重置赋值给 max_sum maxsum = max(cursum, maxsum) print(maxsum) return maxsum

print(maxSubArray([-2,1,-3,4,-1,2,1,-5,4]))

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
 

前面只是动态规划的热身，Runsen先进入三个背包问题的强化系列，01背包问题才是动态规划的入门阶段。

01背包问题

对应的题目：https://www.acwing.com/problem/content/2/

01背包问题就是物品只有一件。

输入格式 : 第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。 
输出格式 : 输出一个整数，表示最大价值。 
数据范围 : 0<N,V≤1000  ；0<vi,wi≤1000

  

 

  
1
  
2
  
3
 

输入样例

4 5
1 2
2 4
3 4
4 6

  

 

  
1
  
2
  
3
  
4
  
5
 

输出样例：

8 # 4+4 2+6

  

 

  
1
 

在解决这类问题先，dp怎么定义和状态转移方程怎么搞就是重要，搞定了就是半分钟的事情。搞不定了可能半小时的事情。

很多人和Runsen一样，都会把状态定义二维数组：$dp[i][v]$ 为前 $i$ 「个」 物品中，体积恰好为$v$ 时的最大价值。

状态转移方程也是顺便搞定：$$dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])$$

如果 「不选第 i 个物品」，那么前 i 个背包的最大价值就是前 i-1 个物品的价值，即 dp[i][j] = dp[i-1][j]；

如果 「选择了第 i 个物品」，前 i-1 个物品的体积就是j - weight[i]，状态方程为 dp[i - 1][j - weight[i]] + value[i]，注意这时的价值是前i-1个物品的价值，因此少了 weight[i]]的空间，所以 dp[i - 1][j - weight[i]] + value[i]。

'''
@Author： Runsen
@WeChat：RunsenLiu 
@微信公众号： Python之王
@CSDN： https://blog.csdn.net/weixin_44510615
@Github： https://github.com/MaoliRUNsen
@Date： 2020/9/10
'''
# n是个数 v是体积  # 4 5
n, v = map(int, input().split())
goods = []
for i in range(n): goods.append([int(i) for i in input().split()])

# 初始化，先全部赋值为0，这样至少体积为0或者不选任何物品的时候是满足要求
# 因为for 循环先遍历个数，所以将体积写在里面
dp = [[0 for i in range(v+1)] for j in range(n+1)]
print(goods) # [[1, 2], [2, 3], [3, 4], [4, 5]]
# 0 可以无视掉
for i in range(1, n+1): for j in range(1,v+1): # 判断背包容量是不是大于第i件物品的体积 if j>=goods[i-1][0]: # 在选和不选的情况中选出最大值 dp[i][j] = max(dp[i-1][j], dp[i - 1][j - goods[i - 1][0]] + goods[i - 1][1]) else: # 第i个物品不选 dp[i][j] = dp[i-1][j]  
print(dp)
print(dp[-1][-1])

# 测试数据
5 10
1 2
2 3
3 4
4 5
5 6
[[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]]
[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], [0, 2, 3, 5, 5, 5, 5, 5, 5, 5, 5], [0, 2, 3, 5, 6, 7, 9, 9, 9, 9, 9], [0, 2, 3, 5, 6, 7, 9, 10, 11, 12, 14], [0, 2, 3, 5, 6, 7, 9, 10, 11, 12, 14]]
14  # 2+3+4+5

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
 

上面代码，如果知道了dp怎么定义和状态转移方程，那么和Runsen写的一样快，其实那时Runsen写得挺慢得，说不定你比Runsen还厉害。

上面的代码是状态定义二维数组，有的大佬竟然可以把状态定义一维数组，这样空间就节省了。Runsen都百思不知其解。只能说Runsen真的挺菜的。只好勤能补拙！

一维数组就是去掉了状态$i$，且$j$的遍历方式改为 「倒序」 遍历到 c[i]。

因此，Runsen们可以将求解空间进行优化，将二维数组压缩成一维数组，此时，转移方程变为：

$$dp(j)=max(dp(j),dp(i-wi)+vi)$$

'''
@Author： Runsen
@WeChat：RunsenLiu 
@微信公众号： Python之王
@CSDN： https://blog.csdn.net/weixin_44510615
@Github： https://github.com/MaoliRUNsen
@Date： 2020/9/10
'''
n, v = map(int, input().split())
goods = []
for i in range(n): goods.append([int(i) for i in input().split()])
print(goods) # [[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]]
dp = [0 for i in range(v + 1)]
for i in range(n): # 由于要放入物品，所以从空间v开始遍历到0 for j in range(v, -1, -1): # 判断背包容量是不是大于第i件物品的体积 if j >= goods[i][0]: # 更新j的状态，即当前容量放入物品之后的状态 dp[j] = max(dp[j], dp[j - goods[i][0]] + goods[i][1])
print(dp)
print(dp[-1])

5 10
1 2
2 3
3 4
4 5
5 6
[[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]]
[0, 2, 3, 5, 6, 7, 9, 10, 11, 12, 14]
14

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
 

上面就是01背包的最终解决方法，由于文章有限，多重背包，完全背包将在之后的博客进行书写！！！

不知不觉现在写了几天，代码反复写，写完写博客，真心累！谁叫自己的算法比较弱！

希望以后遇到01背包的问题，就是在恐怖的算法面试中遇见了Runsen的爱情！

如果你想跟博主建立亲密关系，可以关注博主，或者关注博主公众号“Python之王”，了解一个非本科程序员是如何成长的。博主ID：润森（weixin_44510615），希望大家点赞、评论、收藏

本文已收录 GitHub，传送门~ ，里面更有大厂面试完整考点，欢迎 Star。

文章来源: maoli.blog.csdn.net，作者：刘润森！，版权归原作者所有，如需转载，请联系作者。

原文链接：maoli.blog.csdn.net/article/details/108432363