@Author：Runsen

81、逆序对

逆序对应的题目来源：Leetcode剑指 Offer 51. 数组中的逆序对

"""
@Author：Runsen
一、逆序数： 给定一个数组array[0,...,n-1], 若对于某两个元素array[i],array[j],若i<j and array[i]>array[j], 则认为array[i],array[j]是逆序对。一个数组中包含的逆序对的数目称为该数组的逆序数。设计一个算法求一个数组的逆序数
二、利用 归并排序 的思想 在归并排序中，会将两个升序的数组进行合并，利用升序数组的特性，可以快速求得逆序数
"""

class Solution: def reversePairs(self, nums: List[int]) -> int: self.cnt = 0 def merge(nums, start, mid, end, temp): i, j = start, mid + 1 while i <= mid and j <= end: if nums[i] <= nums[j]: temp.append(nums[i]) i += 1 else: self.cnt += mid - i + 1 temp.append(nums[j]) j += 1 while i <= mid: temp.append(nums[i]) i += 1 while j <= end: temp.append(nums[j]) j += 1 for i in range(len(temp)): nums[start + i] = temp[i] temp.clear() def mergeSort(nums, start, end, temp): if start >= end: return mid = (start + end) >> 1 mergeSort(nums, start, mid, temp) mergeSort(nums, mid + 1, end, temp) merge(nums, start, mid,  end, temp) mergeSort(nums, 0, len(nums) - 1, []) return self.cnt

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
 

82、手写一个栈

顺序栈是使用顺序表存储数据的栈，在很多面试中需要手写一个栈。

class Stack(object): def __init__(self): """ 创建一个Stack类 对栈进行初始化参数设计 """ self.stack = [] #存放元素的栈
​ def push(self, data): """ 压入 push ：将新元素放在栈顶 当新元素入栈时，栈顶上移，新元素放在栈顶。 """ self.stack.append(data)
​ def pop(self): """ 弹出 pop ：从栈顶移出一个数据 - 栈顶元素拷贝出来 - 栈顶下移 - 拷贝出来的栈顶作为函数返回值 """ # 判断是否为空栈 if self.stack: return self.stack.pop() else: raise IndexError("从空栈执行弹栈操作")
​ def peek(self): """ 查看栈顶的元素 """ # 判断栈是否为空 if self.stack: return self.stack[-1]
​ def is_empty(self): """ 判断栈是否为空 """ # 栈为非空时，self.stack为True，再取反，为False return not bool(self.stack)
​ def size(self): """ 返回栈的大小 """ return len(self.stack)

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
 

83、有效的扩号

这是Leetcode的第20题。给定一个只包括'('，')'，'{'，'}'，'['，']'的字符串，判断字符串是否有效。

'''
@Author： Runsen
@WeChat：RunsenLiu 
@微信公众号： Python之王
@CSDN： https://blog.csdn.net/weixin_44510615
@Github： https://github.com/MaoliRUNsen
@Date： 2020/9/8
'''
class Solution: def isValid(self, s: str) -> bool: stack = [] d = {"{": "}", "[": "]", "(": ")"} for i in s: if i in d: stack.append(i) else: # 记住如果使用了stack.pop() 那么就已经默认删除了 pop这里已经执行了 # 还有not stack和 len(stack) == 0等价 if  (len(stack) == 0) or (d[stack.pop()] != i): return False return len(stack) == 0 

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
 

84、扩号的生成

这是Leetcode的第22题。数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

class Solution: def generateParenthesis(self, n: int) -> List[str]: res = [] # 回溯算法 # 括号生成第一个必须是左括号，那么下一个可能是左括号和右括号， def g(left,right,n,result): if left == n and right == n: res.append(result) if left < n: g(left+ 1,right,n,result + "(") # 有效的前提需要左括号大于右括号 if left > right and right < n: g(left,right+ 1,n,result + ")") g(0,0,n,"") return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
 

85、最长有效括号

这是Leetcode的第32题。给定一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。

这道题在今年的秋招中见过，而且牛客在每周的周四算法面试题也讲过。解决的方法就是动态规划和栈。

栈的方法很容易想到，九月份我用的栈方法通过AC。

class Solution: def longestValidParentheses(self, s: str) -> int: ''' @Author：Runsen 思路：对于遇到的每个 ‘(’ ，我们将它的下标放入栈中
对于遇到的每个 ‘)’ ，我们先弹出栈顶元素表示匹配了当前右括号：
如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
如果栈不为空，当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」 ''' if not s: return 0 stack = [] res= 0 for i in range(len(s)): # 入栈条件 if not stack or s[i] == '(' or s[stack[-1]] == ')': stack.append(i) # 下标入栈 else: # 计算结果 stack.pop() res = max(res, i - (stack[-1] if stack else -1)) return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
 

对于dp，这里分两种情况，一个是，s[i]=‘)’ 且s[i - 1] =‘(’，也就是字符串形如 “……()”“……()”，我们可以推出dp[i] = dp[i -2]+2。

还有一个是，s[i]=‘)’ 且 s[i - 1] = ‘)’，也就是字符串形如 “……))”，可以推出：dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] +2。

这里状态转移方程不好理解，建议去官网查看

class Solution: def longestValidParentheses(self, s: str) -> int: maxans = 0 dp = [0]*len(s) for i in range(len(s)): if s[i] == ")": if s[i - 1] == "(": dp[i] = (dp[i -2] if i >= 2 else 0 ) + 2 elif i - dp[i - 1] > 0 and s[i - dp[i - 1] - 1] == "(": dp[i] = dp[i - 1] + (dp[i - dp[i - 1] - 2] if i - dp[i - 1] >= 2 else 0) +2 maxans = max(maxans, dp[i]) return maxans

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
 

86、比特位计数问题

在阿里笔试比较常见二进制和丑数等数学的问题。

这是Leetcode338面试题比特位计数：给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

输入: 2
输出: [0,1,1]
示例 2:

输入: 5
输出: [0,1,1,2,1,2]

最快速的方法就是直接count进行计数就可以了。

class Solution: def countBits(self, num: int) -> List[int]: res = [] for i in range(num+1): count = bin(i).count("1") res.append(count) return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

但很多的时候，面试官要求换一个思路，其实就是动态规划

观察：
十进制0： 二进制0
十进制1： 二进制1
十进制2： 二进制10
十进制3： 二进制11
十进制4： 二进制100
十进制5： 二进制101

二进制中，乘以2相当于左移一位，1的个数不会改变；
由于偶数的二进制形式结尾一定是0，所以一个偶数加1变为奇数，只会将其结尾的0变为1；

所以状态转移方程为：
$dp(i)=dp(i//2)$ 若i为偶数； 这里//2保证是整数，防止溢出

$dp(i)=dp(i-1)+1$ 若i为奇数。

边界条件： dp(0) = 0。最后利用二进制方法将两个判断合并起来得到dp[i] = dp[i>>1] + (i&1)，这里 i>>1代表前一个二进制位的次数,i&1代表i的末尾是否为1

class Solution: def countBits(self, num: int) -> List[int]: dp = [0] for i in range(1, num + 1): dp.append(dp[i>>1] + (i&1)) return dp

  

 

  
1
  
2
  
3
  
4
  
5
  
6
 

87、判断给定的数是否为丑数

这是Leetcode 263：判断给定的数是否为丑数：编写一个程序判断给定的数是否为丑数。丑数就是只包含质因数 2, 3, 5 的正整数。

此题是简单题：一个思路是递归，一个思路就是直接暴力。

第一步：只要num大于5（2,3,5中5最大）就继续循环。
第二步：只要num不能整除其中三个数任意一个，就返回False。
第三步：继续除以可以整除的循环。
备注：这里需要注意的是题目中“1”是返回True。

# 递归的做法
class Solution: def isUgly(self, num: int) -> bool: if num <= 0: return False elif num <=6 : return True if num % 2 == 0: return self.isUgly(num / 2) if num % 3 == 0: return self.isUgly(num / 3) if num % 5 == 0: return self.isUgly(num / 5) return False


# while循环暴力破解
class Solution: def isUgly(self, num: int) -> bool: if num <= 0: return False while num >= 5: if num % 2 != 0 and num % 3 != 0 and num % 5 != 0: return False else: if num % 2 == 0: num = num // 2 elif num % 3 == 0: num = num // 3 else: num = num //5 return True



  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
 

88、找出第 n 个丑数

这是Leetcode 264：找出第 n 个丑数：编写一个程序，找出第 n 个丑数。丑数就是质因数只包含 2, 3, 5 的正整数。

Leetcode 264：

示例:

输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

  

 

  
1
  
2
  
3
  
4
  
5
  
6
 

此题是一个我想不到的dp。想一想丑数肯定是一个来源2，3，5 其中一个倍数，然后就是每次选出最小的丑数并添加到数组中。并将该丑数对应的因子指针往前走一步。重复该步骤直到计算完 。对应的dp状态转移方程：min(res[i2] * 2, res[i3] * 3, res[i5] * 5)

class Solution: def nthUglyNumber(self, n: int) -> int: res = [1] # 三指针 i2 = i3 = i5 = 0 for _ in range(1,n): ugly = min(res[i2] * 2, res[i3] * 3, res[i5] * 5) res.append(ugly) if ugly == res[i2] * 2: i2 +=1 if ugly == res[i3] * 3: i3 +=1 if ugly == res[i5] * 5: i5 +=1 return res[-1]

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
 

89、超级丑数

这是Leetcode 313：超级丑数：编写一个程序，找出超级丑数，只不过因子变了。

示例:

输入: n = 12, primes = [2,7,13,19]
输出: 32 
解释: 给定长度为 4 的质数列表 primes = [2,7,13,19]，前 12 个超级丑数序列为：[1,2,4,7,8,13,14,16,19,26,28,32] 。

  

 

  
1
  
2
  
3
  
4
  
5
 

方法和上面三指针的dp完全一样。我们在寻找新的超级丑数的时候，只需要寻找M，并选择M数组中最小的一个数来作为这个新的超级丑数就好了。

其实没什么难度，算法的小逻辑做了一些调整，但是算法的思路并没有改变。

class Solution: def nthSuperUglyNumber(self, n: int, primes: List[int]) -> int: nums = [0 for _ in range(len(primes))] result = [1] for i in range(1,n): ugly = min(result[nums[j]] * primes[j] for j in range(len(nums))) result.append(ugly) for k in range(len(nums)): if ugly == result[nums[k]] * primes[k]: nums[k] +=1 return result[-1]

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

90、合并区间

这是Leetcode 56：合并区间：给出一个区间的集合，请合并所有重叠的区间。

示例 1:

输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

  

 

  
1
  
2
  
3
  
4
  
5
 

原理就是：新的区间左边的数字为原第一个区间左边的数字，新区间右边的数字为 原第一个区间右边数字和原第二个区间右边数字的最大值。

class Solution: def merge(self, intervals: List[List[int]]) -> List[List[int]]: if not intervals: return [] # 对区间进行排序 intervals.sort(key=lambda x:x[0]) res = [intervals[0]] for i in range(1,len(intervals)): if intervals[i][0] <= res[-1][1]: res[-1] = [res[-1][0], max(intervals[i][1], res[-1][1])] else: res.append(intervals[i]) return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
 

91、区间列表的交集

这是Leetcode986 ：区间列表的交集：给定两个由一些 闭区间 组成的列表，每个区间列表都是成对不相交的，并且已经排序。

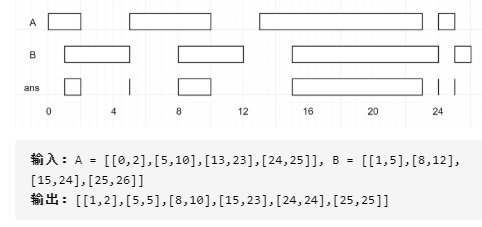
区间列表的交集，一个双指针。关键就是最后一步，指针i和j什么时候应该前进呢？只要判断两个数组右指针的大小可以 了。

class Solution: def intervalIntersection(self, A: List[List[int]], B: List[List[int]]) -> List[List[int]]: i, j = 0, 0 # 双指针 res = [] while i < len(A) and j < len(B): a1, a2 = A[i][0], A[i][1] b1, b2 = B[j][0], B[j][1] # 两个区间存在交集 if b2 >= a1 and a2 >= b1: # 计算出交集，加入 res res.append([max(a1, b1), min(a2, b2)]) # 指针前进 if b2 < a2: j += 1 else: i += 1 return res

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
 

92、删除被覆盖区间

这是Leetcode1288：删除被覆盖区间：给你一个区间列表，请你删除列表中被其他区间所覆盖的区间。

示例：

输入：intervals = [[1,4],[3,6],[2,8]]
输出：2
解释：区间 [3,6] 被区间 [2,8] 覆盖，所以它被删除了。

class Solution: def removeCoveredIntervals(self, intervals: List[List[int]]) -> int: # 排序 intervals.sort(key = lambda x: (x[0], -x[1])) count = 0 prev_end = 0 for _, end in intervals: if end > prev_end: count += 1 prev_end = end return count		

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

93、最长上升子序列

这是Leetcode300：最长上升子序列：给定一个无序的整数数组，找到其中最长上升子序列的长度。

输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

关键还是怎么找出dp和转移方程，dp[i]是第i个最长上升子序列。那么$dp[i]=max(dp[i],dp[k]+1)其中0<k<i-1$

class Solution: def lengthOfLIS(self, nums: List[int]) -> int: # 如果定义dp dp[i] 最长上升子序列 那么 dp[i] = max(dp[i], dp[k] + 1)  0<k<i-1 m = len(nums) if m <= 1: return  m dp = [ 1 for _ in range(m)] for i in range(1,m): for j in range(i): if nums[i] > nums[j]: dp[i] = max(dp[i], dp[j]+ 1 ) return max(dp)


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
 

94、接雨水

这是Leetcode 42 ：接雨水：给定 n 个非负整数表示每个宽度为 1 的柱子的高度，计算按此排列的柱子，下雨之后能接多少雨水。

本题的关键点在于，具备什么条件的格子可以存水？

(1) 空间未被柱子占据；(2) 左右两侧均有比当前位置高或者等于的柱子。

其实就是寻找凹陷的地方。常规做法就是找到最高的柱子，分成两份，寻找凹陷的地方。

# @Author：Runsen
# @Date：2020/09/30

class Solution: def trap(self, height: List[int]) -> int:
		# 寻找最大的柱子 maxindex = maxvalue = 0 n = len(height) for i in range(n): if height[i] > maxvalue: maxvalue = height[i] maxindex = i # 左边找凹槽 a = res = 0 for i in range(maxindex): if a < height[i]: a = height[i] continue res = res + a - height[i] # 右边找凹槽 b = 0 for i in range(n-1,maxindex,-1): if b < height[i]: b = height[i] continue res = res + b - height[i] return res


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
 

95、逛街

逛街此题来源于牛客，是今年秋招一个题目。

题目描述：输出一行，包含空格分割的n个数字vi，分别代表小Q在第i栋楼时能看到的楼的数量。

输入

6
5 3 8 3 2 5

  

 

  
1
  
2
 

输出：3 3 5 4 4 4

逛街此题最简单易懂的方法使用单调栈，

n = int(input())
a = list(map(int, input().split()))
# left right为栈
left = []
right = []
# l_num左边看到的楼层
l_num = []
# r_num右边看到的楼层
r_num = []
for i in range(len(a)):  # 向左看 l_num.append(len(left)) if (i == 0):  # 第一个值特殊处理 left.append(a[i]) elif (a[i] < left[-1]):  # 入栈操作 left.append(a[i]) else: while (len(left) != 0 and a[i] >= left[-1]): left.pop(-1) left.append(a[i])
# 将a进行翻转，进行向右看
a.reverse()
for i in range(len(a)):  # 向右看 r_num.append(len(right)) if (i == 0):  # 第一个值特殊处理 right.append(a[i]) elif (a[i] < right[-1]):  # 入栈操作 right.append(a[i]) else: while (len(right) != 0 and a[i] >= right[-1]): right.pop(-1) right.append(a[i])
# r_num也要翻转
r_num.reverse()
ans = []
for i in range(len(a)): ans.append(l_num[i] + r_num[i] + 1)
ansstr = ' '.join([str(i) for i in ans])
print(ansstr)

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
 

96、滑动窗口的最大值

这是Leetcode 239 ：滑动窗口的最大值：给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

'''
@Author： Runsen
@WeChat：RunsenLiu 
@微信公众号： Python之王
@CSDN： https://blog.csdn.net/weixin_44510615
@Github： https://github.com/MaoliRUNsen
@Date： 2020/9/8

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释: 滑动窗口的位置 最大值
--------------- -----
[1  3  -1] -3  5  3  6  7 3
 1 [3  -1  -3] 5  3  6  7 3
 1  3 [-1  -3  5] 3  6  7 5
 1  3  -1 [-3  5  3] 6  7 5
 1  3  -1  -3 [5  3  6] 7 6
 1  3  -1  -3  5 [3  6  7] 7
 
'''

def maxSlidingWindow(nums,k): if not  nums: return [] window ,res = [],[] for i,x in enumerate(nums): # 如果存在窗口 而且窗口的第一个数 不在这个范围，就出去 if i >= k and window[0] <= i-k: window.pop(0) # 每次进入窗口的和最后一个比较，如果大了，最后一个直接删除 while window and nums[window[-1]] <= x: window.pop() # 无论是不是删除最后一个，都要加入x到窗口中 window.append(i) # 如果出了窗口，就把窗口的头加入到res中 if i >= k-1: res.append(nums[window[0]]) print(window) return res

print(maxSlidingWindow(nums = [1,3,-1,-3,5,3,6,7],  k = 3))


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
 

97、最长回文子串

这是Leetcode 5 ：最长回文子串：给定一个字符串 s，找到 s 中最长的回文子串。

最长回文子串应该采取 中心扩散的思想，最后需要判断回文的长度是奇数还是偶数的情况，如果是奇数形回文，就以当前字符为中心左右两边寻找，例如回文"bab"；如果是偶数形回文，需要两个字符，并且这两个字符是相等的，则需要以当前字符和其相邻的字符为中心向左右两边寻找，例如回文"abba"。

class Solution: def longestPalindrome(self, s: str) -> str: def helper(s, l, r): # 中心扩散 while l >= 0 and r < len(s) and s[l] == s[r]: l -= 1 r += 1 return s[l + 1:r] res = "" for i in range(len(s)): # 奇数形回文, like "aba" tmp = helper(s, i, i) if len(tmp) > len(res): res = tmp # 偶数形回文, like "abba" tmp = helper(s, i, i + 1) if len(tmp) > len(res): res = tmp return res


  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
 

98、 回文子串

这是Leetcode 647：最长回文子串：计算这个字符串中有多少个回文子串

class Solution(object): def countSubstrings(self, s): """ :type s: str :rtype: int """ # 遍历s，将每个位置的字符当做回文中心扩散 n = len(s) # 一个字符也算是回文，所以开局count就是s中字符的数量 count = n for i in range(n): # 如果有两个相同的字符，那么将这两个相同字符作为回文中心扩散 if i+1 < n and s[i+1] == s[i]: count += 1 left, right = i-1, i+2 while left >= 0 and right < n and s[left] == s[right]: count += 1 left -= 1 right += 1 # 以当前字符作为回文中心开始扩散 left, right = i-1, i+1 while left >= 0 and right < n and s[left] == s[right]: count += 1 left -= 1 right += 1 return count

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
 

99、编辑距离

这是Leetcode 72：编辑距离：给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 (替换，删除，插入）。

编辑距离考察的是二维动态规划。dp[i][j]代表 word1到i位置转换成word2 到j位置需要最少步数。

所以，当word1[i] == word2[j]，dp[i][j] = dp[i-1][j-1]；当 word1[i] != word2[j]，dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1。其中，dp[i-1][j-1]表示替换操作，dp[i-1][j]表示删除操作，dp[i][j-1]表示插入操作。

class Solution: def minDistance(self, word1: str, word2: str) -> int: n1 = len(word1) n2 = len(word2) dp = [[0] * (n2 + 1) for _ in range(n1 + 1)] # 第一行 for j in range(1, n2 + 1): dp[0][j] = dp[0][j-1] + 1 # 第一列 for i in range(1, n1 + 1): dp[i][0] = dp[i-1][0] + 1 for i in range(1, n1 + 1): for j in range(1, n2 + 1): if word1[i-1] == word2[j-1]: dp[i][j] = dp[i-1][j-1] else: dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1] ) + 1 #print(dp)  return dp[-1][-1]

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
 

100、岛屿个数

这是Leetcode 200：岛屿个数：给定一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，

这题如果使用DFS比较简单，我们需要找到所有的连着的"1"，然后答案自增1，后面继续寻找没有被访问过了"1"，我们可以把访问过了的"1"变成"0"，因为我们对"0"的区域没有做任何操作。

class Solution: def numIslands(self, grid: List[List[str]]) -> int: if not grid: return 0 count = 0 for i in range(len(grid)): for j in range(len(grid[0])): if grid[i][j] == '1': self.dfs(grid, i, j) count += 1 return count def dfs(self, grid, i, j): if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] != '1': return grid[i][j] = '0' self.dfs(grid, i + 1, j) self.dfs(grid, i - 1, j) self.dfs(grid, i, j + 1) self.dfs(grid, i, j - 1)

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
 

岛屿个数的问题其实是引出并查集的算法，更多的解法查看Leetcode官网

如果你想跟博主建立亲密关系，可以关注博主，或者关注博主公众号“Python之王”，了解一个非本科程序员是如何成长的。
博主ID：润森，希望大家点赞、评论、收藏

文章来源: maoli.blog.csdn.net，作者：刘润森！，版权归原作者所有，如需转载，请联系作者。

原文链接：maoli.blog.csdn.net/article/details/108901896