RDKit | RDKit处理graph-化合物的邻接矩阵、距离矩阵和维纳指数

化合物的图（graph）表示

图可以表示一个原子与另一个原子的连接方式。 只有原子的连接和拓扑结构是重要的，而不是键距。

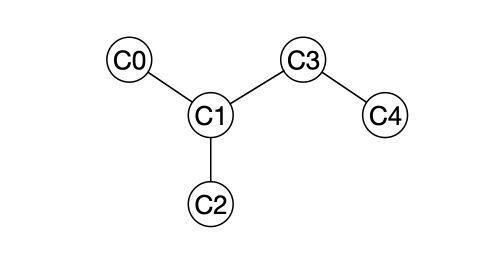
邻接矩阵

两个原子之间：

• 如果有结合，则为1；
• 如果没有结合，则为0。

那么，所有的原子间键都可以用下面的矩阵来表示。 这样的表示方法称为图的 "邻接矩阵"（adjacency matrix）。 当有两个键时，有时会用到2。

每个原子所连接的键数称为原子的 "度"（degree）。 根据定义，相邻矩阵是对称的。

距离矩阵

描述两个原子之间最短距离的矩阵称为 "距离矩阵"。 这种情况下，距离是一个拓扑距离，表示连接了多少条边。

对于异戊烷，如前所述，可表示如下： 距离矩阵也是一个对称矩阵。

文章来源: drugai.blog.csdn.net，作者：DrugAI，版权归原作者所有，如需转载，请联系作者。

原文链接：drugai.blog.csdn.net/article/details/109412338