NIPS2020 | DiffGCN：利用微分算子和代数多重网格池化优化图卷积

今天给大家介绍以色列本·古里安大学的研究人员发表在NIPS2020上的一篇论文。图卷积网络（GCN）在处理无序数据（如点云和网格）方面已被证明是有效的方法，作者在有限差分和代数多重网格框架的启发下，提出了用于图卷积，池化和解池化的新颖方法——DiffGCN，经各种实验证明，DiffGCN拥有最好的结果。

介绍

过去的几年中，许多工作使用标准的CNN对无序数据（例如点云和网格）执行3D相关任务。随后，GCN也用于处理与三维输入相关的任务，通过直接在数据的基础结构中进行操作，更加自然地处理非结构化数据。

这项工作中，作者利用标准CNN与偏微分方程（PDE）之间的相似性，提出了一种基于非结构化网格上的差分算子离散化图卷积方法，此类方法用于非结构化网格会导致卷积运算的抽象参数化，而该参数化与特定图形的几何形状无关。除此之外，作者还利用代数多重网格方法，提出了新颖的池化和解池化操作，可以扩大神经元感受野，降低计算成本，从从而可以实现更宽和更深的网络。

模型

作者根据图上定义的离散微分算子对图卷积核进行参数化，因此，将这种卷积称为DiffGCN。为了拥有完整的神经网络构建模块，作者还提出了AMG启发性的池化和解池算子，以扩大神经元的接受范围，并允许更广和更深的网络。

通过微分运算符进行卷积核 作者利用简单的算子来估计图上定义的非结构化特征图的梯度和拉普拉斯算子，给定无向图G =（V，E），其中V，E分别表示图的顶点和边，卷积核的公式如下，该核由图上定义的信号质量，梯度和拉普拉斯算子组成。

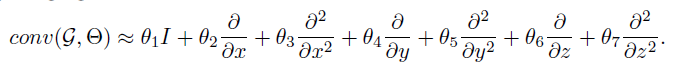
通过将投影的微分算子堆叠在每个轴上来定义图的梯度矩阵:

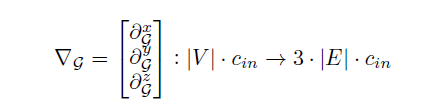
该梯度对于x，y，z方向,作用于顶点空间，其输出大小是图形边缘空间的3倍。为了将梯度收回顶点空间，作者使用了一个边缘平均算子：

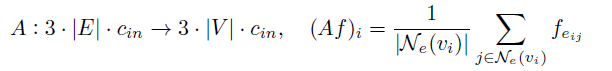
以类似的方式，可得相对于每个轴x，y，z的图拉普拉斯算子：

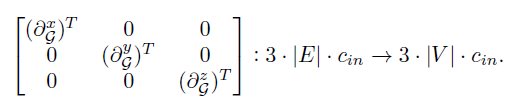
代数多重网格池化和解池化 作者使用AMG方法（Galerkin粗化），定义池运算符：

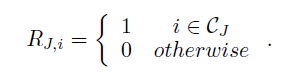
给定一个特征矩阵X和一个邻接矩阵A，通过Galerkin粗化定义它们的粗化对应项：

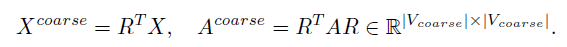
为了执行解池化运算和有一个更平滑的解池算子，作者通过池化运算符的转置和平滑聚合实现：

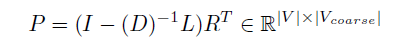
图1中显示了此工作中使用的体系结构：

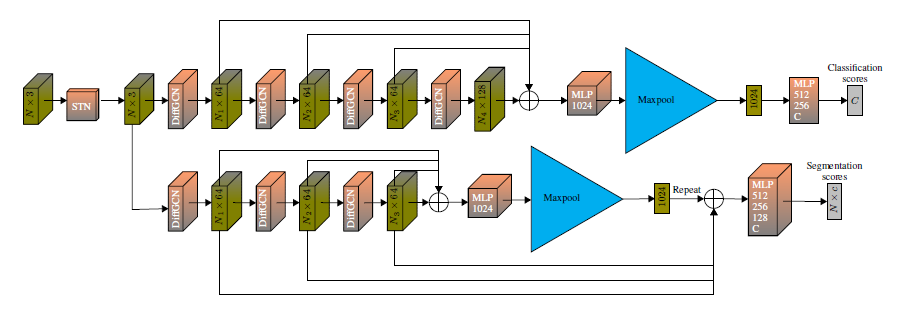
图1 DiffGCN 模型结构

实验

为了证明框架的有效性，作者在三个不同的数据集上进行了三个实验-分类（ModelNet40 ），部分分割（ShapeNet部件）和语义分割（S3DIS）。在所有实验中，实验数据都是从点云开始，并且在每个DiffGCN块中，根据点的特征构造一个K最近邻图。

分类结果 分类结果在所对比方法中效果最好，作者指出这种差异主要是由于拉普拉斯项加到卷积以及池化模块的贡献，结果如表1所示：

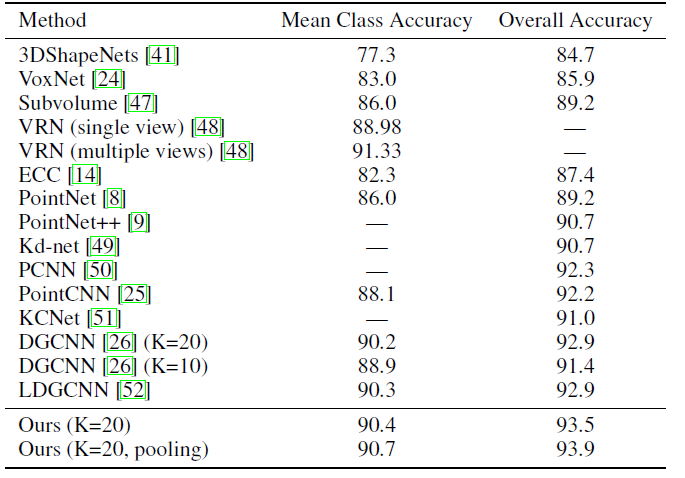
表1 分类结果

分割结果 作者在两个不同的分割数据集中测试了提出的方法，结果如表2，3所示，。在所有考虑的网络中，所提出的方法均实现了最高的mIoU：

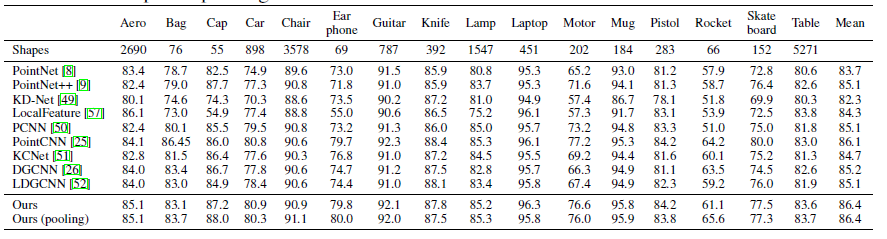
表2 ShapeNet分割结果

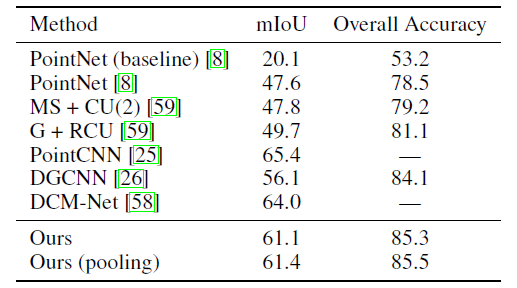
表3 S3DIS分割结果

总结

作者提出了一种基于离散差分算子的新颖图卷积核，它AMG池化和解池化运算符一起构成了CNN的最重要组成部分。与目前最先进的GCN相比，DiffGCN网络显示出同等或更好的性能。作者还对标准结构的CNN和所提出方法进行了类比，与其他GCN相比，成本有所降低。

参考资料

https://papers.nips.cc/paper/2020/file/d16a974d4d6d0d71b29bfbfe045f1da7-Paper.pdf