蓝桥杯《算法很美》第2章：递归
【摘要】 2.1递归与算法分析
练习1：求n的阶乘
求10的阶乘
解题思路：
!10 = 1x2x3x4x5...x10
答案如下：
public class Test08 {
public static void main(String[] args) {
System.out.println(f1(10));
}
/**
* 求x的阶乘
...
2.1递归与算法分析
练习1：求n的阶乘
求10的阶乘
解题思路：
!10 = 1x2x3x4x5...x10
答案如下：
public class Test08 {
public static void main(String[] args) {
System.out.println(f1(10));
}
/**
* 求x的阶乘
* * @param x
* @return
*/
static int f1(int x) {
if (x == 1) { return 1;
}
return x * f1(x - 1);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
练习2：打印i到j
打印从1到10，的十个数。
解题思路：
一般我们使用循环来打印，这里为了练习递归的使用，而采用递归的方式。
答案如下：
public class Test09 {
public static void main(String[] args) {
f2(1, 10);
} /**
* 打印从i到j
* @param i
* @param j
*/
static void f2(int i,int j) {
if (i==j) { System.out.println(i); return;
}
System.out.println(i);
f2(i+1, j);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
练习3：对数组元素求和
使用递归的方式对数组中的所有元素求和
解题思路：
一般我们通过遍历数组来进行求和，这里为了练习递归的使用，而采用递归的方式。
答案如下：
public class Test10 {
public static void main(String[] args) {
int[] arr = new int[] { 1, 2, 5, 9, 11, 15, 16 };
int result = f3(arr, 0);
System.out.println(result);
}
/**
* 求数组元素总和
* @param arr
* @param index
* @return
*/
static int f3(int[] arr, int index) {
if (index == arr.length - 1) { return arr[index];
}
return arr[index] + f3(arr, index + 1);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
练习4：翻转字符串
使用递归的方式反转字符串abcdef
解题思路：
略
答案如下：
public class Test11 {
public static void main(String[] args) {
String str = new String("abcdef");
String reverseStr = f4(str, str.length() - 1);
System.out.println(reverseStr);
}
/**
* 递归方式反转字符串
* @param str
* @param length
* @return
*/
static String f4(String str, int length) {
if (length == 0) { return "" + str.charAt(0);
}
return str.charAt(length) + f4(str, length - 1);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
练习5：斐波那契第n项
求斐波那契数列第n项
解题思路：
斐波那契数列：1，1，2，3，5，8，13，21…
即，除第1，2项外，所有当前项值为前两项值之和！
答案如下：
public class Test12 {
public static void main(String[] args) {
System.out.println(fib(8));
} /**
* 求斐波那契数列第n项的数值
* @param N
* @return
*/
static int fib(int N) {
if (N == 1|| N == 2) { return 1;
}
return fib(N-1) + fib(N-2);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
练习6：辗转相除求最大公因数
求2个数m，n(m>n)的最大公因数
解题思路：
- 若
m%n==0，则n是m和n的最大公因数。 - 若
m%n==k，则递归执行n%k==k2，k%k2==k3… 直到取余的结果为0，则被取余数kn就是 m和n的最大公因数！
答案如下：
public class Test13 {
public static void main(String[] args) {
System.out.println(f5(35, 12));
}
/**
* 求2个数的最大公因数
* @param m
* @param n
* @return
*/
static int f5(int m, int n) {
if (n == 0) { return m;
}
return f5(n, m % n);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
练习7：求最2个数的最小公倍数
求2个数m，n(m>n)的最小公倍数
解题思路：
- 最小公倍数，可以通过m和n的乘积除以二者的最大公约数，即可得到！
- 公式：
最小公倍数 = m* n / 最大公约数
答案如下：
public class Test13 {
public static void main(String[] args) {
// 最大公约数
System.out.println(f5(16, 12));
// 最小公倍数
System.out.println(16*12/f5(16, 12));
}
/**
* 求2个数的最大公因数
* @param m
* @param n
* @return
*/
static int f5(int m, int n) {
if (n == 0) { return m;
}
return f5(n, m % n);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
练习8：递归形式的插入排序
递归的方式实现插入排序
解题思路：
插入排序通过递归的方式实现。
答案如下：
public class Test14 {
public static void main(String[] args) {
int[] arr = new int[] { 1, 9, 8, 7, 11, 6, 44, 13 };
insertSort(arr, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
/**
* 递归方式实现插入排序
* * @param arr
* @param index
*/
static void insertSort(int[] arr, int index) {
if (index == 0) { return;
} // 先将index之前的排好序
insertSort(arr, index - 1); int value = arr[index];
int k = index - 1;
while (k > -1 && value < arr[k]) { arr[k + 1] = arr[k]; k--;
}
arr[k + 1] = value;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
练习9：汉诺塔问题
递归解决汉诺塔问题：将1~N从A移动到B，C作为辅助
解题思路：
- 先将1~N-1从A移动到C，B为辅助；
- 再把N从A移动到B；
- 然后1~N-1从C移动到B，A为辅助；
直接上图分析：
答案如下：
public class Test15 {
public static void main(String[] args) {
// 将汉诺塔从A移动到B,C作为辅助
HanoiTower(3,"A","B","C");
} /**
* 汉诺塔移动问题
* @param N
* @param from
* @param to
* @param help
*/
static void HanoiTower(int N,String from,String to,String help) {
if (N==1) { System.out.println("将"+N+"从"+from+"移动到"+to); return;
} HanoiTower(N-1,from,help,to);// 先将1~N-1从A移动到C，B为辅助；
System.out.println("将"+N+"从"+from+"移动到"+to);// 再把N从A移动到B；
HanoiTower(N-1,help,to,from);// 然后1~N-1从C移动到B，A为辅助；
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
练习10：二分查找递归解法
二分查找递归解法
解题思路：
分半查询！
答案如下：
public class Test16 {
public static void main(String[] args) {
int[] arr = new int[] { 1, 2, 3, 4, 10, 12, 14, 16, 19 }; int result = binarySearch(arr, 0, arr.length - 1, 10);
System.out.println("下标：" + result + " 值：" + arr[result]);
}
/**
* 递归实现二分查找
* @param arr
* @param low
* @param high
* @param key
* @return
*/
static int binarySearch(int[] arr, int low, int high, int key) {
if (low > high) { return -1;
}
int mid = low + ((high - low) >> 1);
int midVal = arr[mid]; if (key > midVal) { return binarySearch(arr, mid + 1, arr.length - 1, key);
} else if (key < midVal) { return binarySearch(arr, low, mid - 1, key);
} else { return mid;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
2.2算法复杂度和算法稳定性
算法时间复杂度
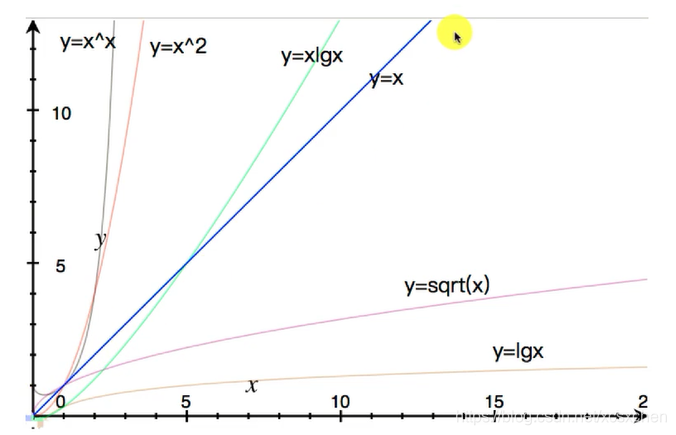
时间复杂度O表示案例
f(n) = 2n^2 + n +5 ---> O(n^2)
// O(n)
for(int i=1;i<=n;i++){} // O(n^2)
for(int i=1;i<=n;i++){ for(int i=1;i<=n;i++){}
} // O(n^2)
for(int i=1;i<=n;i++){ for(int j=1;j<=i;j++){}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
10种常见排序算法时间复杂度对比
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 |
| 希尔排序 | O(n^1.3) | O(n^2) | O(n) | O(1) | 不稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 |
| 冒泡排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 |
| 快速排序 | O(nlog2n) | O(n^2) | O(nlog2n) | O(nlog2n) | 不稳定 |
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | 稳定 |
| 桶排序 | O(n+k) | O(n^2) | O(n) | O(n+k) | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | 稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 |
2.3递归小节练习
第1题：小白上楼梯
小白正在上楼梯，楼梯有n阶台阶，小白一次可以上1阶，2阶或者3阶，实现一个方法，计算小白有多少种走完楼梯的方式。
提示：设n阶台阶的走法数为f(n)。如果只有1个台阶，走法有1种（一步上1个台阶），即f(1)=1；如果有2个台阶，走法有2种（一种是上1阶，再上1阶，另一种是一步上2阶），即f(2)=2；如果有3个台阶，走法有4种（一种每次1阶，共一种；另一种是2+1，共两种；第三种是3，共1种），即f(3)=4；
解题思路：
- 当只有1个台阶时只有1种走法；
- 当只有2个台阶时有2种走法；
- 当只有3个台阶时有4种走法；
- 当有n个台阶（n>3）时，我们缩小问题规模，可以这样想：最后一步有三种情况，走1阶（之前上了n-1个台阶，走法为f(n-1)种），走2阶（之前上了n-2个台阶，走法为f(n-2)种），走3阶，（之前上了n-3个台阶，走法为f(n-3)种，f(n)=f(n-1)+f(n-2)+f(n-3)，n>3；
代码如下：
public class Test17 {
public static void main(String[] args) {
int result = up(4);
System.out.println("总共有："+result+" 种走法");
}
/**
* 小白上楼梯
* * @param n
* @return
*/
static int up(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
if (n == 3) return 4;
return up(n - 1) + up(n - 2) + up(n - 3);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
第2题：设计一个高效的求a的n次幂的算法
设计一个高效的求a的n次幂的算法
解题思路：
略
代码如下：
static int pow(int a, int n) { if (n == 0) return 1; int res = a; int ex = 1; // 能翻 while ((ex << 1) <= n) { // 翻 res = res * res; // 指数 ex <<= 1; } // 不能翻 // 差n-ex次方没有去乘到结果里面 return res * pow(a, n - ex);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
文章来源: csp1999.blog.csdn.net，作者：兴趣使然の草帽路飞，版权归原作者所有，如需转载，请联系作者。
原文链接：csp1999.blog.csdn.net/article/details/114376849
【版权声明】本文为华为云社区用户转载文章，如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）