环形链表找入口,真的太妙了
链表是否有环问题看似简单,但实际处理上有很多需要注意的,这个问题是非常高频笔试面试题,记忆不牢固容易遗忘,可以认真看看学习一波!当然今天这两题对应力扣141和力扣142,有个小伙伴就在某手面试中遇到了。
判断链表是否有环
问题描述:
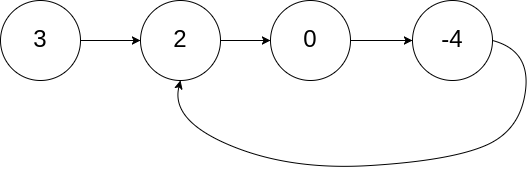
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。
如果链表中存在环,则返回 true 。否则,返回 false 。
你能用 O(1)(即,常量)内存解决此问题吗?
分析:
对于这个问题,如果没有内存空间的限制,首先想到的就是使用哈希的方法,用一个哈希存储节点,然后向下枚举链表节点:
如果发现其中有在哈希中,那么就说明有环返回true。
如果枚举到最后结束,那就说明没有环
但是这样并不满足O(1)空间复杂度的要求,我们应该怎么处理呢?
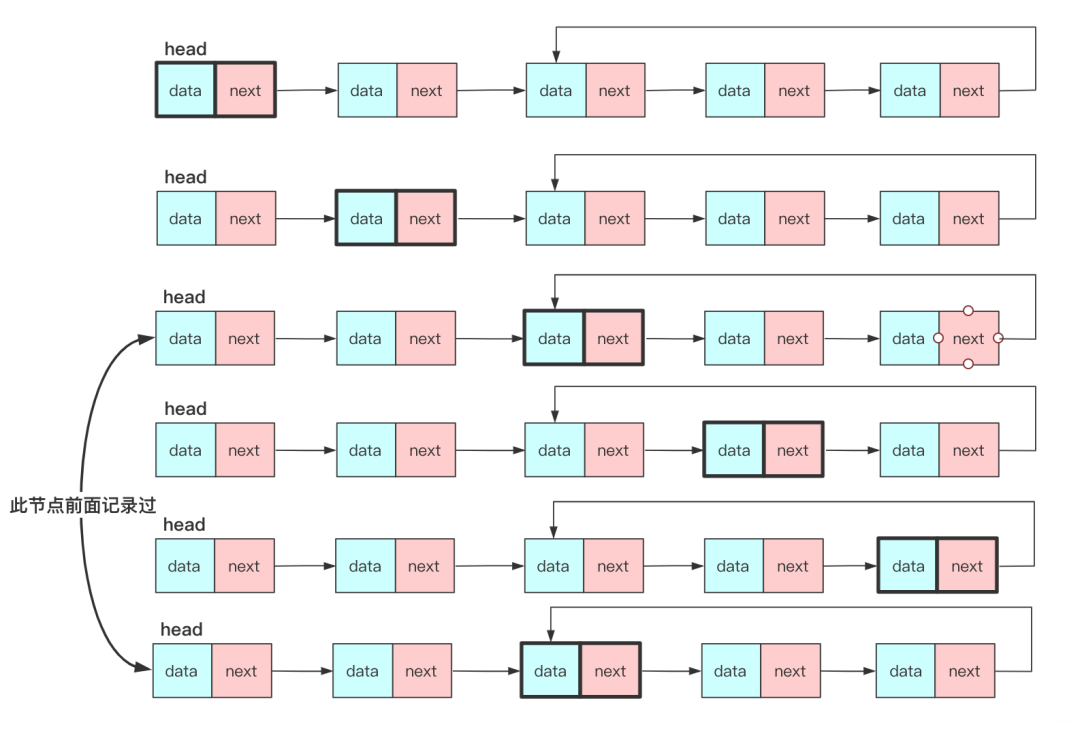
如果链表尾部有环,如果一个节点枚举到后面会在闭环中不断循环枚举,那么怎么样能高效判断有环并且能快速终止呢?
有环,其实就是第二次、第三次走过这条路才能说它有环,一个指针在不借助太多空间存储状态下无法有效判断是否有环(有可能链表很长、有可能已经在循环了),咱们可以借助 快慢指针(双指针) 啊。
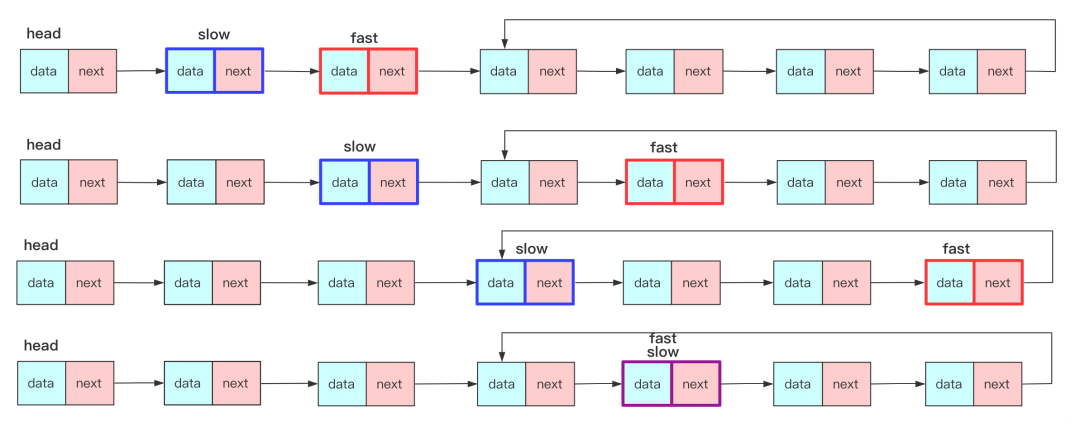
其核心思想就是利用两个指针:快指针(fast)和慢指针(slow),它们两个同时从链表头遍历链表,只不过两者速度不同,如果存在环那么最终会在循环链表中相遇。
我们在具体实现的时候,可以快指针(fast)每次走两步,慢指针(slow)每次走一步。如果存在环的话快指针先进入环,慢指针后入环,在慢指针到达末尾前快指针会追上慢指针。
快慢指针如果有相遇那就说明有环,如果快指针先为null那就说明没环。
具体实现代码为:
-
/**
-
* Definition for singly-linked list.
-
* class ListNode {
-
* int val;
-
* ListNode next;
-
* ListNode(int x) {
-
* val = x;
-
* next = null;
-
* }
-
* }
-
*/
-
public class Solution {
-
public boolean hasCycle(ListNode head) {
-
ListNode fast=head;
-
ListNode slow=fast;
-
while (fast!=null&&fast.next!=null) {
-
slow=slow.next;
-
fast=fast.next.next;
-
if(fast==slow)
-
return true;
-
}
-
return false;
-
}
-
}
提高:找到环的入口
给定一个链表,返回链表开始入环的第一个节点。如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
说明:不允许修改给定的链表。
你是否可以使用 O(1) 空间解决此题?
这题相比上一题又难了一些,因为如果链表成环,需要找到入口。
分析:
如果不考虑内存使用,我肯定还会首先考虑哈希,将节点存着然后如果出现第二次则说明有环并直接返回,实现的代码也很简单,走投无路可以用这个方法:
-
/**
-
* Definition for singly-linked list.
-
* class ListNode {
-
* int val;
-
* ListNode next;
-
* ListNode(int x) {
-
* val = x;
-
* next = null;
-
* }
-
* }
-
*/
-
public class Solution {
-
public ListNode detectCycle(ListNode head) {
-
int pos=-1;
-
Map<ListNode,Integer>map=new HashMap<ListNode, Integer>();
-
ListNode team=head;
-
while (team!=null)
-
{
-
if(map.containsKey(team)){
-
pos=map.get(team);
-
return team;
-
}
-
else
-
map.put(team,++pos);
-
team=team.next;
-
}
-
return null;
-
}
-
}
但是怎么使用O(1)的空间复杂度完成这个操作呢?上面一题的思路是使用快慢指针判断是否有环,但是怎么锁定环的入口呢?
这个题看起来是个算法题,实际上是个数学推理题。这题的关键也是快慢指针,不过需要挖掘更多的细节 。
回忆一下快慢指针能够挖掘的细节:
知道慢指针走了x步,快指针走了2x步,但是仅仅知道这两个条件还推导不出什么东西,我们能够进行的操作也只有用O(1)的方法进行一些操作。不过这里面快慢指针和前面有点不同的是我们前面用一个头结点开始计数。
我们还可以进行什么操作?
既然知道相遇的这个点在环内,那么我们可以用一个新的节点去枚举一圈看看环的长度是多少哇!
这里面,我们可以知道fast走的步数2x,slow走的步数x,以及环长y。
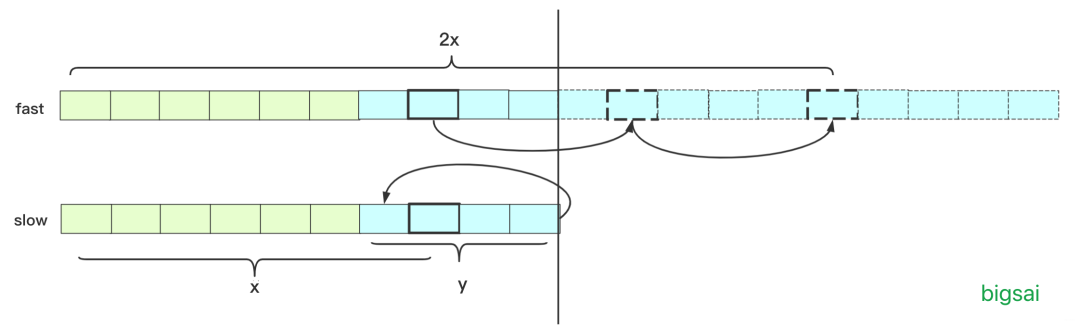
我们知道,慢指针是第一次入环,但快指针可能已经走了好几圈,但是多走的步数一定是环的整数倍(不然不可能在同一个位置相遇)。
那么可以得到 快指针步数=慢指针步数+n圈环长度。当然这里n我暂时不知道是多少。换算成公式,那就是 2x=x+ny 消去一个x得到:x=ny。
上面的图我也标注快指针多走的是整数圈数。难点就在这里,需要变通:
快指针多走的x是环长y的整数倍n,慢指针走的x也是环长y的整数倍n。
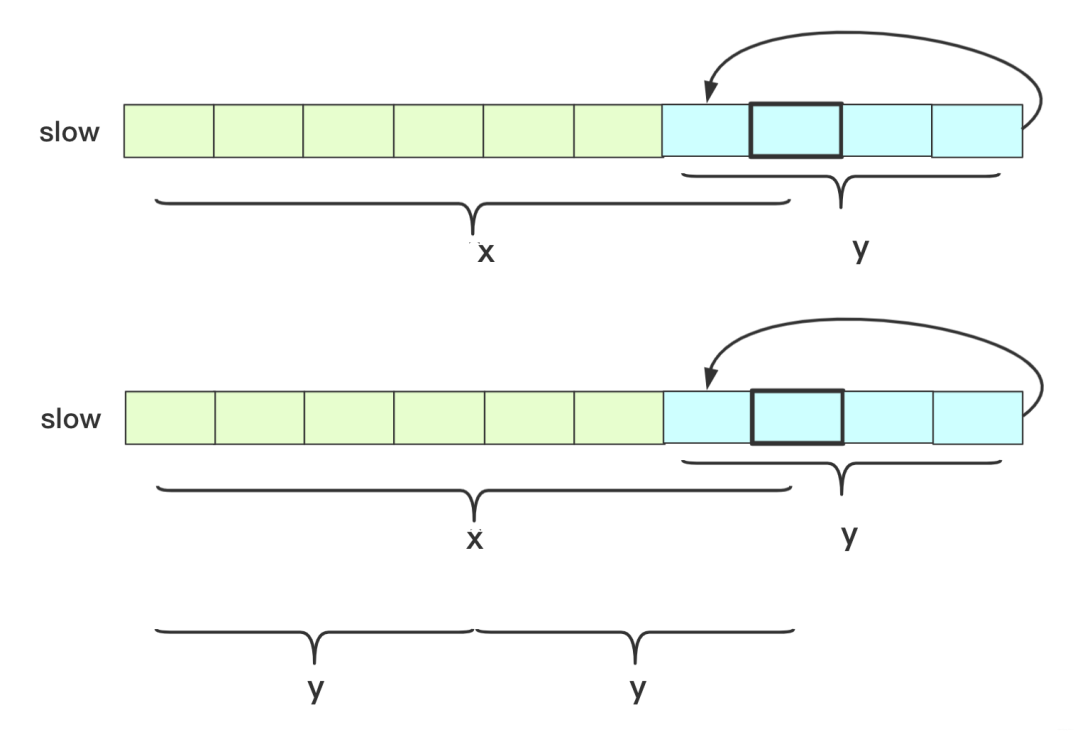
那么这样有什么用呢?
如果某个节点从起点出发,走到fast,slow交汇点走的是x步(n*y步)。此时,如果某个指针从fast,slow交汇点开始如果走环长的整数倍,那么它到时候还会在原位置。
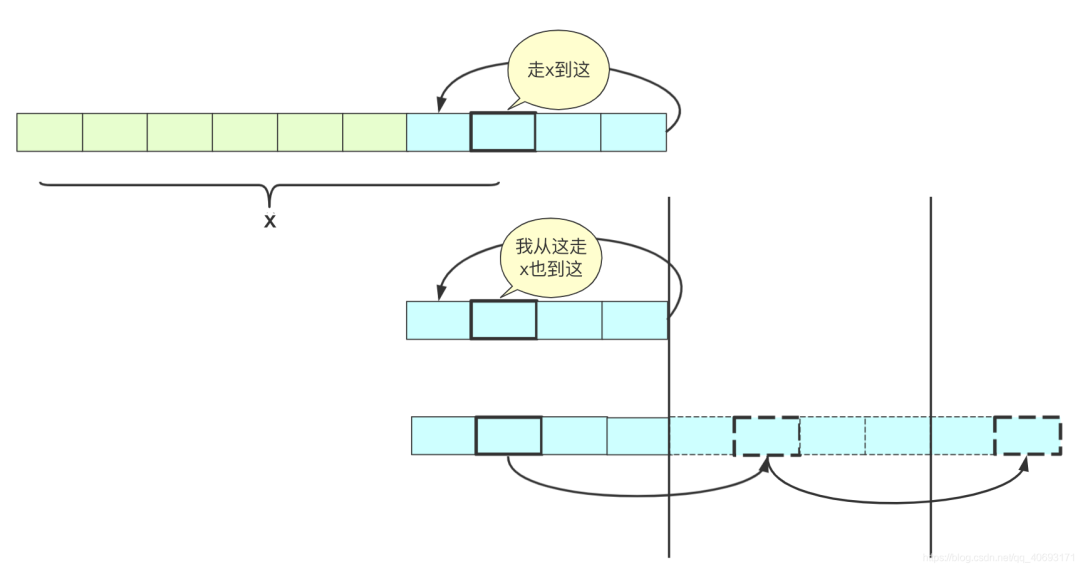
也就是说从开始head节点team1走x步,从fast,slow交汇节点team2走x步,它们最终依然到达fast,slow交汇的节点,但是在枚举的途中,一旦team1节点遍历的到环内,那么就和team2节点重合了,所以它们一旦相等那就是第一个交汇的点了。
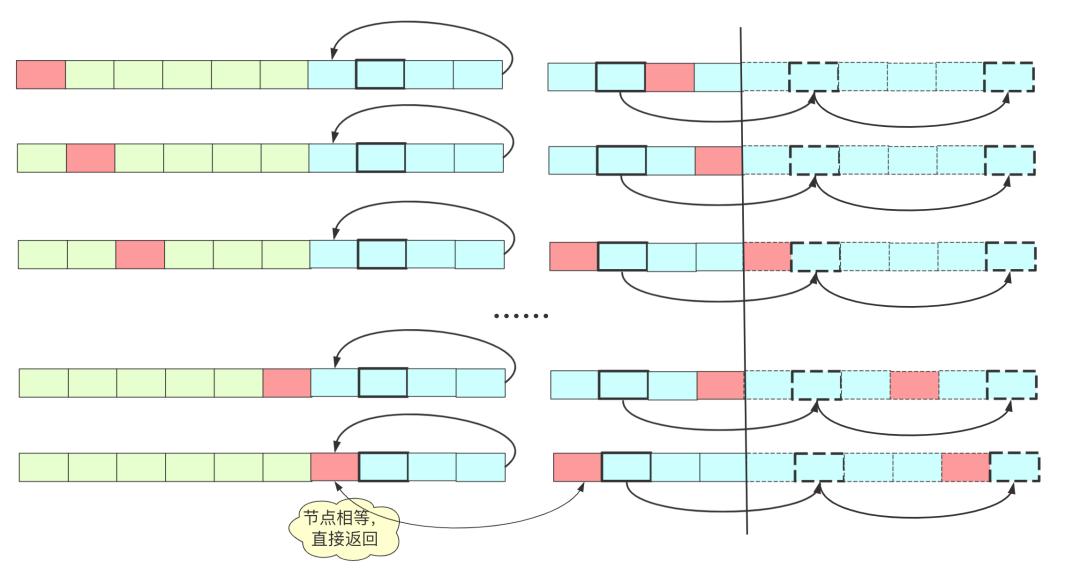
具体实现依然要判断是否有环,实现代码为:
-
/**
-
* Definition for singly-linked list.
-
* class ListNode {
-
* int val;
-
* ListNode next;
-
* ListNode(int x) {
-
* val = x;
-
* next = null;
-
* }
-
* }
-
*/
-
public class Solution {
-
public ListNode detectCycle(ListNode head) {
-
boolean isloop=false;
-
ListNode fast=new ListNode(0);//头指针
-
ListNode slow=fast;
-
fast.next=head;
-
if(fast.next==null||fast.next.next==null)
-
return null;
-
while (fast!=null&&fast.next!=null) {
-
fast=fast.next.next;
-
slow=slow.next;
-
if(fast==slow)
-
{
-
isloop=true;
-
break;
-
}
-
}
-
if(!isloop)//如果没有环返回
-
return null;
-
ListNode team=new ListNode(-1);//头指针 下一个才是head
-
team.next=head;
-
while (team!=fast) {
-
team=team.next;
-
fast=fast.next;
-
}
-
return team;
-
}
-
}
总结
到此,这个问题就介绍到这里,如果有想法欢迎留言,后面会继续分享更多数据结构与算法介绍以及重要题型,欢迎mark。
推荐阅读:

求个点赞在看你最好看
文章来源: bigsai.blog.csdn.net,作者:Big sai,版权归原作者所有,如需转载,请联系作者。
原文链接:bigsai.blog.csdn.net/article/details/117433307
- 点赞
- 收藏
- 关注作者


评论(0)