Day6、Python

题目 杨辉三角
1、程序分析
    杨辉三角基本性质：
    a、第n行的m个数可表示为 C(n-1,m-1)，即为从n-1个不同元素中取m-1个元素的组合数。
    b、每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
    举例：

    可以利用Python的生成器generator、sum、zip方法，来实现杨辉三角的打印。
2、程序实现

#Topic : 杨辉三角   
#File Name : Triangle.py
#Author : Jack Cui
#Created : 8 April 2016
def triangles(): a = [1] while True: yield a a = [sum(i) for i in zip([0] + a,a + [0])]

if __name__ == '__main__': h = int(input('请输入您要显示的最大行数：')) tri = triangles() for n in range(h): print(next(tri))

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
 

3、结果显示

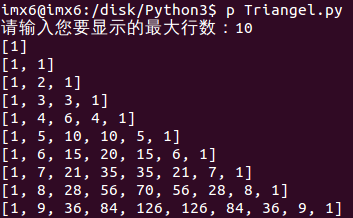
文章来源: jackcui.blog.csdn.net，作者：Jack-Cui，版权归原作者所有，如需转载，请联系作者。

原文链接：jackcui.blog.csdn.net/article/details/51094227