《算法导论》实验三:最佳调度问题的回溯算法
一、问题描述
设有n个任务由k个可并行工作的机器来完成,完成任务i需要时间为 。试设计一个算法找出完成这n个任务的最佳调度,使完成全部任务的时间最早。(要求给出调度方案)
- 1
二、算法设计与分析
1、算法核心思想
排列树回溯法+剪枝
2、解空间的表示
一个深度为N的K叉排列树。
3、基本思路
① 搜索从开始结点(根结点)出发,以DFS搜索整个解空间。每搜索完一条路径则记录下bestTime 和best_N_to_K []序列(用于构造最优解)。
② 开始结点就成为一个活结点,同时也成为当前的扩展结点。在当前的扩展结点处向纵深方向移至一个新结点,并成为一个新的活结点,也成为当前扩展结点。如果在当前的扩展结点处不能再向纵深方向扩展,则当前扩展结点就成为死结点。
③ 此时,应往回移动(回溯)至最近的一个活结点处,并使这个活结点成为当前的扩展结点;直至找到一个解或全部解。
三、结果与分析
(一)本实验的测试用例可通过系统调用随机函数随机生成。
输入:
N:任务数
K:机器数
输出:
1、原始任务时间对应表;
2、针对每个任务的最佳调度序列;
3、每台机器对应完成的任务。
(二)实验结果截图如下图-3:
A、情况一:任务数大于等于机器数,即N>=K,结果如下图-1,每个机器都分配有任务
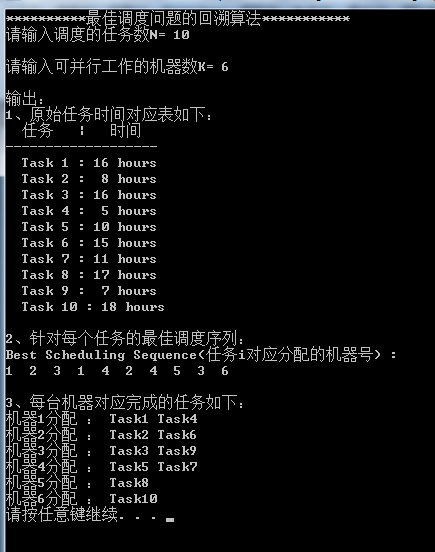
图-5 N>=K,每个机器都分配有任务
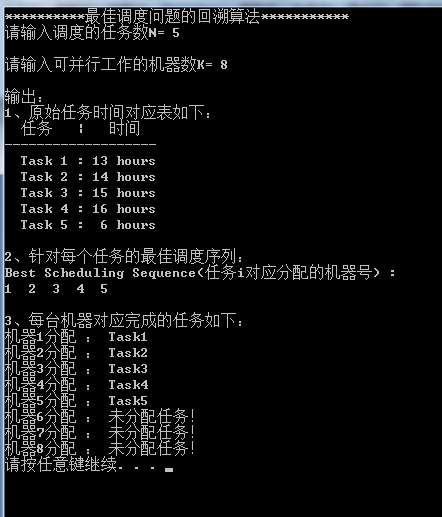
图-6 N< K,有未分配任务的机器
四、实验结论
1、 实验结果验证本算法可得到最优解:当任务数大于等于机器数,即N>=K,每个机器都分配有任务,也可能有未分配任务的机器,但不影响最终最优解值,因为最优解值可能有多个,而本实验只取其中一个;但当任务数小于机器数,即N< K,一定有未分配任务的机器。
2、 通过排列树回溯法的计算,可得到最优分配方案,但此问题的叶节点个数接近n!,遍历时间为Ω(n!),呈阶乘级增长,效率不是很高。例如在任务数N=20时,就需等待很长时间才能出结果。
3、 以DFS搜索解空间时,搜索过程中裁剪掉死结点的子树有利于提高搜索效率。本算法的剪枝约束条件为:ScheduleTime()< bestTime。
五、源代码(C++)
#include <iostream>
#include <ctime>
#include <random>
#include <iomanip>
#define INFINITY 999999999 //定义无穷大INFINITY=999999999
#define MAXSIZE 100 //定义最大任务数
using namespace std;
//定义所需全局变量
int N,K; //N:任务数,K:机器数
int taskTime[MAXSIZE]; //任务对应的时间
int bestTime=INFINITY; //最优解:即完成全部任务最短时间,初始化为无穷大
int scheduleNow[MAXSIZE]; //当前最优调度方案,值为0表示还未分配
int best_N_to_K[MAXSIZE]; //最优解的调度方案:best_N_to_K[i]=m,表示把i+1 //(i从0开始算)任务分配给第m台机器
//界面显示并接收N、K的值
void Display()
{ cout<<"**********最佳调度问题的回溯算法***********"<<endl; cout<<"请输入调度的任务数N= "; cin>>N; cout<<endl<<"请输入可并行工作的机器数K= "; cin>>K;
}
//随机产生完成任务i需要的时间
void setTaskTime(int taskTime[],int N)
{ srand(unsigned(time(NULL))); for(int i=0;i<N;i++) taskTime[i]=int((rand()%20)+3); //时间范围:[3,23)之间的整数
}
//打印原始任务时间对应表
void printTaskTime(int taskTime[],int N)
{ cout<<"\n输出:\n"<<"1、原始任务时间对应表如下:\n"<<" 任务 | 时间"<<endl<<"-------------------"<<endl; for(int i=0;i<N;i++) cout<<" Task "<<i+1<<" : "<<setw(2)<<taskTime[i]<<" hours"<<endl;
}
//搜索到叶节点时,计算叶节点可行解完成任务的时间
int ScheduleTime()
{ int k[MAXSIZE]={0}; //用于记录每个机器对应工作的总时间,机器下标 //从1开始算,因为scheduleNow[i]=0时表示未分配 for(int i=0;i<N;i++) {//将第i个任务时间加到第‘scheduleNow[i]’个机器中去 k[scheduleNow[i]]+=taskTime[i]; } int max=k[1]; for(int i=1;i<=K;i++) {//并行工作的所有机器中工作时间最长的那个时间就是叶子节点可行解时间 if(k[i]>max)max=k[i]; } return max;
}
//排列树回溯法(含剪枝)
void BackTrack(int deep)
{ if (deep==N) { int temp=ScheduleTime(); //临时存放叶节点的可行解的值 if(temp<bestTime) //可行解与当前最优解进行比较 { bestTime=temp; for(int i=0;i<N;i++) { best_N_to_K[i]=scheduleNow[i]; } } return; } for(int i=1;i<=K;i++) { scheduleNow[deep]=i; //将任务deep分配给当前机器 if(ScheduleTime()<bestTime) //剪枝,约束条件 BackTrack(deep+1); scheduleNow[deep]=0; //回溯,不将任务分配给当前机器,i=0表示为分配 }
}
//打印最终可行解结果
void printSchedulePlan()
{ //针对每个任务打印最佳调度序列 cout<<endl<<"2、针对每个任务的最佳调度序列:\n"; cout<<"Best Scheduling Sequence(任务i对应分配的机器号) :\n"; for(int i=0;i<N;i++) { cout<<best_N_to_K[i]<<" "; } //针对每台机器打印其对应完成那些任务 cout<<endl<<endl<<"3、每台机器对应完成的任务如下: \n"; for(int i=1;i<=K;i++) { bool hasTask=false; //hasTask用于记录机器是否有分配,若一 //个任务都没分配,则显示“未分配任务” cout<<"机器"<<i<<"分配 : "; for(int j=0;j<N;j++) { if(i==best_N_to_K[j]) { cout<<"Task"<<j+1<<" "; hasTask=true; } } if(hasTask==false)cout<<"未分配任务!"; cout<<endl; }
}
int main()
{ Display(); //界面显示并接收N、K setTaskTime(taskTime,N); //随机产生完成任务i需要的时间 printTaskTime(taskTime,N); //打印原始任务时间对应表 BackTrack(0); //排列树回溯法(含剪枝) printSchedulePlan(); //打印最终可行解结果 system("pause");
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
文章来源: blog.csdn.net,作者:allinallinallin,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/to_Baidu/article/details/50294231
- 点赞
- 收藏
- 关注作者


评论(0)