HDOJ 1081（ZOJ 1074） To The Max（动态规划）

Problem Description
Given a two-dimensional array of positive and negative integers, a sub-rectangle is any contiguous sub-array of size 1 x 1 or greater located within the whole array. The sum of a rectangle is the sum of all the elements in that rectangle. In this problem the sub-rectangle with the largest sum is referred to as the maximal sub-rectangle.

As an example, the maximal sub-rectangle of the array:

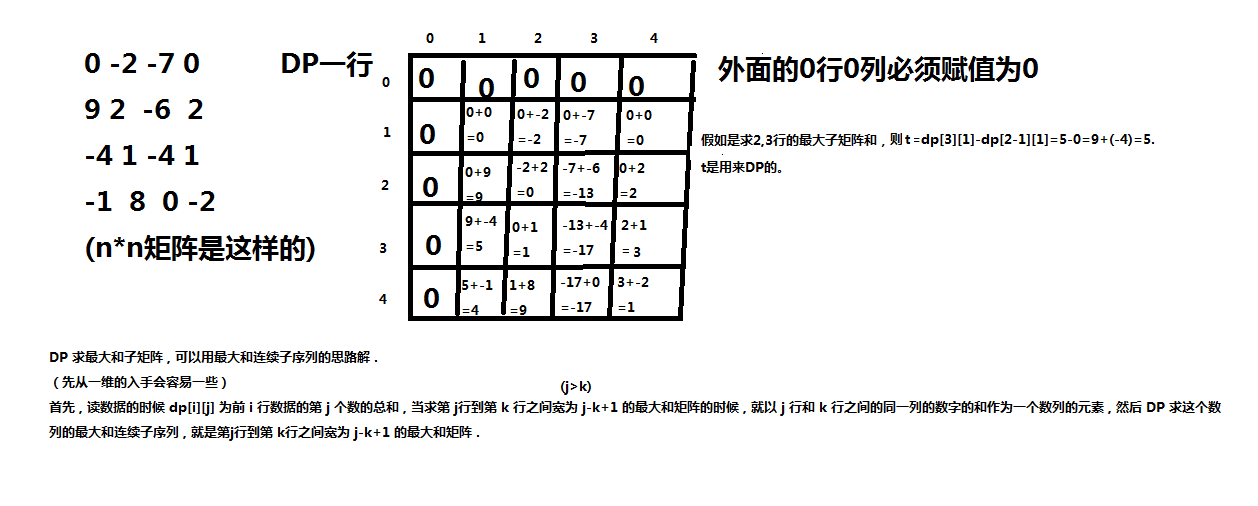
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

is in the lower left corner:

9 2
-4 1
-1 8

and has a sum of 15.

Input
The input consists of an N x N array of integers. The input begins with a single positive integer N on a line by itself, indicating the size of the square two-dimensional array. This is followed by N 2 integers separated by whitespace (spaces and newlines). These are the N 2 integers of the array, presented in row-major order. That is, all numbers in the first row, left to right, then all numbers in the second row, left to right, etc. N may be as large as 100. The numbers in the array will be in the range [-127,127].

Output
Output the sum of the maximal sub-rectangle.

Sample Input
4
0 -2 -7 0 9 2 -6 2
-4 1 -4 1 -1
8 0 -2

Sample Output
15

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int a[2000];
int dp[150][150];

int main(){ int n; while(scanf("%d",&n)==1){ int t; memset(dp,0,sizeof(dp)); for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ scanf("%d",&t); dp[i][j]=t+dp[i-1][j]; /// printf("i=%d",i); } }
// for(int i=0;i<=n;i++){
// for(int j=0;j<=n;j++){
// printf("%4d",dp[i][j]);
// }
// printf("\n");
// } int maxx=-1000; for(int i=1;i<=n;i++){ for(int j=i;j<=n;j++){ int sum=0; for(int k=1;k<=n;k++){ t=dp[j][k]-dp[i-1][k]; sum+=t; if(sum<0)  sum=0; if(sum>maxx) maxx=sum; } } } printf("%d\n",maxx); } return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
 

文章来源: chenhx.blog.csdn.net，作者：谙忆，版权归原作者所有，如需转载，请联系作者。

原文链接：chenhx.blog.csdn.net/article/details/49700861