神经网络的参数

导言

在上一篇神经网络的介绍当中，具体说明了一个神经元到整个神经网络的形式介绍，但其实并未说明完整；主要完成了神经网络对于“主动性”地一层层接受输入与输出结果，但并未说明其中的参数该如何进行确定的问题，这里将从实际运用的方面进行进一步的探讨。

参数形成

对于神经网络的参数，第一项主要的任务就是需要知道每一层所需的参数shape大小，这里通过图片的形式进行说明。

从这一简单的两层神经网络（输入层不算）开始说明。（为了节省计算成本，所有的神经网络的计算都是通过向量乘积的方式进行！而我使用Python进行代码书写）

由于输入x的shape大小为（2，1），而所运用到的式子为：Z=np.dot(W,X)+b，所以规定了W的参数shape大小格式为（n_h,n_x），其中n_x为x输入的个数为2，n_h为本层的神经元个数，也为2，所以第一层神经网络的shape大小为（2，2），而b的shape为（n_h,1）,即（2，1）。（之后读者可以尝试想想第二层也就是Z^2的参数W、b的shape大小）
知道shape大小之后，便是初始化。这里我使用的如下代码进行初始化：

W = np.random.randn(n_h,n_x)*0.1
b = np.random.zeros((n_h,1))

这时就会有人会看到，都是使用random的方法，凭什么W用randn方法随机产生(n_h,n_x)的数字，而b却要用zeros产生所有都是0的数字呢？

首先，我们就要看原来的神经网络的结构了，如果所有的W（W1、W2……）都是用一种相同shape、数值大小的矩阵去初始化，那么在之后进行相同的输入值，相同的计算形式，所得到的值肯定是会一样的，那么就失去了多个神经元在同一层去进行参数设置的必要性，而若W之间的参数值不一样，那么就算是b的参数值为0，那么同一层的神经元也能体现出不同的效果了，对于参数的训练过程，其效果就没那么明显。

（这时杠精就要来了！）

那我让W用zeros来初始化，然后b用randn方法初始化也行呀！

嗯，我只能说，你说的有道理，但效率上还是不如randn去初始化，因为b的shape大小小于W的，所以给W进行randn初始化明显更加有效果。（至于都用randn初始化的想法，结合上面的想想，就知道这样不一定是锦上添花，而是画蛇添足）

当然这些杠精方法并不是不能出结果，而只是效率上小于或略小于我所写的初始化方法而已。

参数的训练

介绍完参数的形成，就到了训练的过程——因为初始化得到的结果不可能直接使用在我们所需要的模型上。

梯度下降

提出这个概念，这个算法是主要完成参数的训练，有以下模块。

1. 损失函数

定义损失函数的作用主要看我进行参数训练的过程中，我参数形成的模型对于结果的得出效果如何。
基础函数LOSS FUNCTION：

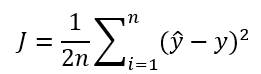
这个较为容易就能看出计算yhat与y之间的差距的函数，即为损失函数，可以较好的判断此时计算出的yhat值对于实际结果y的差距。

j = 1/n* np.sum((np.expand_dims(Y,1)-S)**2)

如何缩减这个函数的大小值，就涉及到多元二次函数的求偏导问题。

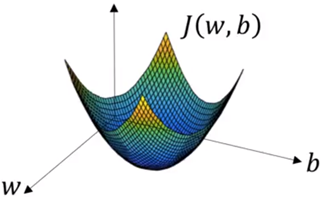
从这个图像中较为清晰的感受到，如果我的W、b的取值能不断地趋近于J大小的底部时，那么说明损失值越小。那么就是通过求偏导、更新参数值地过程实现。

2. 求偏导

这个属于高数的范围，我就简单举例计算，展示过程即可（链式法则很重要！）

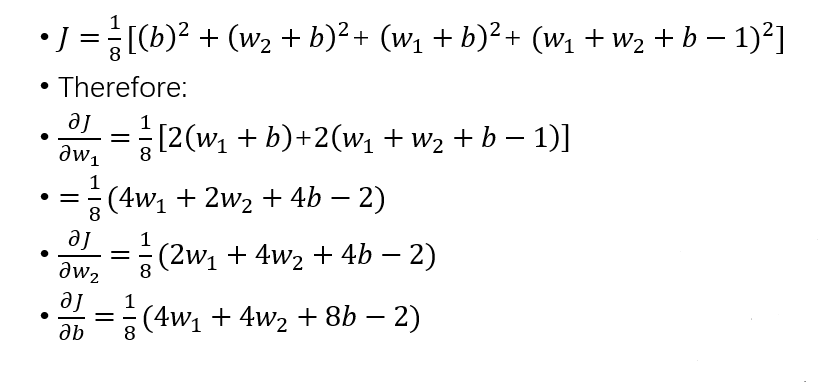
3. 更新参数

如何更新参数，我将以偏导后的函数值进行训练参数，偏导后，三维的函数图像，可以降维为二维进行说明。

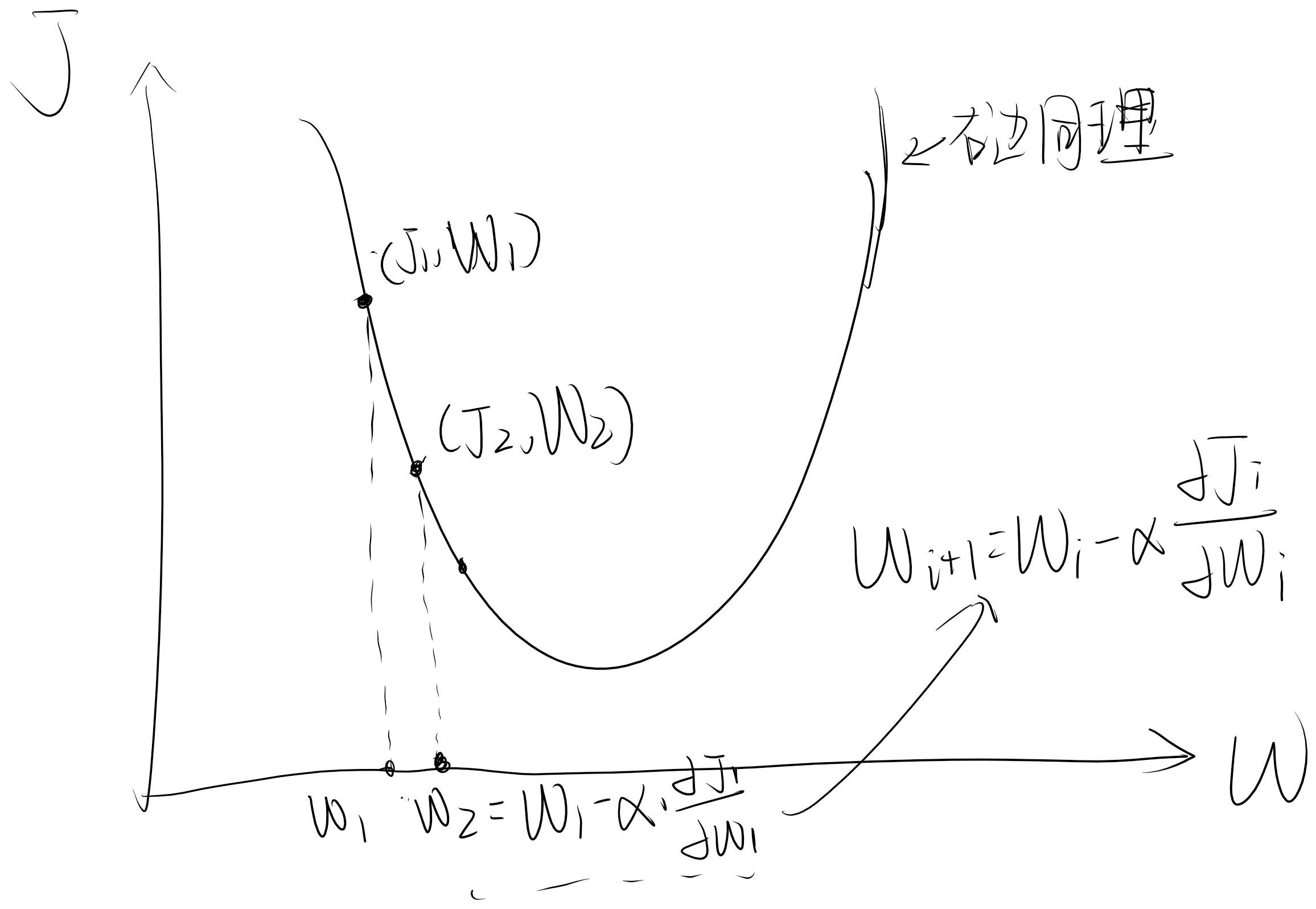
以上是说明如下公式的运用：

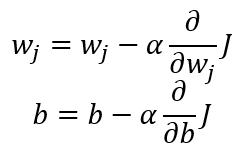
W = W - α*G

其中，α为学习率，即每次更新参数的幅度设置，一般设计为较小值（例：α=0.001）G为所求的偏导函数值！
为此进行计算后，参数取值后，J所对应的值都会沿着弧线下降的过程，即表现为梯度下降的过程。

以上训练的过程又统称为向后传播(Back Propagation)

另一损失函数

之前基础的损失函数在无激活函数的线性神经网络的情况下还好，但加入激活函数后所得到的结果变得不那么理想。
（图片）
为此进一步提出更加适合有激活函数条件下的损失函数:

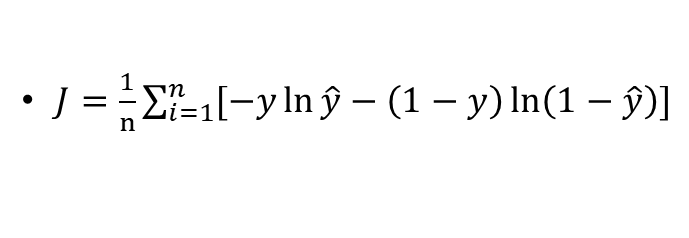
G = np.dot(X.T, 1 / n * (np.expand_dims(Y, 1) - S) * (-1) * S * (1 - S))

本损失函数的使用说明，在往后的文章中再作解释，这里不多做赘述。
依然是求偏导（链式法则）、更新参数。（以下举个偏导例子）

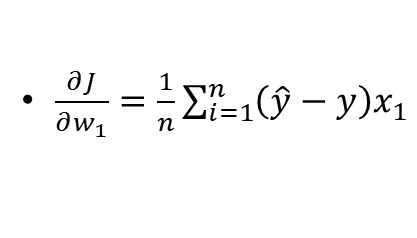
实际的全过程分为前向传播和后向传播两大部分，全过程举例展示如下：

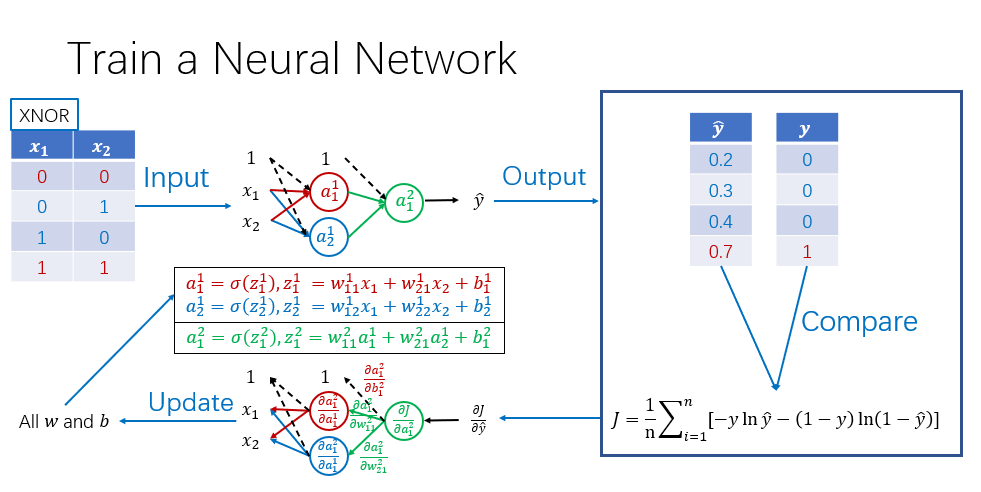
结言

以上就是神经网络的参数形成和训练的全部内容，如果对你有帮助，请点个赞，还想了解后续更新，就点亮关注，或者再评论区提出你的疑问，谢谢!