斐波那契之美

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”。

这个数列就是1、1、2、3、5、8、13、21、34、……

在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

但是斐波那契的知识不止于此，它还有很多惊艳到我的地方，下面我们就一起了解一下：

1. 随着数列项数的增加，前一项与后一项之比越来越逼近黄金分割的数值0.6180339887..
2. 从第二项开始，每个奇数项的平方都比前后两项之积多1，每个偶数项的平方都比前后两项之积少1。（注：奇数项和偶数项是指项数的奇偶，而并不是指数列的数字本身的奇偶，比如第五项的平方比前后两项之积多1，第四项的平方比前后两项之积少1）
3. 斐波那契数列的第n项同时也代表了集合{1,2,…,n}中所有不包含相邻正整数的子集个数。
4. f(0)+f(1)+f(2)+…+f(n)=f(n+2)-1
5. f(1)+f(3)+f(5)+…+f(2n-1)=f(2n)
6. f(2)+f(4)+f(6)+…+f(2n) =f(2n+1)-1
7. [f(0)]^2+[f(1)]^2+…+[f(n)]^2=f(n)·f(n+1)
8. f(0)-f(1)+f(2)-…+(-1)^n·f(n)=(-1)^n·[f(n+1)-f(n)]+1
9. f(m+n)=f(m-1)·f(n-1)+f(m)·f(n) (利用这一点，可以用程序编出时间复杂度仅为O（log n）的程序。)

真的不禁感叹：真是一个神奇的数列啊

桶排序

我们都知道，基于比较的排序，时间的极限就是O(NlogN)，从来没有哪个排序可以突破这个界限，如速度最快的快速排序，想法新颖的堆排序，分治的归并排序。

但是，如果我们的排序根本就不基于比较，那就可能突破这个时间。

桶排序不是基于比较的排序方法，只需对号入座。将相应的数字放进相应编号的桶即可。

当要被排序的数组内的数值是均匀分配的时候，桶排序使用线性时间o（n）

对于海量有范围数据十分适合，比如全国高考成绩排序，公司年龄排序等等。

  

   

    

     

    
    

     

      l=list(map(int,input().split(" ")))
     
    
   

    

     

    
    

     

      n=max(l)-min(l)
     
    
   

    

     

    
    

     

      p=[0]*(n+1)#为了省空间
     
    
   

    

     

    
    

     

      for i in l:
     
    
   

    

     

    
    

     

       p[i-min(l)]=1#去重排序，做标记即可
     
    
   

    

     

    
    

     

      for i in range(n):
     
    
   

    

     

    
    

     
 if p[i]==1:#判断是否出现过
     
    
   

    

     

    
    

     

       print(i+min(l),end=" ")
     
    
  
 

当然，基数排序是桶排序的改良版，也是非常好的排序方法，具体操作是：把数字的每一位都按桶排序排一次，因为桶排序是稳定的排序，因此从个位进行桶排序，然后十位进行桶排序。。。直到最高位，排序结束。

这样极大的弱化了桶排序范围有限的弱点，比如范围1-100000需要准备100000个铜，而基数排序只要10个铜就够了（因为一共就十个数字。）。

想出这个排序的人也是个天才啊。。。选择合适的场合使用觉得有很好的效果。

快速排序

快速排序（Quicksort）是对冒泡排序的一种改进。

快速排序由C. A. R. Hoare在1962年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
分三区优化1：

在使用partition-exchange排序算法时，如快速排序算法，我们会遇到一些问题，比如重复元素太多，降低了效率，在每次递归中，左边部分是空的(没有元素比关键元素小)，而右边部分只能一个一个递减移动。结果导致耗费了二次方时间来排序相等元素。这时我们可以多分一个区，即，小于区，等于区，大于区。（传统快排为小于区和大于区）

下面我们通过一个经典例题来练习这种思想。

荷兰国旗问题

”荷兰国旗难题“是计算机科学中的一个程序难题，它是由Edsger Dijkstra提出的。荷兰国旗是由红、白、蓝三色组成的。

现在有若干个红、白、蓝三种颜色的球随机排列成一条直线。现在我们的任务是把这些球按照红、白、蓝排序。

样例输入

3
BBRRWBWRRR
RRRWWRWRB
RBRW
样例输出

RRRRRWWBBB
RRRRRWWWB
RRWB
思路：

现在我们的思路就是把未排序时前部和后部分别排在数组的前面和后面，那么中部自然就排好了。

设置两个标志位head指向数组开头，tail指向数组末尾，now从头开始遍历：

(1)如果遍历到的位置为1，那么它一定是属于前部，于是就和head交换值，然后head++，now++；

(2)如果遍历到的位置为2，说明属于中部，now++；

(3)如果遍历到的位置为3，说明属于后部，于是就和tail交换值，然而，如果此时交换后now指向的值属于前部，那么就执行(1)，tail--；

废话不多说，上代码。

  

   

    

     

    
    

     

      #include<iostream>
     
    
   

    

     

    
    

     

      #include<algorithm>
     
    
   

    

     

    
    

     

      using namespace std;
     
    
   

    

     

    
    

     

       
     
    
   

    

     

    
    

     

      const int maxn = 100 + 5;
     
    
   

    

     

    
    

     

       
     
    
   

    

     

    
    

     

      int n;
     
    
   

    

     

    
    

     

      string str;
     
    
   

    

     

    
    

     

      int main(){
     
    
   

    

     

    
    

     

          cin>>n;
     
    
   

    

     

    
    

     

          while(n--){
     
    
   

    

     

    
    

     

              cin>>str;
     
    
   

    

     

    
    

     

              int len=str.size();
     
    
   

    

     

    
    

     

              int now=0,ans=0;
     
    
   

    

     

    
    

     

              int head=0,tail=len-1;
     
    
   

    

     

    
    

     

              while(now<=tail){
     
    
   

    

     

    
    

     

                  if(str[now]=='R'){
     
    
   

    

     

    
    

     

                      swap(str[head],str[now]);
     
    
   

    

     

    
    

     

                      head++;
     
    
   

    

     

    
    

     

                      now++;
     
    
   

    

     

    
    

     

                  }
     
    
   

    

     

    
    

     

                  else if(str[now]=='W'){
     
    
   

    

     

    
    

     

                      now++;
     
    
   

    

     

    
    

     

                  }
     
    
   

    

     

    
    

     

                  else{
     
    
   

    

     

    
    

     

                      swap(str[now],str[tail]);
     
    
   

    

     

    
    

     

                      tail--;
     
    
   

    

     

    
    

     

                  }
     
    
   

    

     

    
    

     

              }
     
    
   

    

     

    
    

     

              cout<<str<<endl;
     
    
   

    

     

    
    

     

          }return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

快排分三区以后降低了递归规模，避免了最差情况，性能得到改进。
但是还是存在退化情况：

随机化快排优化2：
快速排序的最坏情况基于每次划分对主元的选择。基本的快速排序选取第一个元素作为主元。这样在数组已经有序的情况下，每次划分将得到最坏的结果。比如1 2 3 4 5，每次取第一个元素，就退化为了O(N^2)。一种比较常见的优化方法是随机化算法，即随机选取一个元素作为主元。

这种情况下虽然最坏情况仍然是O(n^2)，但最坏情况不再依赖于输入数据，而是由于随机函数取值不佳。实际上，随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度。
 

  

   

    

     

    
    

     

      def gg(a,b):
     
    
   

    

     

    
    

     
 global l
     
    
   

    

     

    
    

     
 if a>=b:#注意停止条件，我以前没加>卡了半小时
     
    
   

    

     

    
    

     
 return
     
    
   

    

     

    
    

     

       x,y=a,b
     
    
   

    

     

    
    

     
 import random#为了避免遇到基本有序序列退化，随机选点
     
    
   

    

     

    
    

     

       g=random.randint(a,b)
     
    
   

    

     

    
    

     

       l[g],l[y]=l[y],l[g]#交换选中元素和末尾元素
     
    
   

    

     

    
    

     
 while a<b:
     
    
   

    

     

    
    

     
 if l[a]>l[y]:#比目标元素大
     
    
   

    

     

    
    

     

       l[a],l[b-1]=l[b-1],l[a]#交换
     
    
   

    

     

    
    

     

       b=b-1#大于区扩大
     
    
   

    

     

    
    

     
 #注意：换过以后a不要加，因为新换过来的元素并没有判断过
     
    
   

    

     

    
    

     
 else:a=a+1#小于区扩大
     
    
   

    

     

    
    

     

       l[y],l[a]=l[a],l[y]#这时a=b
     
    
   

    

     

    
    

     
 #现在解释a和b：a的意义是小于区下一个元素
     
    
   

    

     

    
    

     
 #b是大于区的第一个元素
     
    
   

    

     

    
    

     

       gg(x,a-1)#左右分别递归
     
    
   

    

     

    
    

     

       gg(a+1,y)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      l=list(map(int,input().split(" ")))
     
    
   

    

     

    
    

     

      gg(0,len(l)-1)
     
    
   

    

     

    
    

     

      print(l)
     
    
  
 

BFPRT

我们以前写过快排的改进求前k大或前k小，但是快排不可避免地存在退化问题，即使我们用了随机数等优化，最差情况不可避免的退化到了O(N^2），而BFPRT就解决了这个问题，主要的思想精华就是怎么选取划分值。

我们知道，经典快排是选第一个数进行划分。而改进快排是随机选取一个数进行划分，从概率上避免了基本有序情况的退化。而BFPRT算法选划分值的规则比较特殊，保证了递归最小的缩减规模也会比较大，而不是每次缩小一个数。

这个划分值如何划分就是重点。

如何让选取的点无论如何都不会太差。

1、将n个元素划分为n/5个组，每组5个元素
2、对每组排序，找到n/5个组中每一组的中位数； 
3、对于找到的所有中位数，调用BFPRT算法求出它们的中位数，作为划分值。

下面说明为什么这样找划分值。

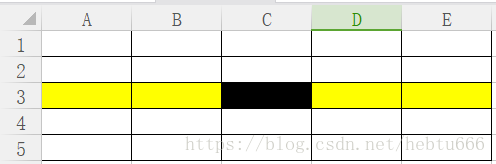
我们先把数每五个分为一组。

同一列为一组。

排序之后，第三行就是各组的中位数。

我们把第三行的数构成一个数列，递归找，找到中位数。

这个黑色框为什么找的很好。

因为他一定比A3、B3大，而A3、B3、C3又在自己的组内比两个数要大。

我们看最差情况：求算其它的数都比c3大，我们也能在25个数中缩小九个数的规模。大约3/10.

我们就做到了最差情况固定递减规模，而不是可能缩小的很少。

下面代码实现：

  

   

    

     

    
    

     

      public class BFPRT {
     
    
   

    

     

    
    

     

      //前k小
     
    
   

    

     

    
    

     
	public static int[] getMinKNumsByBFPRT(int[] arr, int k) {
     
    
   

    

     

    
    

     
		if (k < 1 || k > arr.length) {
     
    
   

    

     

    
    

     
			return arr;
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     
		int minKth = getMinKthByBFPRT(arr, k);
     
    
   

    

     

    
    

     
		int[] res = new int[k];
     
    
   

    

     

    
    

     
		int index = 0;
     
    
   

    

     

    
    

     
		for (int i = 0; i != arr.length; i++) {
     
    
   

    

     

    
    

     
			if (arr[i] < minKth) {
     
    
   

    

     

    
    

     

       res[index++] = arr[i];
     
    
   

    

     

    
    

     

      			}
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     
		for (; index != res.length; index++) {
     
    
   

    

     

    
    

     

      			res[index] = minKth;
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     
		return res;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      //第k小
     
    
   

    

     

    
    

     
	public static int getMinKthByBFPRT(int[] arr, int K) {
     
    
   

    

     

    
    

     
		int[] copyArr = copyArray(arr);
     
    
   

    

     

    
    

     
		return select(copyArr, 0, copyArr.length - 1, K - 1);
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
	public static int[] copyArray(int[] arr) {
     
    
   

    

     

    
    

     
		int[] res = new int[arr.length];
     
    
   

    

     

    
    

     
		for (int i = 0; i != res.length; i++) {
     
    
   

    

     

    
    

     

      			res[i] = arr[i];
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     
		return res;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      //给定一个数组和范围，求第i小的数
     
    
   

    

     

    
    

     
	public static int select(int[] arr, int begin, int end, int i) {
     
    
   

    

     

    
    

     
		if (begin == end) {
     
    
   

    

     

    
    

     
			return arr[begin];
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     
		int pivot = medianOfMedians(arr, begin, end);//划分值
     
    
   

    

     

    
    

     
		int[] pivotRange = partition(arr, begin, end, pivot);
     
    
   

    

     

    
    

     
		if (i >= pivotRange[0] && i <= pivotRange[1]) {
     
    
   

    

     

    
    

     
			return arr[i];
     
    
   

    

     

    
    

     

      		} else if (i < pivotRange[0]) {
     
    
   

    

     

    
    

     
			return select(arr, begin, pivotRange[0] - 1, i);
     
    
   

    

     

    
    

     

      		} else {
     
    
   

    

     

    
    

     
			return select(arr, pivotRange[1] + 1, end, i);
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      //在begin end范围内进行操作
     
    
   

    

     

    
    

     
	public static int medianOfMedians(int[] arr, int begin, int end) {
     
    
   

    

     

    
    

     
		int num = end - begin + 1;
     
    
   

    

     

    
    

     
		int offset = num % 5 == 0 ? 0 : 1;//最后一组的情况
     
    
   

    

     

    
    

     
		int[] mArr = new int[num / 5 + offset];//中位数组成的数组
     
    
   

    

     

    
    

     
		for (int i = 0; i < mArr.length; i++) {
     
    
   

    

     

    
    

     
			int beginI = begin + i * 5;
     
    
   

    

     

    
    

     
			int endI = beginI + 4;
     
    
   

    

     

    
    

     

      			mArr[i] = getMedian(arr, beginI, Math.min(end, endI));
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     
		return select(mArr, 0, mArr.length - 1, mArr.length / 2);
     
    
   

    

     

    
    

     
 //只不过i等于长度一半，用来求中位数
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      //经典partition过程
     
    
   

    

     

    
    

     
	public static int[] partition(int[] arr, int begin, int end, int pivotValue) {
     
    
   

    

     

    
    

     
		int small = begin - 1;
     
    
   

    

     

    
    

     
		int cur = begin;
     
    
   

    

     

    
    

     
		int big = end + 1;
     
    
   

    

     

    
    

     
		while (cur != big) {
     
    
   

    

     

    
    

     
			if (arr[cur] < pivotValue) {
     
    
   

    

     

    
    

     

       swap(arr, ++small, cur++);
     
    
   

    

     

    
    

     

      			} else if (arr[cur] > pivotValue) {
     
    
   

    

     

    
    

     

       swap(arr, cur, --big);
     
    
   

    

     

    
    

     

      			} else {
     
    
   

    

     

    
    

     

       cur++;
     
    
   

    

     

    
    

     

      			}
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     
		int[] range = new int[2];
     
    
   

    

     

    
    

     

      		range[0] = small + 1;
     
    
   

    

     

    
    

     

      		range[1] = big - 1;
     
    
   

    

     

    
    

     
		return range;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      //五个数排序，返回中位数
     
    
   

    

     

    
    

     
	public static int getMedian(int[] arr, int begin, int end) {
     
    
   

    

     

    
    

     

      		insertionSort(arr, begin, end);
     
    
   

    

     

    
    

     
		int sum = end + begin;
     
    
   

    

     

    
    

     
		int mid = (sum / 2) + (sum % 2);
     
    
   

    

     

    
    

     
		return arr[mid];
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      //手写排序
     
    
   

    

     

    
    

     
	public static void insertionSort(int[] arr, int begin, int end) {
     
    
   

    

     

    
    

     
		for (int i = begin + 1; i != end + 1; i++) {
     
    
   

    

     

    
    

     
			for (int j = i; j != begin; j--) {
     
    
   

    

     

    
    

     
 if (arr[j - 1] > arr[j]) {
     
    
   

    

     

    
    

     

       swap(arr, j - 1, j);
     
    
   

    

     

    
    

     

       } else {
     
    
   

    

     

    
    

     
 break;
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     

      			}
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      //交换值
     
    
   

    

     

    
    

     
	public static void swap(int[] arr, int index1, int index2) {
     
    
   

    

     

    
    

     
		int tmp = arr[index1];
     
    
   

    

     

    
    

     

      		arr[index1] = arr[index2];
     
    
   

    

     

    
    

     

      		arr[index2] = tmp;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      //打印
     
    
   

    

     

    
    

     
	public static void printArray(int[] arr) {
     
    
   

    

     

    
    

     
		for (int i = 0; i != arr.length; i++) {
     
    
   

    

     

    
    

     

      			System.out.print(arr[i] + " ");
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     

      		System.out.println();
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
	public static void main(String[] args) {
     
    
   

    

     

    
    

     
		int[] arr = { 6, 9, 1, 3, 1, 2, 2, 5, 6, 1, 3, 5, 9, 7, 2, 5, 6, 1, 9 };
     
    
   

    

     

    
    

     
		// sorted : { 1, 1, 1, 1, 2, 2, 2, 3, 3, 5, 5, 5, 6, 6, 6, 7, 9, 9, 9 }
     
    
   

    

     

    
    

     

      		printArray(getMinKNumsByBFPRT(arr, 10));
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      }
     
    
  
 

这个办法解决了最差的退化情况，在一大堆数中求其前k大或前k小的问题，简称TOP-K问题。目前解决TOP-K问题最有效的算法即是BFPRT算法，其又称为中位数的中位数算法，该算法由Blum、Floyd、Pratt、Rivest、Tarjan提出 ，让我们永远记住这群伟大的人。

文章来源: fantianzuo.blog.csdn.net，作者：兔老大RabbitMQ，版权归原作者所有，如需转载，请联系作者。

原文链接：fantianzuo.blog.csdn.net/article/details/103571762