排序算法基本介绍及python实现(含详细注释)
对数组排序可以说是编程基础中的基础,本文对八种排序方法做简要介绍并用python实现。
代码中注释很全,适合复习和萌新学习。这是刚入学自己写的,可能难免比不上标准的写法,但是懒得改了。
文末会放和排序相关的基本拓展总结链接。
看不明白可以看群里视频
注意排序实现的具体方式,不要用局部变量,否则占空间太多,和空间复杂度不符。
好,我们开始。
- 选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在待排序序列的起始位置,直到全部待排序的数据元素排完。时间复杂度O(N^2)
-
for i in range(len(l)):#意义是第i个位置开始挑第i大(小)的元素
-
for j in range(i,len(l)):#和其他待排序的元素比较
-
if l[j]<l[i]:#更大就交换
-
l[j],l[i]=l[i],l[j]
- 冒泡排序
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的元素列,一次比较两个相邻的元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换(一般进行n次即可,第n次一定会把第n小的元素放到正确位置)。
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。时间复杂度O(N^2)
-
for i in range(len(l)-1):#下标和i无关,代表的只是第i次排序,最多需要len(l)-1次排序即可
-
for j in range(len(l)-1):#遍历每一个元素
-
if l[j]<l[j+1]:#本元素比下一个元素小,就交换
-
l[j],l[j+1]=l[j+1],l[j]
分析一下其实每次排序都会多一个元素已经确定了位置,不需要再次遍历。
所以j循环可以改成len(l)-i-1
时间复杂度没变。
- 插入排序
有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,但要求插入后此数据序列仍然有序,这个时候就要用到一种新的排序方法——插入排序法,插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序,时间复杂度为O(n^2)。是稳定的排序方法。
-
for i in range(1,len(l)):#意义是第i个元素开始插入i之前的序列(已经有序)
-
for j in range(i,0,-1):#只要比它之前的元素小就交换
-
if l[j]<l[j-1]:
-
l[j],l[j-1]=l[j-1],l[j]
-
else:
-
break#直到比前一个元素大
- 归并排序
速度仅次于快速排序,为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列
试想:假设已经有两个有序数列,分别存放在两个数组s,r中,我们如何把他们有序的合并在一起?
归并排序就是在重复这样的过程,首先单个元素合并为含有两个元素的数组(有序),然后这种数组再和同类数组合并为四元素数组,以此类推,直到整个数组合并完毕。
-
def gg(l,ll):#合并函数
-
a,b=0,0
-
k=[]#用来合并的列表
-
while a<len(l) and b<len(ll):#两边都非空
-
if l[a]<ll[b]:
-
k.append(l[a])
-
a=a+1
-
elif l[a]==ll[b]:a=a+1#实现去重
-
else:
-
k.append(ll[b])
-
b=b+1
-
k=k+l[a:]+ll[b:]#加上剩下的
-
return k
-
-
def kk(p):#分到只剩一个元素就开始合并
-
if len(p)<=1:
-
return p
-
a=kk(p[0:len(p)//2])#不止一个元素就切片
-
b=kk(p[len(p)//2:])
-
return gg(a,b)#返回排好序的一部分
-
l=list(map(int,input().split(" ")))
-
print(kk(l))
- 快速排序
快速排序(Quicksort)是对冒泡排序的一种改进。
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
- 随机化快排
快速排序的最坏情况基于每次划分对主元的选择。基本的快速排序选取第一个元素作为主元。这样在数组已经有序的情况下,每次划分将得到最坏的结果。比如1 2 3 4 5,每次取第一个元素,就退化为了O(N^2)。一种比较常见的优化方法是随机化算法,即随机选取一个元素作为主元。
这种情况下虽然最坏情况仍然是O(n^2),但最坏情况不再依赖于输入数据,而是由于随机函数取值不佳。实际上,随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度。
进一步提升可以分割为三部分,即小于区,等于区,大于区,减小了递归规模,并克服了多元素相同的退化。
-
def gg(a,b):
-
global l
-
if a>=b:#注意停止条件,我以前没加>卡了半小时
-
return
-
x,y=a,b
-
import random#为了避免遇到基本有序序列退化,随机选点
-
g=random.randint(a,b)
-
l[g],l[y]=l[y],l[g]#交换选中元素和末尾元素
-
while a<b:
-
if l[a]>l[y]:#比目标元素大
-
l[a],l[b-1]=l[b-1],l[a]#交换
-
b=b-1#大于区扩大
-
#注意:换过以后a不要加,因为新换过来的元素并没有判断过
-
else:a=a+1#小于区扩大
-
l[y],l[a]=l[a],l[y]#这时a=b
-
#现在解释a和b:a的意义是小于区下一个元素
-
#b是大于区的第一个元素
-
gg(x,a-1)#左右分别递归
-
gg(a+1,y)
-
-
l=list(map(int,input().split(" ")))
-
gg(0,len(l)-1)
-
print(l)
- 堆排序
堆排序(HeapSort)是一树形选择排序。堆排序的特点是:在排序过程中,将R[l..n]看成是一棵完全二叉树的顺序存储结构,利用完全二叉树中双亲结点和孩子结点之间的内在关系,在当前无序区中选择关键字最大(或最小)的记录。
由于建初始堆所需的比较次数较多,所以堆排序不适宜于记录数较少的文件。
堆排序是就地排序,辅助空间为O(1).
它是不稳定的排序方法。
主要思想:维持一个大根堆(根结点(亦称为堆顶)的关键字是堆里所有结点关键字中最大者,称为大根堆,又称最大堆。注意:①堆中任一子树亦是堆。②以上讨论的堆实际上是二叉堆(Binary Heap),类似地可定义k叉堆。)
第一步:通过调整原地建立大根堆
第二步:每次交换堆顶和边界元素,并减枝,然后调整堆顶下沉到正确位置。
-
def down(i,k):#在表l里的第i元素调整,k为边界
-
-
#优先队列也是通过这种方式实现的
-
global l
-
while 2*i+2<k:#右孩子不越界
-
lift,right=2*i+1,2*i+2
-
m=max(l[i],l[lift],l[right])
-
if m==l[i]:#不需要调
-
break
-
if m==l[lift]:#把最大的换上来
-
l[i],l[lift]=l[lift],l[i]
-
i=lift#目的节点下标更新
-
else:#把最大的换上来
-
l[i],l[right]=l[right],l[i]
-
i=right#目的节点下标更新
-
if 2*i+1<k:#判断左孩子
-
if l[2*i+1]>l[i]:
-
l[i],l[2*i+1]=l[2*i+1],l[i]
-
-
def main():
-
global l
-
for j in range(1,len(l)+1):#调大根堆
-
i=len(l)-j
-
down(i,len(l))
-
for i in range(len(l)-1,-1,-1):#排序
-
l[i],l[0]=l[0],l[i]#最大和边界交换,剪枝
-
down(0,i)
-
print(l)
-
-
l=list(map(int,input().split(" ")))
-
main()
-
-
-
-
-
- 桶排序
桶排序不是基于比较的排序方法,只需对号入座。将相应的数字放进相应编号的桶即可。
当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间o(n)
对于海量有范围数据十分适合,比如全国高考成绩排序,公司年龄排序等等。
-
l=list(map(int,input().split(" ")))
-
n=max(l)-min(l)
-
p=[0]*(n+1)#为了省空间
-
for i in l:
-
p[i-min(l)]=1#去重排序,做标记即可
-
for i in range(n):
-
if p[i]==1:#判断是否出现过
-
print(i+min(l),end=" ")
- 希尔排序
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
通过缩小有序步长来实现。
-
def shell(arr):
-
n=len(arr)#初始化步长
-
h=1
-
while h<n/3:
-
h=3*h+1
-
while h>=1:#判断,退出后就有序了。
-
for i in range(h,n):
-
j=i
-
while j>=h and arr[j]<arr[j-h]:#判断是否交换
-
arr[j], arr[j-h] = arr[j-h], arr[j]
-
j-=h
-
h=h//3#逐渐缩小步长
-
print arr
稳定性及时间复杂度
排序稳定性概念:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
时间复杂度:时间复杂度是同一问题可用不同算法解决,而一个算法的质量优劣将影响到算法乃至程序的效率。算法分析的目的在于选择合适算法和改进算法。可以理解为和常数操作所成的一种关系(常数操作为O(1))
空间复杂度类似。
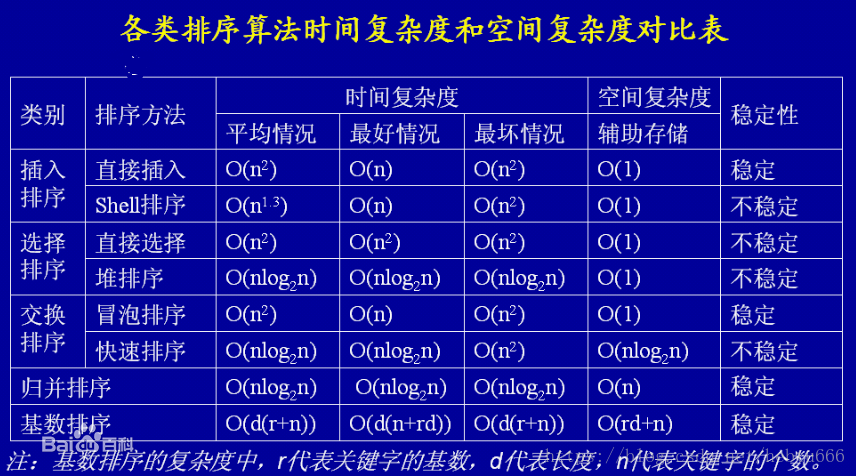
下面给出各类排序的对比图:
- 基数排序
因为桶排序是稳定的,基数排序就是很多次桶排序而已,按位进行桶排序即可。
(个人认为桶排序名字不恰当,因为桶是先进后出,和稳定的算法正好反了,)
总:
比较排序和非比较排序
常见的排序算法都是比较排序,非比较排序包括计数排序、桶排序和基数排序,非比较排序对数据有要求,因为数据本身包含了定位特征,所有才能不通过比较来确定元素的位置。
比较排序的时间复杂度通常为O(n2)或者O(nlogn),比较排序的时间复杂度下界就是O(nlogn),而非比较排序的时间复杂度可以达到O(n),但是都需要额外的空间开销。
- 若n较小(数据规模较小),插入排序或选择排序较好
- 若数据初始状态基本有序(正序),插入、冒泡或随机快速排序为宜
- 若n较大,则采用时间复杂度为O(nlogn)的排序方法:快速排序或堆排序
- 快速排序是目前基于比较的排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
- 堆排序所需的辅助空间少于快速排序,并且不会出现快速排序可能出现的最坏情况。这两种排序都是不稳定的。
各种拓展以后放链接
归并求逆序:https://blog.csdn.net/hebtu666/article/details/81773190
快排前k小:https://blog.csdn.net/hebtu666/article/details/81772978这个bfprt算法以后再写,也不难。
快排荷兰国旗:https://blog.csdn.net/hebtu666/article/details/81772701
堆:https://blog.csdn.net/hebtu666/article/details/81706288
文章来源: fantianzuo.blog.csdn.net,作者:兔老大RabbitMQ,版权归原作者所有,如需转载,请联系作者。
原文链接:fantianzuo.blog.csdn.net/article/details/81434236
- 点赞
- 收藏
- 关注作者


评论(0)