二叉搜索树实现
本文给出二叉搜索树介绍和实现
首先说它的性质:所有的节点都满足,左子树上所有的节点都比自己小,右边的都比自己大。
那这个结构有什么有用呢?
首先可以快速二分查找。还可以中序遍历得到升序序列,等等。。。
基本操作:
1、插入某个数值
2、查询是否包含某个数值
3、删除某个数值
根据实现不同,还可以实现其他很多种操作。
实现思路思路:
前两个操作很好想,就是不断比较,大了往左走,小了往右走。到空了插入,或者到空都没找到。
而删除稍微复杂一些,有下面这几种情况:
1、需要删除的节点没有左儿子,那就把右儿子提上去就好了。
2、需要删除的节点有左儿子,这个左儿子没有右儿子,那么就把左儿子提上去
3、以上都不满足,就把左儿子子孙中最大节点提上来。
当然,反过来也是成立的,比如右儿子子孙中最小的节点。
下面来叙述为什么可以这么做。
下图中A为待删除节点。
第一种情况:
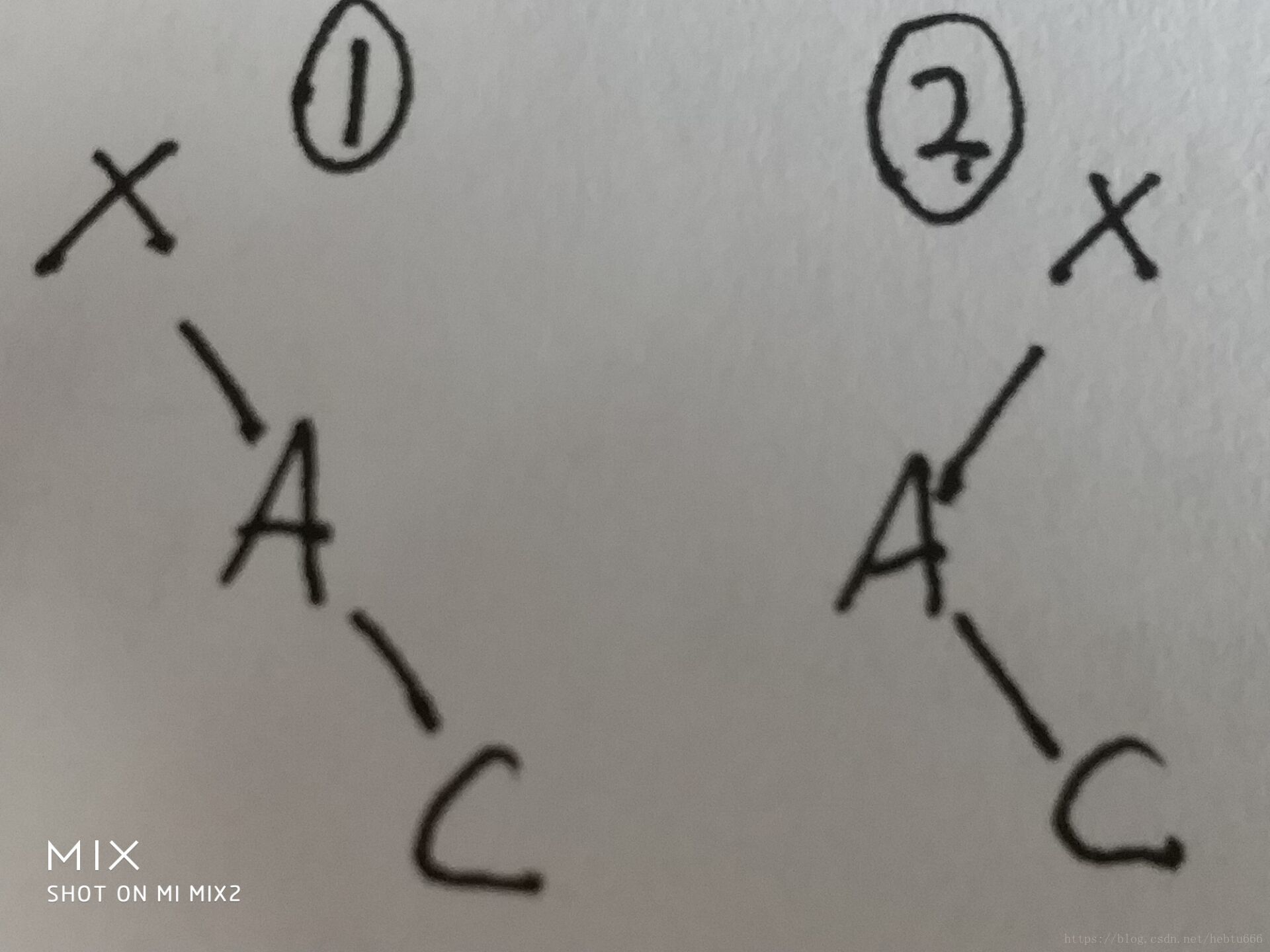
1、去掉A,把c提上来,c也是小于x的没问题。
2、根据定义可知,x左边的所有点都小于它,把c提上来不影响规则。
第二种情况
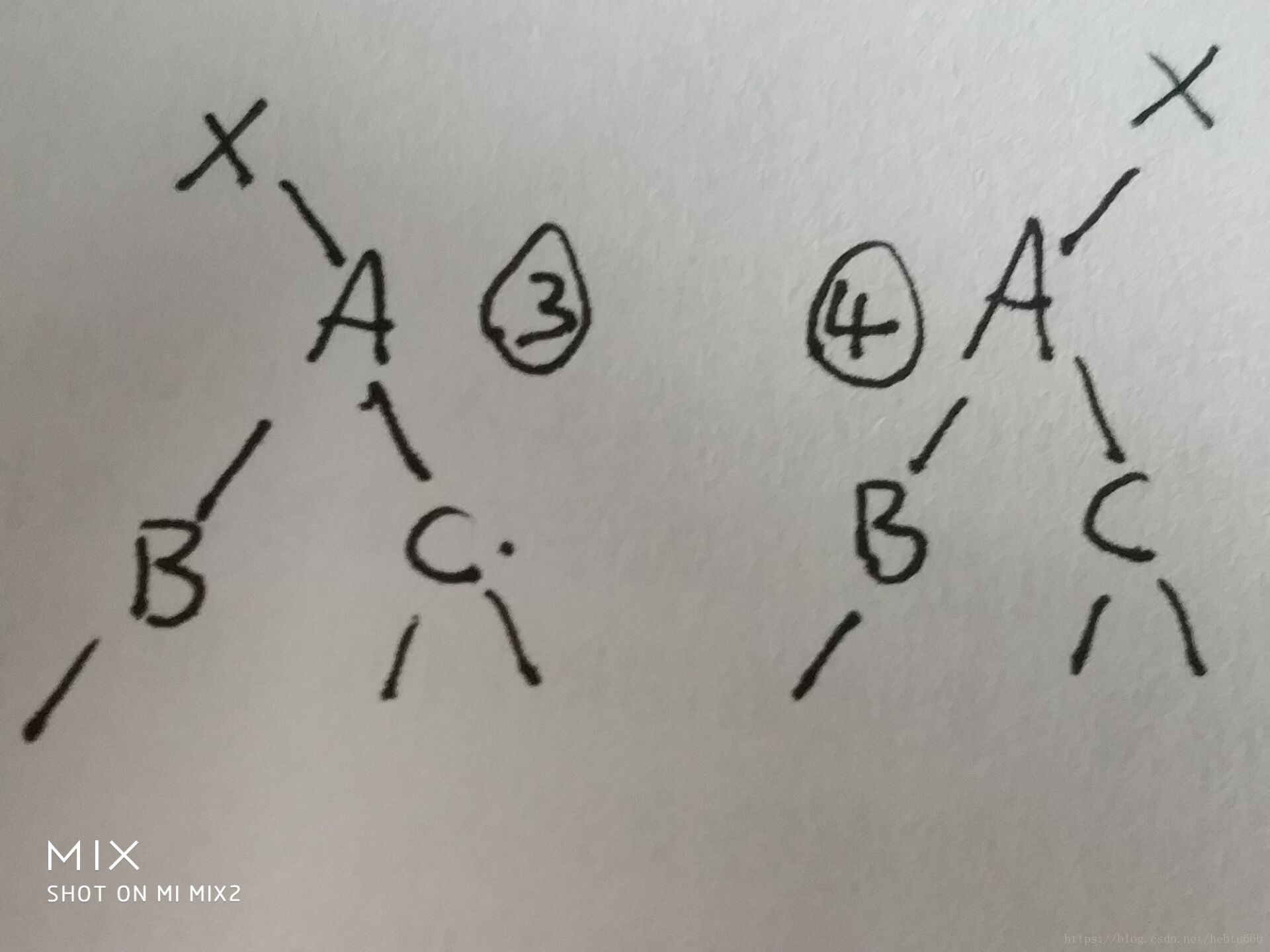
3、B<A<C,所以B<C,根据刚才的叙述,B可以提上去,c可以放在b右边,不影响规则
4、同理
第三种情况
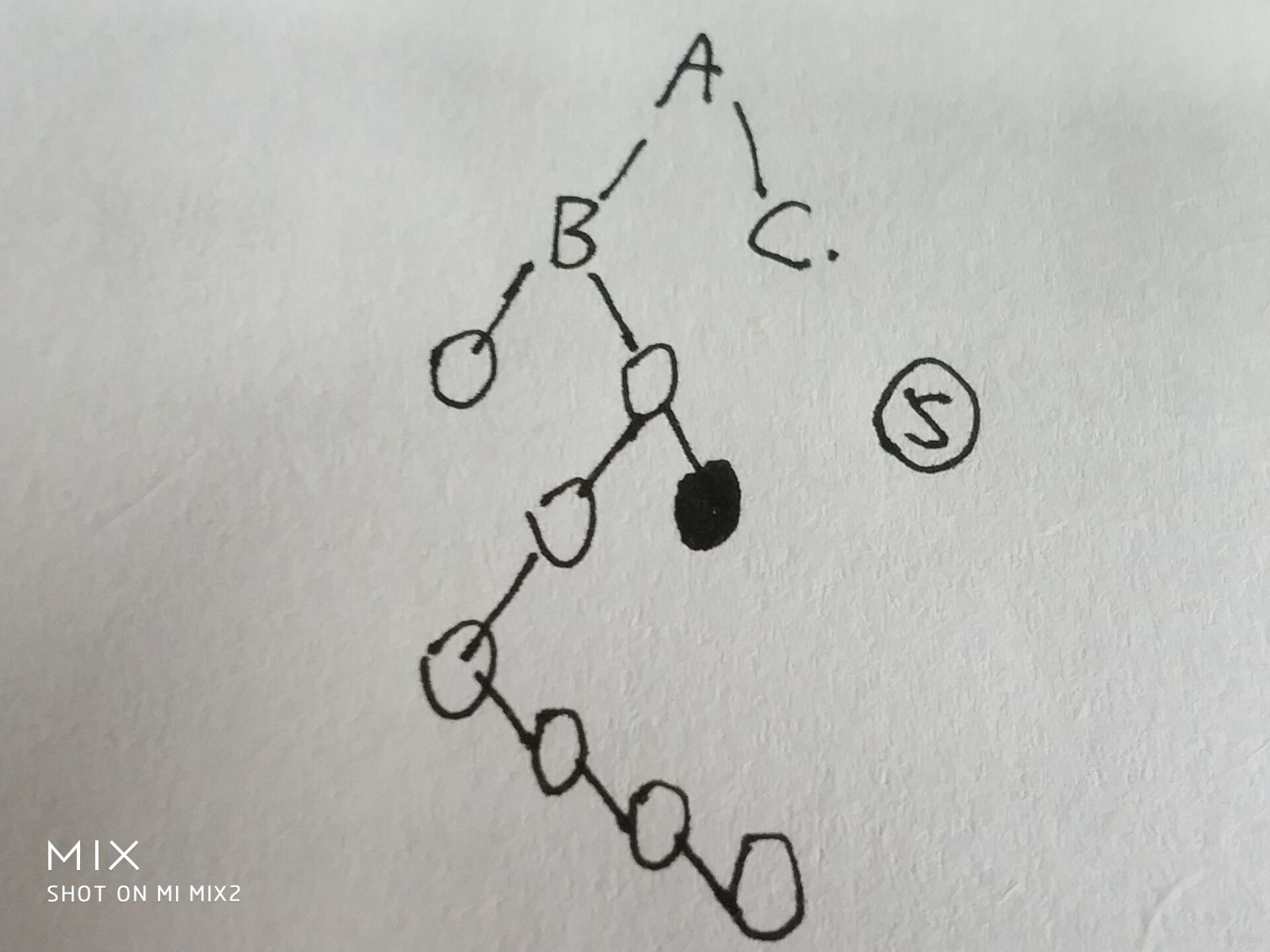
5、注意:是把黑色的提升上来,不是所谓的最右边的那个,因为当初向左拐了,他一定小。
因为黑色是最大,比B以及B所有的孩子都大,所以让B当左孩子没问题
而黑点小于A,也就小于c,所以可以让c当右孩子
大概证明就这样。。
下面我们用代码实现并通过注释理解
上次链表之类的用的c,循环来写的。这次就c++函数递归吧,不同方式练习。
定义
-
struct node
-
{
-
int val;//数据
-
node *lch,*rch;//左右孩子
-
};
插入
-
node *insert(node *p,int x)
-
{
-
if(p==NULL)//直到空就创建节点
-
{
-
node *q=new node;
-
q->val=x;
-
q->lch=q->rch=NULL;
-
return p;
-
}
-
if(x<p->val)p->lch=insert(p->lch,x);
-
else p->lch=insert(p->rch,x);
-
return p;//依次返回自己,让上一个函数执行。
-
}
查找
-
bool find(node *p,int x)
-
{
-
if(p==NULL)return false;
-
else if(x==p->val)return true;
-
else if(x<p->val)return find(p->lch,x);
-
else return find(p->rch,x);
-
}
删除
-
node *remove(node *p,int x)
-
{
-
if(p==NULL)return NULL;
-
else if(x<p->val)p->lch=remove(p->lch,x);
-
else if(x>p->val)p->lch=remove(p->rch,x);
-
//以下为找到了之后
-
else if(p->lch==NULL)//情况1
-
{
-
node *q=p->rch;
-
delete p;
-
return q;
-
}
-
else if(p->lch->rch)//情况2
-
{
-
node *q=p->lch;
-
q->rch=p->rch;
-
delete p;
-
return q;
-
}
-
else
-
{
-
node *q;
-
for(q=p->lch;q->rch->rch!=NULL;q=q->rch);//找到最大节点的前一个
-
node *r=q->rch;//最大节点
-
q->rch=r->lch;//最大节点左孩子提到最大节点位置
-
r->lch=p->lch;//调整黑点左孩子为B
-
r->rch=p->rch;//调整黑点右孩子为c
-
delete p;//删除
-
return r;//返回给父
-
}
-
return p;
-
}
文章来源: fantianzuo.blog.csdn.net,作者:兔老大RabbitMQ,版权归原作者所有,如需转载,请联系作者。
原文链接:fantianzuo.blog.csdn.net/article/details/81741034
- 点赞
- 收藏
- 关注作者


评论(0)