假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶
示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

记忆化搜索

  

   

    

     

    
    

     

      public class Solution {
     
    
   

    

     

    
    

     
 public int climbStairs(int n) {
     
    
   

    

     

    
    

     
 int memo[] = new int[n + 1];
     
    
   

    

     

    
    

     
 return climb_Stairs(0, n, memo);
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     
 public int climb_Stairs(int i, int n, int memo[]) {
     
    
   

    

     

    
    

     
 if (i > n) {
     
    
   

    

     

    
    

     
 return 0;
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     
 if (i == n) {
     
    
   

    

     

    
    

     
 return 1;
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     
 if (memo[i] > 0) {
     
    
   

    

     

    
    

     
 return memo[i];
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     

       memo[i] = climb_Stairs(i + 1, n, memo) + climb_Stairs(i + 2, n, memo);
     
    
   

    

     

    
    

     
 return memo[i];
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     

      }
     
    
  
 

dp

  

   

    

     

    
    

     

      public class Solution {
     
    
   

    

     

    
    

     
 public int climbStairs(int n) {
     
    
   

    

     

    
    

     
 if (n == 1) {
     
    
   

    

     

    
    

     
 return 1;
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     
 int[] dp = new int[n + 1];
     
    
   

    

     

    
    

     

       dp[1] = 1;
     
    
   

    

     

    
    

     

       dp[2] = 2;
     
    
   

    

     

    
    

     
 for (int i = 3; i <= n; i++) {
     
    
   

    

     

    
    

     

       dp[i] = dp[i - 1] + dp[i - 2];
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     
 return dp[n];
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     

      }
     
    
  
 

优化空间

  

   

    

     

    
    

     

      public class Solution {
     
    
   

    

     

    
    

     
 public int climbStairs(int n) {
     
    
   

    

     

    
    

     
 if (n == 1) {
     
    
   

    

     

    
    

     
 return 1;
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     
 int first = 1;
     
    
   

    

     

    
    

     
 int second = 2;
     
    
   

    

     

    
    

     
 for (int i = 3; i <= n; i++) {
     
    
   

    

     

    
    

     
 int third = first + second;
     
    
   

    

     

    
    

     

       first = second;
     
    
   

    

     

    
    

     

       second = third;
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     
 return second;
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     

      }
     
    
  
 

矩阵快速幂

  

   

    

     

    
    

     

      public class Solution {
     
    
   

    

     

    
    

     
   public int climbStairs(int n) {
     
    
   

    

     

    
    

     
 int[][] q = {{1, 1}, {1, 0}};
     
    
   

    

     

    
    

     
 int[][] res = pow(q, n);
     
    
   

    

     

    
    

     
 return res[0][0];
     
    
   

    

     

    
    

     

         }
     
    
   

    

     

    
    

     
   public int[][] pow(int[][] a, int n) {
     
    
   

    

     

    
    

     
 int[][] ret = {{1, 0}, {0, 1}};
     
    
   

    

     

    
    

     
 while (n > 0) {
     
    
   

    

     

    
    

     
 if ((n & 1) == 1) {
     
    
   

    

     

    
    

     

       ret = multiply(ret, a);
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     

       n >>= 1;
     
    
   

    

     

    
    

     

       a = multiply(a, a);
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     
 return ret;
     
    
   

    

     

    
    

     

         }
     
    
   

    

     

    
    

     
   public int[][] multiply(int[][] a, int[][] b) {
     
    
   

    

     

    
    

     
 int[][] c = new int[2][2];
     
    
   

    

     

    
    

     
 for (int i = 0; i < 2; i++) {
     
    
   

    

     

    
    

     
 for (int j = 0; j < 2; j++) {
     
    
   

    

     

    
    

     

       c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     
 return c;
     
    
   

    

     

    
    

     

         }
     
    
   

    

     

    
    

     

      }
     
    
  
 

公式

  

   

    

     

    
    

     

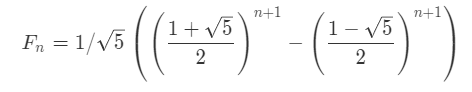
      public class Solution {
     
    
   

    

     

    
    

     
 public int climbStairs(int n) {
     
    
   

    

     

    
    

     
 double sqrt5=Math.sqrt(5);
     
    
   

    

     

    
    

     
 double fibn=Math.pow((1+sqrt5)/2,n+1)-Math.pow((1-sqrt5)/2,n+1);
     
    
   

    

     

    
    

     
 return (int)(fibn/sqrt5);
     
    
   

    

     

    
    

     

       }
     
    
   

    

     

    
    

     

      }
     
    
  
 

文章来源: fantianzuo.blog.csdn.net，作者：兔老大RabbitMQ，版权归原作者所有，如需转载，请联系作者。

原文链接：fantianzuo.blog.csdn.net/article/details/103201337