一.二叉树

1.二叉树的定义

把满足以下条件的树结构称为二叉树：

1.每个结点的度都不大于2.

2.每个结点的孩子结点次序不能任意颠倒。

2.二叉树的性质

性质1：在二叉树的第k层上,最多有2^(k-1)（k≥1）个结点。

性质2：深度为m的二叉树最多有2m-1（m≥1）个结点。

性质3：在任意一棵二叉树中,如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1。

性质4：具有n个结点的二叉树,其深度至少为〔log2n〕+1,其中〔log2n〕表示取log2n的整数部分。

性质5：如果对一棵有n个结点的完全二叉树按照从上到下和从左到右的顺序对所有结点进行从1开始顺序编号，则对于任意的序号为i的结点有：

①如 i =1，则结点i是二叉树的根，无双亲，如 i > 1，则序号为i的结点的双亲结点序号为i/2。

②如 2i > n，则序号为i的结点无左孩子，如 2i ≤ n，则序号为i的结点的左孩子结点的序号为2i。

③如 2i+1 > n，则序号为i的结点无右孩子，如 2i+1 ≤ n，则序号为i的结点的右孩子结点的序号为2i+1。

3.二叉树的存储结构

二叉树的结构是非线性的，每一个结点最多可有两个后继。二叉树的存储结构分为顺序存储结构和链式存储结构。

1).顺序存储结构

顺序存储结构可以用一维数组来实现，如下图：

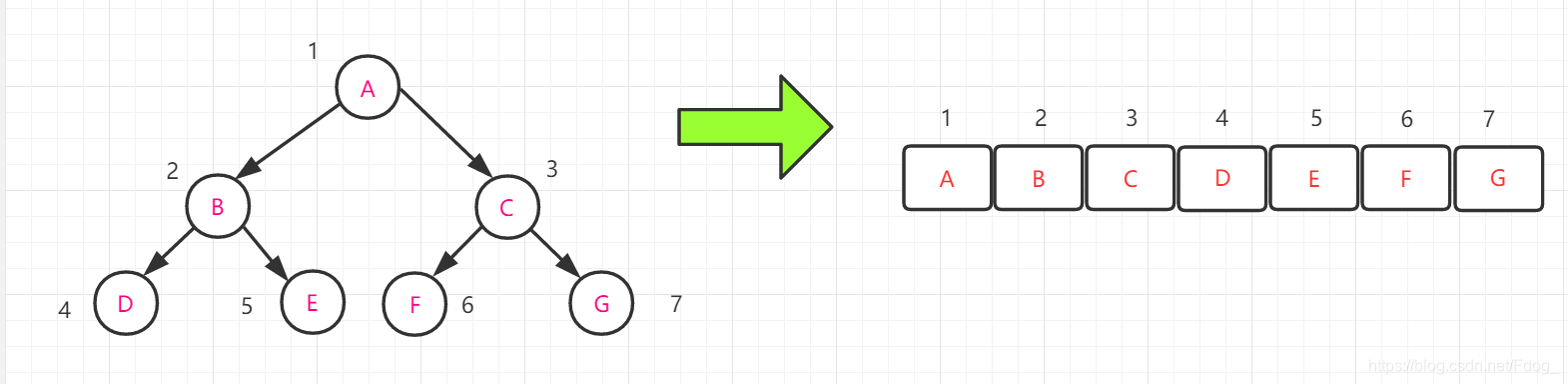
可以看出，当二叉树为完全二叉树时，这种存储结构很方便，而且不浪费空间，但是对于一般的二叉树，必须用“虚结点”将其补成一个完整的完全二叉树来存储，这就造成了空间浪费，如下图：

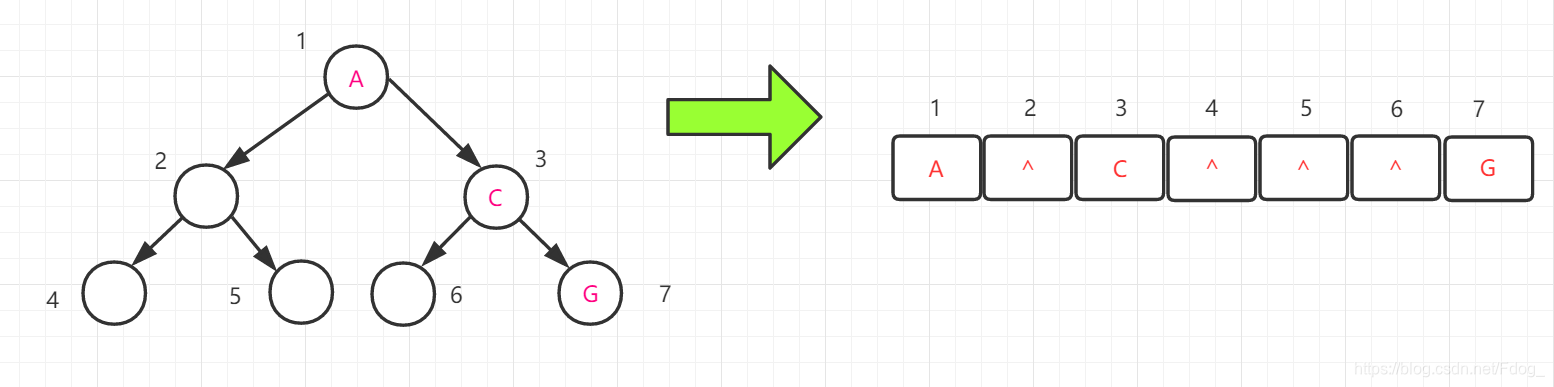
因此，顺序存储一般适用于完全二叉树，既然顺序存储不能满足对二叉树的存储需求，那么可以使用链式存储，如下图。

2).链式存储结构

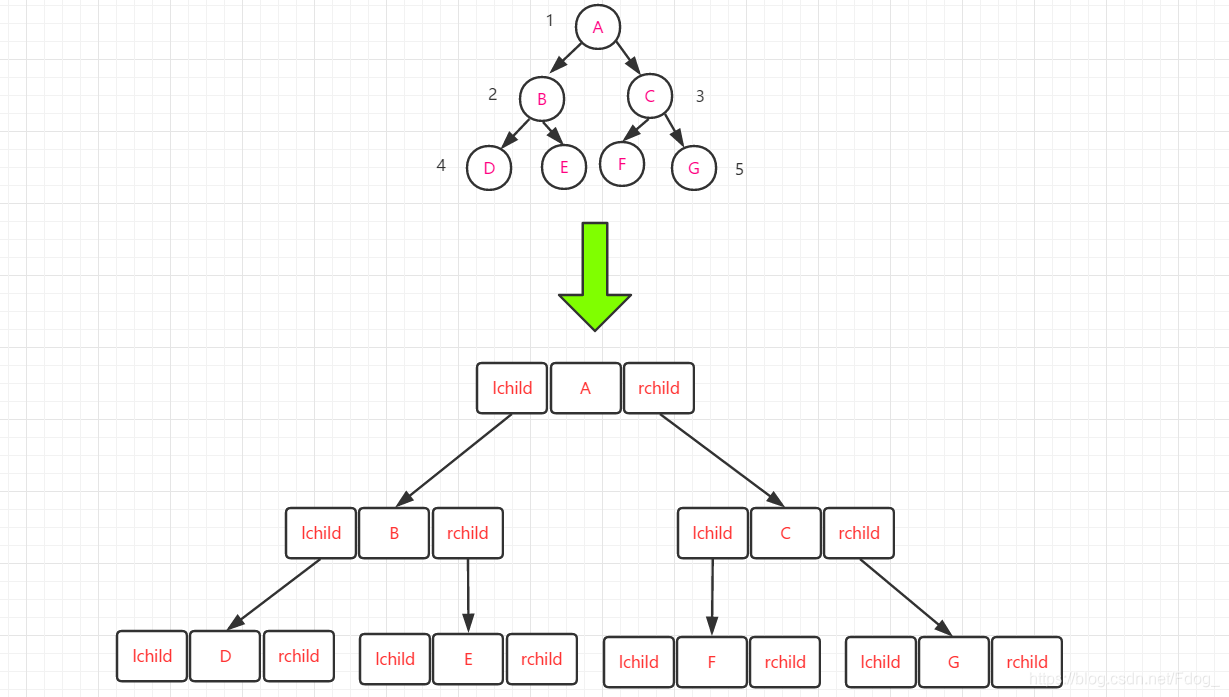
对于任意二叉树，每个结点只有一个双亲结点（根除外），最多有两个孩子，便可以设计成上图所示结构：【lchind data rchild】。该二叉树实现方式又称为二叉链表。

3).结点代码实现

二叉链表结点结构代码实现如下：

typedef struct Node
{ DataType data; struct Node * LChild; struct Node * RChild;
}BiTNode,*BiTree;
  

 

  
1
  
2
  
3
  
4
  
5
 

二.二叉树的遍历(重点)

1.遍历理论过程

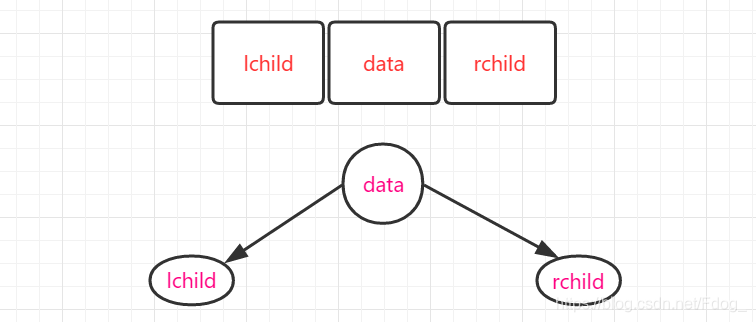
如果用LDR表示遍历左子树，根结点，右子树，则有如下6种遍历顺序：

①访问根，遍历右子树，遍历左子树。记作DRL

②访问根，遍历左子树，遍历右子树。记作DLR

③遍历左子树，访问根结点，遍历右子树。记作LDR

④遍历右子树，访问根结点，遍历左子树。记作RDL

⑤遍历左子树，遍历右子树，访问根结点。记作LRD

⑥遍历右子树，遍历左子树，访问根结点。记作RLD

如果规定按先左后右的顺序遍历，则只剩下三种：DLR , LDR , LRD。

然后根据对根访问顺序的不同，分别称DLR为前序遍历，LDR为中序遍历，LRD为后序遍历。

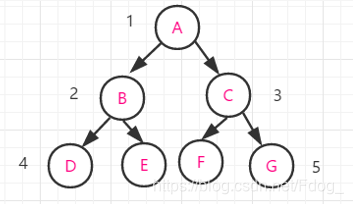
对于上述的二叉树：
前序遍历顺序：A B D E C F G
中序遍历顺序：D B E A F C G
后序遍历顺序：D E B F G C A

写成这样,我觉得会更有助于萌新的理解：

前序遍历顺序：(A)    (B (DE) )    (C (FG) )
中序遍历顺序：((D) B (E))    (A)    ((F) C (G))
后序遍历顺序：( (DE) B)    ( (FG) C)    (A)

先将大头写下来然后进行填写，类似于填空，但是仅限于帮助你理解遍历顺序，而不是让你使用这个方法记忆遍历顺序，我们应该通过辅助工具来帮助我们真正了解。

下面再出一个练练手：

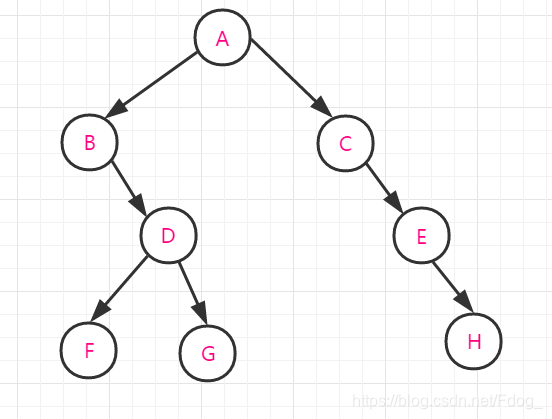
试着写一写是不是和下面的答案一样呢，如果一样，说明你学会了！
前序遍历：A B D F G C E H
中序遍历：B F D G A C E H
后序遍历：F G D B H E C A

下面用代码来实现各种遍历。

2.前序遍历

void PreOrder(BiTree root)
{ // root为指向二叉树或某一树的根结点 if(root!=NULL) { Visit(root->data); // 访问根结点，显示数据结点 PreOrder(root->LChild);// 遍历左子树 PreOrder(root->RChild);// 遍历右子树 }
}
  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

3.中序遍历

void PreOrder(BiTree root)
{ if(root!=NULL) { PreOrder(root->LChild); Visit(root->data) PreOrder(root->RChild); }
}
  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

4.后序遍历

void PreOrder(BiTree root)
{ if(root!=NULL) { PreOrder(root->LChild); PreOrder(root->RChild); Visit(root->data); }
}
  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
 

虽然理论知识对于二叉树的遍历很复杂，但是由于二叉树是一种递归定义的结构，先序，中序，后序，便是递归定义的。故采用递归的方式遍历二叉树的代码量很少。

若有错误，欢迎指正批评，欢迎评论。
每文一句：没有人会为你的贫穷负责，却有人为你的富有而喝彩！所以不要活在别人的嘴巴里，做好自己！有路，就大胆地去走；有梦，就大胆地飞翔；前行的路，不怕万人阻挡，只怕自己投降！

文章来源: blog.csdn.net，作者：花狗Fdog，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/Fdog_/article/details/104782153