C++ 解决大数运算(大数加法,大数幂运算,大数求余)
【摘要】
文章目录
1. 大数加法2. 大数幂运算3.大数求余
废话不多说,直接上代码了。
1. 大数加法
string getCountAdd(string a, string b)
{
string c = "";
int bit = -1; //判断是否进位 -1为否,其他为进位数
int i = a.length()-1; //获得a字符串...
废话不多说,直接上代码了。
1. 大数加法
string getCountAdd(string a, string b)
{
string c = "";
int bit = -1; //判断是否进位 -1为否,其他为进位数
int i = a.length()-1; //获得a字符串长度
int j = b.length()-1; //获得b字符串长度
//第一种情况 两者都处理完
while (i != -1 && j != -1)
{
int t1 = a[i] - 48; int t2 = b[j] - 48;
//不存在进位
if (bit == -1)
{ if (t1 + t2 >= 10) { int d = (t1 + t2) % 10; c.insert(0, 1, d + 48); bit = (t1 + t2) / 10; } else { c.insert(0, 1, t1 + t2 + 48); }
}
//存在进位
else
{ if (t1 + t2 + bit >= 10) { int d = (t1 + t2 + bit) % 10; c.insert(0, 1, d + 48); bit = (t1 + t2 + bit) / 10; } else { c.insert(0, 1, t1 + t2 + bit + 48); bit = -1; }
}
i--;
j--;
}
//第二种情况 前者处理完
while (i == -1 && j != -1)
{
int t2 = b[j] - 48;
if (bit == -1)
{ c.insert(0, 1, b[j]);
}
else
{ if (t2 + bit >= 10) { int d = (t2 + bit) % 10; c.insert(0, 1, d + 48); bit = (t2 + bit) / 10; } else { c.insert(0, 1, t2 + bit + 48); bit = - 1; }
}
j--;
}
//第三种情况 后者处理完
while (i != -1 && j == -1)
{
int t1 = a[i] - 48;
if (bit == -1)
{ c.insert(0, 1, a[i]);
}
else
{ if (t1 + bit >= 10) { int d = (t1 + bit) % 10; c.insert(0, 1, d + 48); bit = (t1 + bit) / 10; } else { c.insert(0, 1, t1 + bit + 48); bit = -1; }
}
i--;
}
//最后再判断是否存在进位
if (bit != -1)
{
c.insert(0, 1, bit + 48);
}
bit = -1;
return c;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99

2. 大数幂运算
string getCountExp(int a, int b)
{
string a1 = to_string(a);
int i = a1.length()-1;//a的最后下角标
//m位数*n位数长度不会超过m+n位
string temp = a1; //temp一直变化
string temp_2 = "0";
int bitcount = 0; //判断当前位数
int bit = -1;//判断是否存在进位
string * arr = new string[a1.length()];//保存每次计算的数
int arr_i = 0;
for (int x = 1; x < b; x++)//几次方就循环几次
{
while (i != -1)//乘数的位数
{ //temp * a1 int t1 = a1[i] - 48; int j = temp.length() - 1;//temp的最后下角标 for (int z = 0; z < bitcount; z++) { arr[arr_i].insert(0, 1, '0'); } while (j != -1)//temp的位数 { int t2 = temp[j] - 48; if (bit == -1)//判断是否有进位 { if (t1*t2 >= 10) { int d = (t1*t2) % 10; arr[arr_i].insert(0, 1, d + 48); int d_2 = (t1*t2) / 10; bit = d_2; } else { int d = t1*t2; arr[arr_i].insert(0, 1, d + 48); } } else { if ((t1*t2)+bit >= 10) { int d = ((t1*t2) + bit) % 10; arr[arr_i].insert(0, 1, d + 48); int d_2 = ((t1*t2) + bit) / 10; bit = d_2; } else { int d = (t1*t2) + bit; arr[arr_i].insert(0, 1, d + 48); bit = -1; } } j--; } if (bit != -1) { arr[arr_i].insert(0, 1, bit + 48); bit = -1; } //走完一圈 //计算每一位的数,最后相加 //temp_2=temp_2+arr[arr_i]; temp_2 = getCountAdd(temp_2, arr[arr_i]); bitcount++; arr_i++; i--;
}
bitcount = 0;
temp = temp_2;
temp_2 = "0";
//temp_2 = "0";
for (int z = 0; z < arr_i; z++)
{ arr[z] = "";
}
arr_i = 0;
i = a1.length() - 1;//a的最后下角标
}
return temp;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
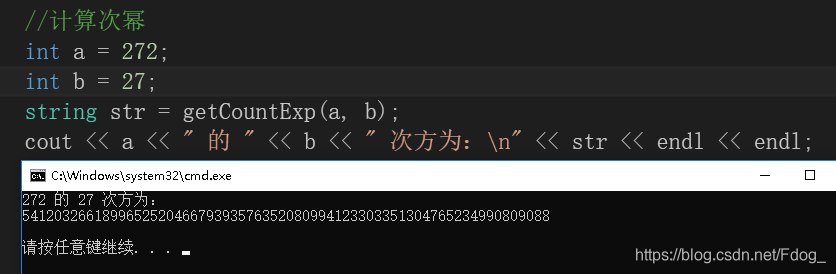
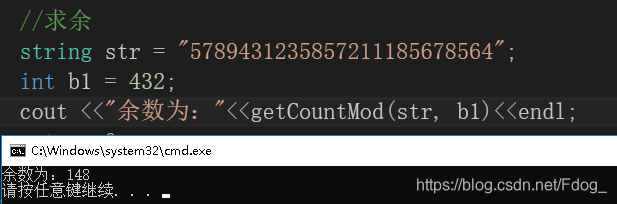
3.大数求余
int getCountMod(string a, int b)
{
int bit = -1; //判断是否需要进位
//例如4255%5
int i = 0;
while (i < a.length())
{
int t1 = a[i] - 48;
if (bit == -1)
{ if (t1%b > 0) { bit = t1%b; }
}
else
{ if (((bit * 10) + t1) % b>=0) { bit = ((bit * 10) + t1) % b; }
}
i++;
}
if (bit != -1)
{
return bit;
}
else
{
return 0;
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
文章来源: blog.csdn.net,作者:花狗Fdog,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/Fdog_/article/details/115432410
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)