查找——线性表
【摘要】
查找的基本概念查找算法的评价指标线性表的查找顺序查找顺序查找的性能分析顺序查找算法特点 折半查找算法描述折半查找性能分析 分块查找(块间有序,块内无序)分块查找性能分析分块查找优缺点
查找的基本概念
查找表:由同一类型的数据元素(或记录)构成的集合静态查找表:查找的同时对查找表不做修改操作(如插入和删除)动态查找表:查找的同时对查找表...
查找的基本概念
- 查找表:由同一类型的数据元素(或记录)构成的集合
- 静态查找表:查找的同时对查找表不做修改操作(如插入和删除)
- 动态查找表:查找的同时对查找表具有修改操作
- 关键字:记录中某个数据项的值,可用来识别一个记录
- 主关键字:唯一标识数据元素
- 次关键字:可以标识若干个数据元素
查找算法的评价指标
- 关键字的平均比较次数,也称平均搜索长度ASL(Average Search Length)

n:记录的个数
pi:查找第i个记录的概率 ( 通常认为pi =1/n )
ci:找到第i个记录所需的比较次数
线性表的查找
顺序查找
- 应用范围:顺序表或线性链表表示的静态查找表表内元素之间无序
- 结构定义
typedef int KeyType; typedef int InfoOther; typedef struct{ KeyType key; // 主键 InfoOther other; // 次键 }ElemType; typedef struct{ ElemType* elem; // 基地址 int length; // 表长 }SSTable;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 顺序查找值为key的元素
int Search_Seq(SSTable ST,KeyType key){ for (int i=1; i<= ST.length; i++) if (ST.elem[i].key == key) return i; return 0; }- 1
- 2
- 3
- 4
- 5
- 改进,加入“哨兵”
int Search_Seq(SSTable ST,KeyType key){ //若成功返回其位置信息,否则返回0 ST.elem[0].key = key; for (int i=ST.length; ST.elem[i].key != key; i--); return i; }- 1
- 2
- 3
- 4
- 5
- 6
顺序查找的性能分析
- 空间复杂度:一个辅助空间
- 时间复杂度:
- 查找成功时的平均查找长度
设表中各记录查找概率相等
ASLs(n)=(1+2+ … +n)/n =(n+1)/2 - 查找不成功时的平均查找长度 ASLf =n+1
- 查找成功时的平均查找长度
顺序查找算法特点
-
算法简单,对表结构无任何要求(顺序和链式)
-
n很大时查找效率较低
-
改进措施:非等概率查找时,可按照查找概率进行排序。
查找概率相等时,ASL相同;
查找概率不等时,如果从前向后查找,则按查找概率由大到小排列的有序表其ASL要比无序表ASL小
折半查找
若k==R[mid].key,查找成功
若k<R[mid].key,则high=mid-1
若k>R[mid].key,则low=mid+1
直至low>high时,查找失败
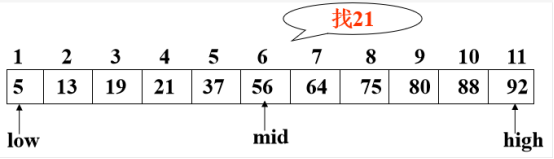
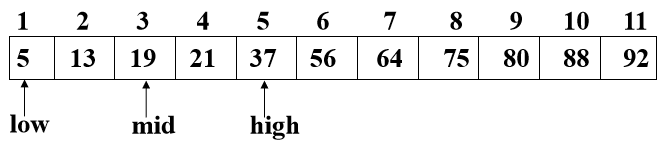
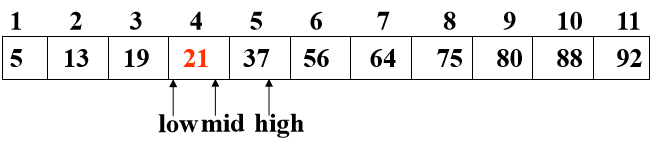
- 设表长为n,low、high和mid分别指向待查元素所在区间的上界、下界和中点,k为给定值
- 初始时,令low=1,high=n,mid=(low+high)/2
- 让k与mid指向的记录比较
- 若k==R[mid].key,查找成功
- 若k<R[mid].key,则high=mid-1
- 若k>R[mid].key,则low=mid+1
- 重复上述操作,直至low>high时,查找失败
算法描述
/*-----------折半查找----------*/
// 非递归算法
// 适用于顺序存储
int Search_Bin(SSTable ST, KeyType key){
//若找到,则函数值为该元素在表中的位置,否则为0
int low = 1;
int high = ST.length;
while(low <= high){
int mid = (low + high) / 2;
if(key == ST.elem[mid].key) return mid;
else if(key < ST.elem[mid].key) high = mid - 1; //前一子表查找
else low = mid + 1; //后一子表查找
}
return 0; //表中不存在待查元素
}
/*-----------折半查找----------*/
// 递归算法
int Search_Bin(SSTable ST, KeyType key, int low, int high){
if(low > high) return 0;
int mid = (low + high) / 2;
if(key == ST.elem[mid].key) return mid;
else if(key < ST.elem[mid].key) Search_Bin(ST, key, low, mid-1);
else Search_Bin(ST, key, mid+1, high);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
折半查找性能分析
-
查找成功时比较次数:为该结点在判定树上的层次数,不超过树的深度 d = log2 n + 1 (log向下取整)
-
查找不成功的过程就是走了一条从根结点到外部结点的路径d或d-1。
-
查找过程:每次将待查记录所在区间缩小一半,比顺序查找效率高,时间复杂度O(log2 n)
-
适用条件:采用顺序存储结构的有序表,不宜用于链式结构
分块查找(块间有序,块内无序)
- 分块有序,即分成若干子表,要求每个子表中的数值都比后一块中数值小(但子表内部未必有序)
- 然后将各子表中的最大关键字构成一个索引表,表中还要包含每个子表的起始地址(即头指针)。
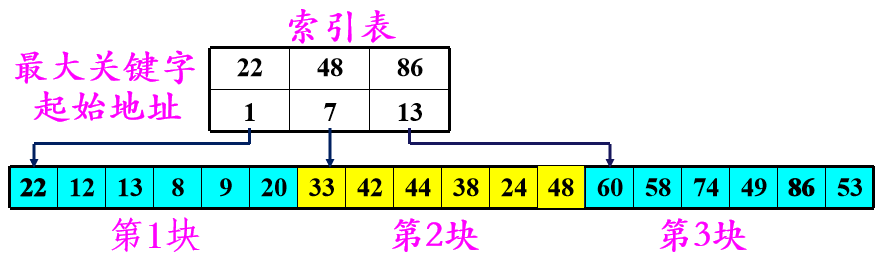
- 分块查找过程
- 对索引表使用折半查找法(因为索引表是有序表)
- 确定了待查关键字所在的子表后,在子表内采用顺序查找法(因为各子表内部是无序表
分块查找性能分析
- 查找效率:ASL = Lb + Lw
- Lb::对索引表查找的ASL
- Lw:对块内查找的ASL
- ASL(bs): = log2 (n/s+1)+s/2 (log2 n <= ASL(bs) <= n(n+1)/2)
- 例如,当n=9,s=3时,ASL(bs)=3.5, 而折半法为 3.1, 顺序法为 5
分块查找优缺点
- 优点:插入和删除比较容易,无需进行大量移动。
- 缺点:要增加一个索引表的存储空间并对初始索引表进行排序运算。
- 适用情况:如果线性表既要快速查找又经常动态变化,则可采用分块查找。
文章来源: ruochen.blog.csdn.net,作者:若尘,版权归原作者所有,如需转载,请联系作者。
原文链接:ruochen.blog.csdn.net/article/details/103530210
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者

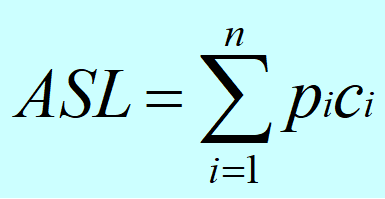

评论(0)