排序——快速排序
【摘要】
快速排序基本思想算法实现算法分析
快速排序
基本思想
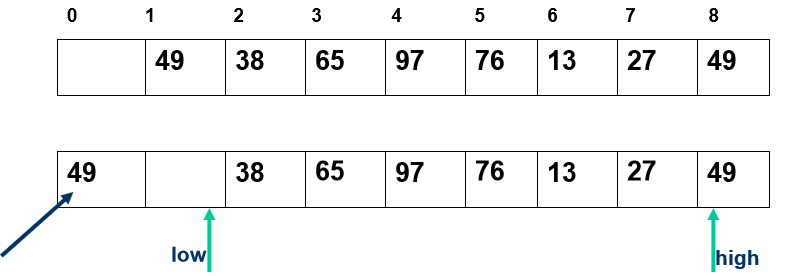
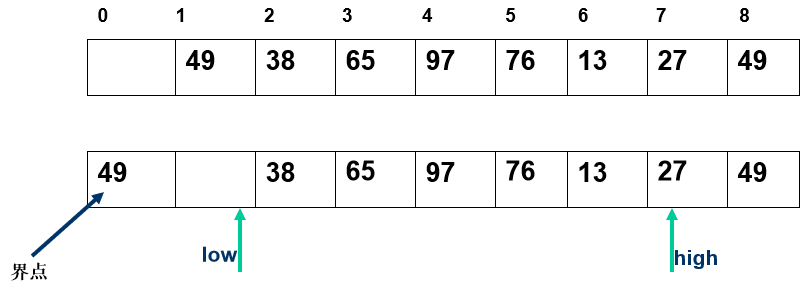
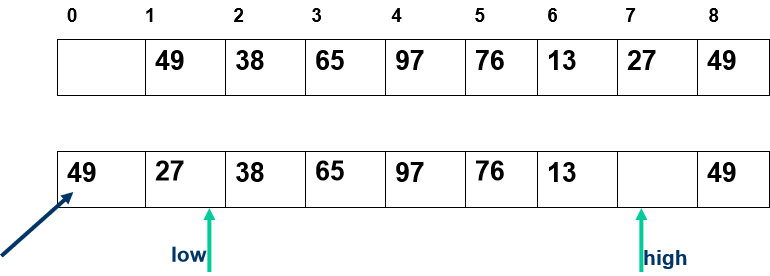
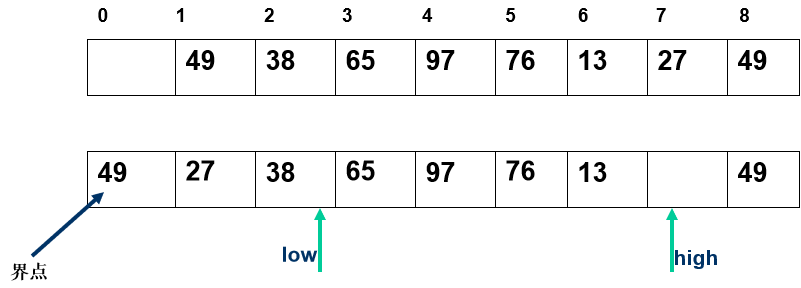
任取一个元素 (如第一个) 为中心所有比它小的元素一律前放,比它大的元素一律后放,形成左右两个子表;对各子表重新选择中心元素并依此规则调整,直到每个子表的元素只剩一个
算法实现
int Partition(SqList &L, int low, int...
快速排序
基本思想
- 任取一个元素 (如第一个) 为中心
- 所有比它小的元素一律前放,比它大的元素一律后放,形成左右两个子表;
- 对各子表重新选择中心元素并依此规则调整,直到每个子表的元素只剩一个
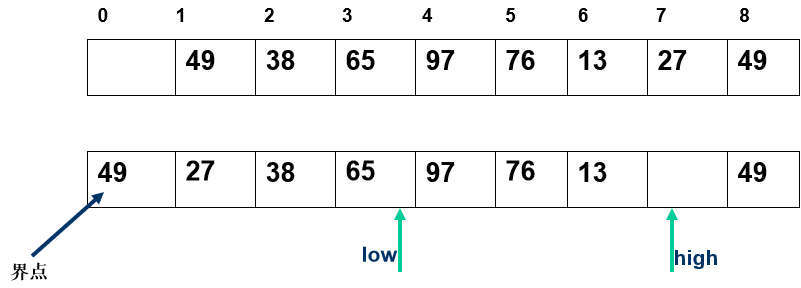
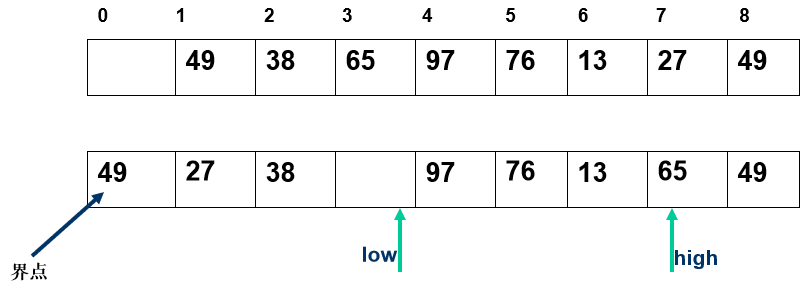
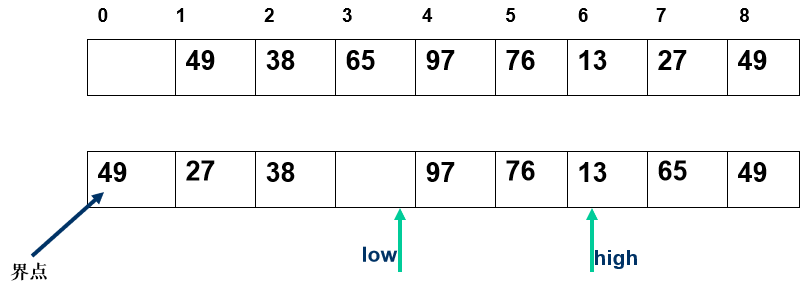
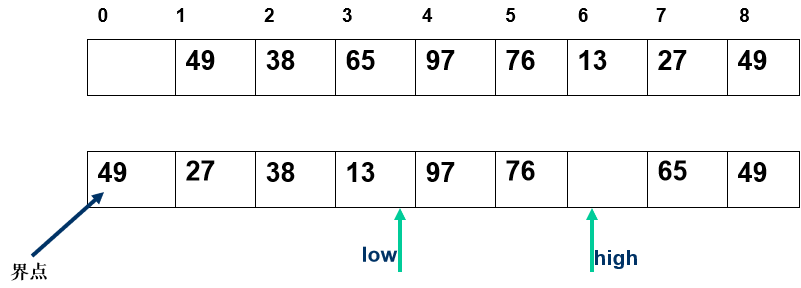
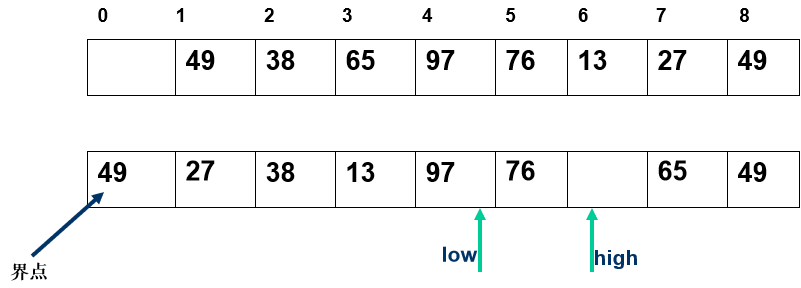
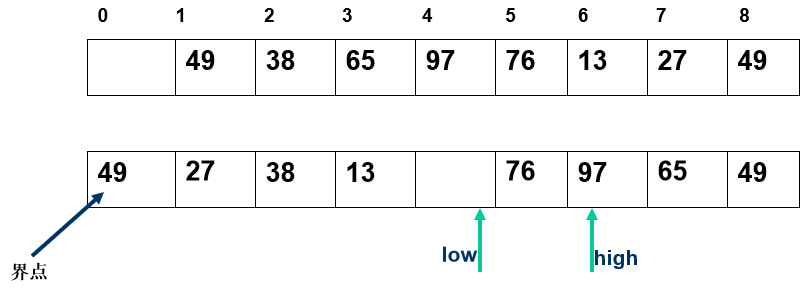
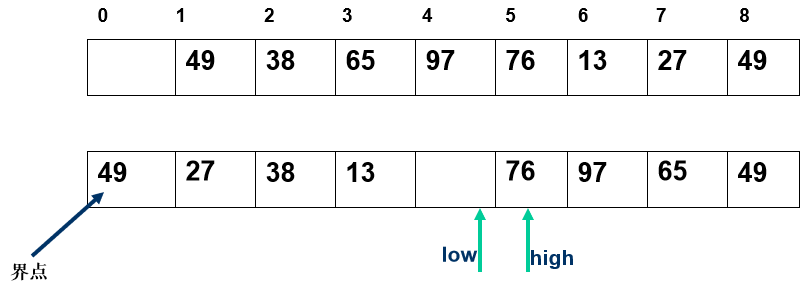
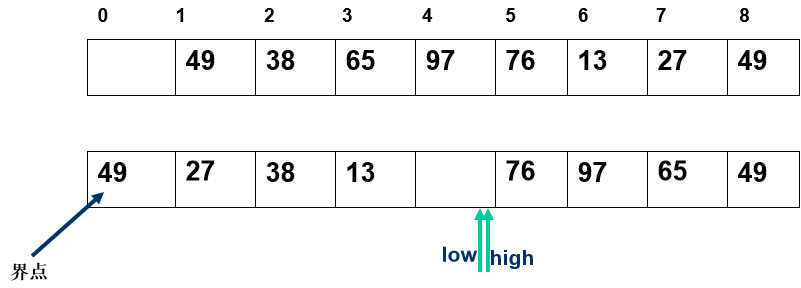
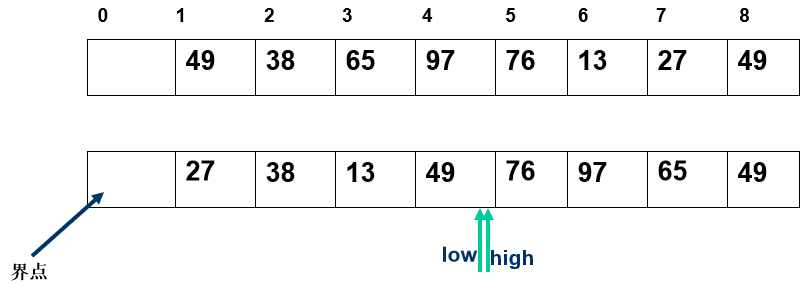
算法实现
int Partition(SqList &L, int low, int high){
L.r[0] = L.r[low];
pivotkey = L.r[low].key;
while(low < high){
while(low < high && L.r[high].key >= pivotkey) --high; // 从右向左搜索
L.r[low] = L.r[high];
while(low < high && L.r[low].key <= pivotkey) ++low; // 从左向右搜索
L.r[high] = L.r[low];
}
L.r[low] = L.r[0];
return low;
}
void QSort(SqList &L, int low, int high){
// 对记录序列L[low..high]进行快速排序
if(low < high){
// 长度大于1
pivotkey = Partition(L, low, high); // 对 L[low..high] 进行一次划分
QSort(L, low, pivotloc-1); // 对低子表递归排序,pivotloc是枢轴位置
QSort(L, pivotloc+1, high); // 对高子表递归排序
}
}
// 第一次调用函数 Qsort 时,待排序记录序列的上、下界分别为 1 和 L.length。
void QuickSort( SqList & L) {
// 对顺序表进行快速排序
QSort(L.r, 1, L.length);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
算法分析
- 时间复杂度:O(n^2)
- 最好: O(n log2n )
- 最坏:O(n^2)
- 平均:O(nlogn)
- 空间复杂度:O(n)
- O(log2n)—递归要用到栈空间
- 最坏情况下,递归树的高度为O(n)
- 稳定性:不稳定
文章来源: ruochen.blog.csdn.net,作者:若尘,版权归原作者所有,如需转载,请联系作者。
原文链接:ruochen.blog.csdn.net/article/details/103802754
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)