排序——插入排序
【摘要】
插入排序基本思想基本步骤:直接插入排序(基于顺序查找)算法描述算法实现算法分析时间复杂度 —— **O(n^2)**空间复杂度 —— O(1)稳定性 折半插入排序(基于折半查找)算法实现算法分析
插入排序
基本思想
每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。
即边插...
插入排序
基本思想
- 每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。
即边插入边排序,保证子序列中随时都是排好序的
基本步骤:
- 在R[1…i-1]中查找R[i]的插入位置;
R[1…j].key <= R[i].key < R[j+1…i-1].key - 将R[j+1…i-1]中的所有记录均后移一个位置;
- 将R[i] 插入(复制)到R[j+1]的位置上。
直接插入排序(基于顺序查找)
排序过程:整个排序过程为n-1趟插入,即先将序列中第1个记录看成是一个有序子序列,然后从第2个记录开始,逐个进行插入,直至整个序列有序。

算法描述
- 从R[i-1]向前进行顺序查找,监视哨设置在R[0]
- 关键字大于R[i].key的记录向后移动
if( L.r[i].key<L.r[i-1].key){
R[0] = R[i]; // 设置“哨兵”
R[i] = R[i-1];
for (j=i-2; R[0].key<R[j].key; --j)
R[j+1] = R[j]; - 循环结束表明R[i]的插入位置为 j+1
L.r[j+1]=L.r[0]; //插入到正确位置
算法实现
void InsertSort(SqList &L){
int i, j;
for(i = 2; i <= L.length; ++i){
if(L.r[i].key < L.r[i - 1].key){ // 将L.r[i]插入有序子表 L.r[0] = L.r[i]; // 复制为哨兵 L.r[i] = L.r[i - 1]; for(j = i - 2; L.r[0].key < L.r[j].key; --j) L.r[j + 1] = L.r[j]; // 记录后移 L.r[i + 1] = L.r[0]; // 插入到正确位置
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
算法分析
时间复杂度 —— O(n^2)
- 最好的情况(关键字正序)
- 比较次数:

- 移动次数:

- 比较次数:
- 最坏情况下(关键字逆序)
- 第 i 趟比较i次,移动i+1次
- 比较次数:

- 移动次数:

平均时间复杂度:O(n^2)
空间复杂度 —— O(1)
- 需要一个记录的辅助空间r(0)
稳定性
- 稳定
特点:简单、容易实现,适用于待排序记录基本有序或待排序记录较小时。
折半插入排序(基于折半查找)
基本思想:因为 R[1…i-1] 是一个按关键字有序的有序序列,则可以利用折半查找实现“在R[1…i-1]中查找R[i]的插入位置”,如此实现的插入排序为折半插入排序。
算法实现
void BiInsertionSort(SqList &L){
for(i = 2; i <= L.length; ++i){
L.r[0] = L.r[i]; // 将L.r[i] 暂存到 r[0]
// 在 L.r[1..i-1]中折半查找插入位置
low = 1;
high = i - 1;
while(low <= high){ m = (low + high) / 2; // 折半 if(L.r[0].key < L.r[m].key) high = m - 1; // 插入点在低半区 else low = m + 1; // 插入点在高半区
}
for(j = i - 1; j >= high + 1; --j) L.r[j + 1] = L.r[j];
L.r[high + 1] = L.r[0];
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
算法分析
- 时间复杂度为 O(n^2)
- 最佳情况下总时间代价为O(nlog2n)
- 最差和平均情况下仍为O(n^2)
- 空间复杂度为 O(1)
- 是一种稳定的排序方法
文章来源: ruochen.blog.csdn.net,作者:若尘,版权归原作者所有,如需转载,请联系作者。
原文链接:ruochen.blog.csdn.net/article/details/103802711
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者



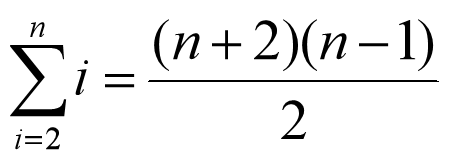
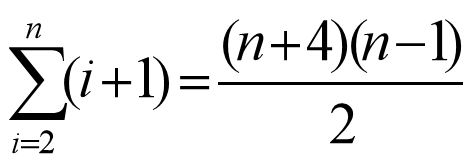

评论(0)