拓扑排序

AOE网

• 在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，边上的权值表示活动的持续时间，称这样的有向图叫做边表示活动的网，简称AOE网。AOE网中没有入边的顶点称为始点（或源点），没有出边的顶点称为终点（或汇点）。

AOE网的性质

• 只有在某顶点所代表的事件发生后，从该顶点出发的各活动才能开始；
• 只有在进入某顶点的各活动都结束，该顶点所代表的事件才能发生。

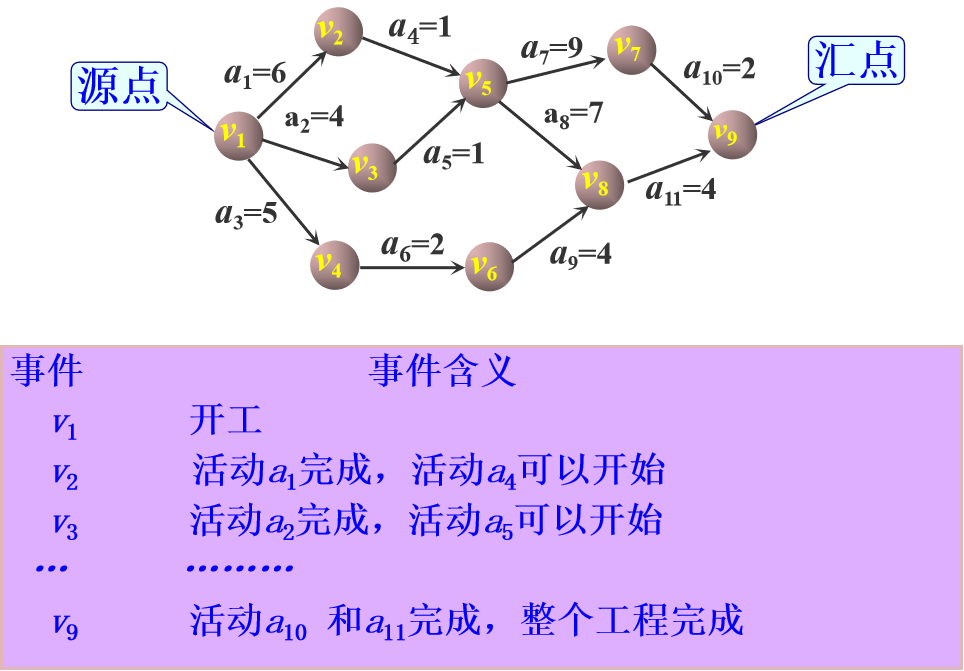
AOE网所能解决的问题

• 完成整个工程至少需要多少时间?
• 为缩短完成工程所需的时间, 应当加快哪些活动?

关键路径

关键路径长度是整个工程所需的最短工期。

• 关键路径：在AOE网中，从始点到终点具有最大路径长度（该路径上的各个活动所持续的时间之和）的路径称为关键路径。
• 关键活动：关键路径上的活动称为关键活动。

术语

• 源点：表示整个工程的开始点，也称起点
• 收点：表示整个工程的结束点，也称汇点
• 事件结点：单位时间，表示的是时刻
• 活动（有向边）：它的权值定义为活动进行所需要的时间。方向表示起始结点事件先发生，而终止结点事件才能发生
• 事件的最早发生时间（Ve(j)）：从起点到本结点的最长的路径。意味着事件最早能够发生的时刻
• 事件的最迟发生时间（V l (j)）：不影响工程的如期完工，本结点事件必须发发生的时刻
• 活动的最早开始时间：e( ai ) = Ve( j )
• 活动的最迟开始时间：l( ai ) = V l( k ) - dut( j , k )
• 事件的最早发生时间（Ve(j)）：从起点到本结点的最长的路径。意味着事件最早能够发生的时刻
• 事件的最迟发生时间（V l (j)）：不影响工程的如期完工，本结点事件必须发发生的时刻
• 活动的最早开始时间：e(ai ) = Ve( j )
• 活动的最迟开始时间： l (ai ) = V l( k ) - dut( j , k )
• 关键活动：最早开始时间 ＝ 最迟开始时间的活动
• 关键路径：从源点到收点的最长的一条路径，或者全部由关键活动构成的路径

算法设计

• 事件(顶点) 的 最早发生时间 ve(j)
  ve(j) = 从源点到顶点j的最长路径长度

  • ve(源点) = 0
  • ve(j) = Max{ve(i) + dut(<i, j>)} (<i, j>∈T)
    T是所有以第j个顶点为弧头的弧的集合

• 事件(顶点) 的 最迟发生时间 vl(k)
  vl(k) = 从顶点k到汇点的最短路径长度

  • vl(汇点) = ve(汇点)
  • vl(i) = Min{vl(j) – dut(<i, j>)} (<i, j>∈S)
    S是所有以第i个顶点为弧尾的弧的集合

假设第 i 条弧为 <j, k>, 则 对第 i 项活动言:

• 活动(弧)”的 最早开始时间 e(i)
  e(i) = ve(j)
• 活动(弧)的 最迟开始时间 l(i)
  l(i) = vl(k) – dut(<j,k>)

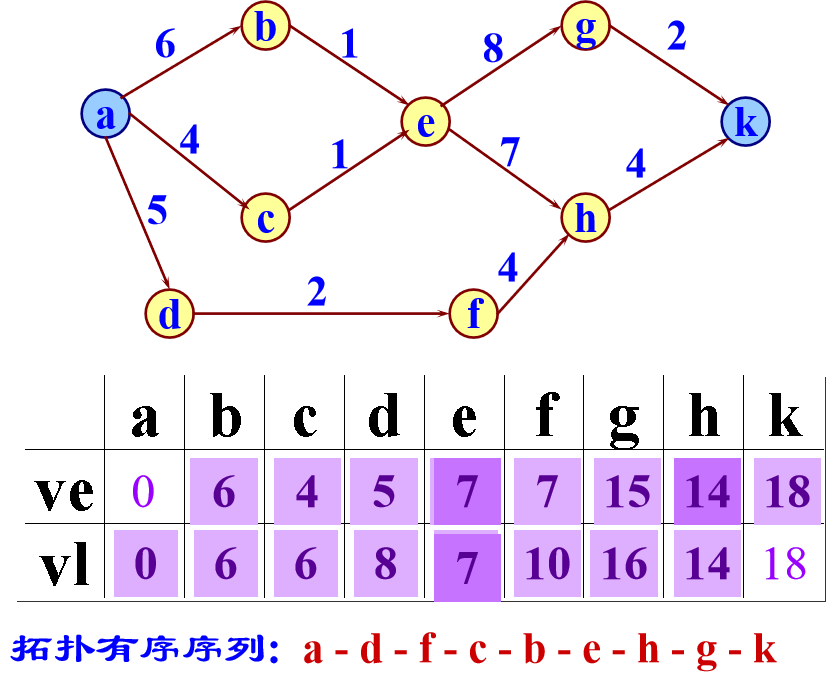
算法要点

• 求ve的顺序应该是按拓扑有序的次序
• 求vl的顺序应该是按拓扑逆序的次序
• 拓扑逆序序列即为拓扑有序序列的逆序列，应该在拓扑排序的过程中，另设一个 “栈” 记下拓扑有序序列

算法实现

Status TopologicalOrder(ALGraph G, SqStack &T){
	FindInDegree(G, indegree);  // 对各顶点求入度
	InitStack(S);
	InitStack(T);
	for(i = 0; i < G.vexnum; i++)
		if(!indegree[i]) Push(S, i);
	count = 0;  // 对输出顶点计数
	for(i = 0; i < G.vexnum; i++)
		ve[i] = 0;
	while(!StackEmpty(S)){
		Pop(S, j);
		Push(T, j);
		++count;
		for(p = G.vertices[j].firstarc; p; p = p->nextarc){ k = p->adjvex; if(!(--indegree[k])) Push(S, k); if(ve[j] + *(p->info) > ve[k]) // 修改ve[j] ve[k] = ve[j] + *(p->info);
		}
	}
	if(count < G.vexnum){
		cout << "图中有回路!";
		return ERROR;
	}
}

void Criticalpath(ALGraph G){
	// G为有向网络，输出G的各项关键活动
	for(i = 0; i < G.vexnum; i++)
		vl[i] = ve[G.vexnum - 1]
	while(!StackEmpty(T))
		for(Pop(T, j), p = G.vertices[j].firstarc; p; p = p->nextarc){ k = p->adjvex; dut = *(p->info); if(vl[k] - dut < vl[j]) vl[j] = vl[k] - dut; // dut是事件vj到事件vk活动的持续时间
		}
	for(j = 0; j < G.vexnum; ++j){
		// 求活动的最早开始时间ee、最迟开始时间el和关键活动
		for(p = G.vertices[j].firstarc; p; p = p->nextarc){ k = p->adjvex; dut = *(p->info); ee = ve[j]; el = vl[k] - dut; tag = (ee == el)?'*':' '; cout << j << " " << k << " " << dut <<" " << ee << " " << el << " " << tag << endl;
		}
	}
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
 

文章来源: ruochen.blog.csdn.net，作者：若尘，版权归原作者所有，如需转载，请联系作者。

原文链接：ruochen.blog.csdn.net/article/details/103977540