Py之cvxopt：cvxopt库的简介、安装、使用方法之详细攻略

目录

cvxopt库的简介

cvxopt库的安装

cvxopt库的使用方法

1、创建矩阵

2、求解线性规划

cvxopt库的简介

       CVXOPT是一个基于Python编程语言的凸优化的免费软件包。它可以与交互式Python解释器一起使用，也可以通过执行Python脚本在命令行上使用，或者通过Python扩展模块集成到其他软件中。它的主要目的是通过构建Python的广泛标准库和Python作为一种高级编程语言的优势，使凸优化应用程序的软件开发变得简单。

官网：http://cvxopt.org/

cvxopt库的安装

pip install cvxopt

cvxopt库的使用方法

1、创建矩阵

CVXOPT有单独的稠密和稀疏矩阵对象。这个例子演示了创建密集和稀疏矩阵的不同方法。使用matrix()函数创建一个密集矩阵;它可以通过列表(或迭代器)创建:

  

   

    

     

    
    

     

      >>> from cvxopt import matrix
     
    
   

    

     

    
    

     

      >>> A = matrix([1.0, 2.0, 3.0, 4.0, 5.0, 6.0], (2,3))
     
    
   

    

     

    
    

     

      >>> print(A)
     
    
   

    

     

    
    

     

      [ 1.00e+00  3.00e+00  5.00e+00]
     
    
   

    

     

    
    

     

      [ 2.00e+00  4.00e+00  6.00e+00]
     
    
   

    

     

    
    

     

      >>> A.size
     
    
   

    

     

    
    

     

      (2, 3)
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      >>> B = matrix([ [1.0, 2.0], [3.0, 4.0] ])
     
    
   

    

     

    
    

     

      >>> print(B)
     
    
   

    

     

    
    

     

      [ 1.00e+00  3.00e+00]
     
    
   

    

     

    
    

     

      [ 2.00e+00  4.00e+00]
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      >>> print(matrix([ [A] ,[B] ]))
     
    
   

    

     

    
    

     

      [ 1.00e+00  3.00e+00  5.00e+00  1.00e+00  3.00e+00]
     
    
   

    

     

    
    

     

      [ 2.00e+00  4.00e+00  6.00e+00  2.00e+00  4.00e+00]
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      >>> from cvxopt import spmatrix
     
    
   

    

     

    
    

     

      >>> D = spmatrix([1., 2.], [0, 1], [0, 1], (4,2))
     
    
   

    

     

    
    

     

      >>> print(D)
     
    
   

    

     

    
    

     

      [ 1.00e+00 0 ]
     
    
   

    

     

    
    

     

      [ 0 2.00e+00]
     
    
   

    

     

    
    

     

      [ 0 0 ]
     
    
   

    

     

    
    

     

      [ 0 0 ]
     
    
   

    

     

    
    

     

      >>> print(matrix(D))
     
    
   

    

     

    
    

     

      [ 1.00e+00  0.00e+00]
     
    
   

    

     

    
    

     

      [ 0.00e+00  2.00e+00]
     
    
   

    

     

    
    

     

      [ 0.00e+00  0.00e+00]
     
    
   

    

     

    
    

     

      [ 0.00e+00  0.00e+00]
     
    
   

    

     

    
    

     
 
     
    
  
 

2、求解线性规划

可以通过求解器.lp()函数指定线性程序

  

   

    

     

    
    

     

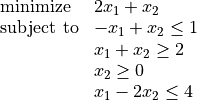
      >>> from cvxopt import matrix, solvers
     
    
   

    

     

    
    

     

      >>> A = matrix([ [-1.0, -1.0, 0.0, 1.0], [1.0, -1.0, -1.0, -2.0] ])
     
    
   

    

     

    
    

     

      >>> b = matrix([ 1.0, -2.0, 0.0, 4.0 ])
     
    
   

    

     

    
    

     

      >>> c = matrix([ 2.0, 1.0 ])
     
    
   

    

     

    
    

     

      >>> sol=solvers.lp(c,A,b)
     
    
   

    

     

    
    

     

       pcost dcost gap pres   dres   k/t
     
    
   

    

     

    
    

     
 0:  2.6471e+00 -7.0588e-01  2e+01  8e-01  2e+00  1e+00
     
    
   

    

     

    
    

     
 1:  3.0726e+00  2.8437e+00  1e+00  1e-01  2e-01  3e-01
     
    
   

    

     

    
    

     
 2:  2.4891e+00  2.4808e+00  1e-01  1e-02  2e-02  5e-02
     
    
   

    

     

    
    

     
 3:  2.4999e+00  2.4998e+00  1e-03  1e-04  2e-04  5e-04
     
    
   

    

     

    
    

     
 4:  2.5000e+00  2.5000e+00  1e-05  1e-06  2e-06  5e-06
     
    
   

    

     

    
    

     
 5:  2.5000e+00  2.5000e+00  1e-07  1e-08  2e-08  5e-08
     
    
   

    

     

    
    

     

      >>> print(sol['x'])
     
    
   

    

     

    
    

     

      [ 5.00e-01]
     
    
   

    

     

    
    

     

      [ 1.50e+00]
     
    
  
 

文章来源: yunyaniu.blog.csdn.net，作者：一个处女座的程序猿，版权归原作者所有，如需转载，请联系作者。

原文链接：yunyaniu.blog.csdn.net/article/details/111026294