分治(详解残缺棋盘 —— Java代码实现)
【摘要】
分治总体思想使用条件基本步骤案例覆盖残缺棋盘大整数的乘法Strassen矩阵乘法
分治
总体思想
将要求解的较大规模的问题分割成k个更小规模的子问题对这k个子问题分别求解。如果子问题的规模仍然不够小,则再划分为k为子问题,如此递归进行下去,直到问题规模足够小,很容易求出其解为止将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上...
分治
总体思想
- 将要求解的较大规模的问题分割成k个更小规模的子问题
- 对这k个子问题分别求解。如果子问题的规模仍然不够小,则再划分为k为子问题,如此递归进行下去,直到问题规模足够小,很容易求出其解为止
- 将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上逐步求出原来的问题的解
使用条件
- 该问题的规模缩小到一定的程度就可以容易地解决
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质
- 利用该问题分解出的子问题的解可以合并为该问题的解
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题
能否利用分治法完全取决于子问题是否具有这条特征,如果具备了前两条特征,而不具备第三条特征,则可以考虑贪心算法或动态规划
基本步骤
divide-and-conquer(P) {
if (|P| <= n0) abhoc(P); // 解决小规模的问题
divide P into smaller subinstances P1, P2 ,... ,Pk // 分解问题
for (i = 1; i <= k; i++) {
yi = divide-and-conquer(Pi); // 递归的解各子问题
return merge(y1, ... ,yk) // 将各子问题的解合并为原问题的解
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
案例
覆盖残缺棋盘
- 在一个2k×2k 个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。
- 用 (n2) / 3个三重格放置在 n × n 的缺陷棋盘上,正好能够覆盖所有方格

具体步骤:

-
划分为四个小棋盘
-
其中一个是 4 × 4 缺陷棋盘

-
在其他三个 4 × 4 棋盘都都相邻的拐角上放一个三格板,使它们也成为缺陷棋盘
-
递归地覆盖四个4×4缺陷棋盘
-
在其它三个 4 × 4 棋盘都相邻的拐角上放一个三格板,使它们也成为缺陷棋盘。

Java代码实现
package Chess;
public class Chess {
// 表示棋盘
private int[][] board;
// 表示棋盘的大小为2的多少次方
private int boardSize;
// 棋盘中特殊方格的位置(行号,列号)
private int dr, dc;
private int tile = 1; public Chess() {
board = new int[1][1];
dr = 0;
dc = 0;
boardSize = 0;
} public Chess(int r, int c, int s) {
int n;
n = (int) Math.pow(2, s);
if (n <= r || n <= c) System.out.println("初始化参数错误!");
else { board = new int[n][n]; dr = r; dc = c; boardSize = s;
}
} public void Print() {
for (int i = 0; i < Math.pow(2, this.boardSize); i++) { for (int j = 0; j < Math.pow(2, this.boardSize); j++) { System.out.printf("%3d|", this.board[i][j]); } System.out.println();
}
} public static void main(String[] args) {
// 2^2*2^2棋盘, 假设特殊方格位置为(3, 3)
Chess c1 = new Chess(3, 3, 2);
c1.chessBoard(0, 0, c1.dr, c1.dc, (int)Math.pow(2, c1.boardSize));
c1.Print();
} /**
* @param tr:棋盘左上角方格的行号
* @param tc:棋盘左上角方格的列号
* @param dr:特殊方格所在的行号
* @param dc:特殊棋盘所在的列号
* @param size:2^k, 棋盘的规格为 2^k*2^k
**/
public void chessBoard(int tr, int tc, int dr, int dc, int size) {
if (size == 1) return; // t: L型骨牌号,s分割棋盘
int t = tile++;
int s = size / 2; // 覆盖左上角棋盘
if (dr < tr + s && dc < tc + s) { // 特殊方格在此棋盘中 chessBoard(tr, tc, dr, dc, s);
} else { // 此棋盘中无特殊方格则用t号L型骨牌覆盖右下角 board[tr + s - 1][tc + s - 1] = t; // 覆盖其余方格 chessBoard(tr, tc, tr + s - 1, tc + s - 1, s);
} // 覆盖右上角子棋盘
if (dr < tr + s && dc >= tc + s) { // 特殊方格在此棋盘中 chessBoard(tr, tc + s, dr, dc, s);
} else { // 无特殊方格,用t号骨牌覆盖左下角 board[tr + s - 1][tc + s] = t; chessBoard(tr, tc + s, tr + s - 1, tc + s, s);
} // 覆盖左下角棋盘
if (dr >= tr + s && dc < tc + s) { chessBoard(tr + s, tc, dr, dc, s);
} else { // 无特殊方格,用t号骨牌覆盖右上角 board[tr + s][tc + s - 1] = t; chessBoard(tr + s, tc, tr + s, tc + s - 1, s);
} // 覆盖右下角棋盘
if (dr >= tr + s && dc >= tc + s) { // 特殊方格在此棋盘中 chessBoard(tr + s, tc + s, dr, dc, s);
} else { // 无特殊方格,用t号骨牌覆盖左上角 board[tr + s][tc + s] = t; chessBoard(tr + s, tc + s, tr + s, tc + s, s);
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
2| 2| 3| 3|
2| 1| 1| 3|
4| 1| 5| 5|
4| 4| 5| 0|
- 1
- 2
- 3
- 4
大整数的乘法
- 小学的方法:效率太低 O(n2)
- 分治法:

X = A × 2n/2 + B
Y = C × 2n/2 + D
XY = (A × 2n/2 + B)(C × 2n/2 + D)
=AC × 2n + (AD + CB) × 2n/2 + BD

实质上没有改进
再次进行改进:
XY = AC × 2n + (AD + CB) × 2n/2 + BD
=AC × 2n + ((A - B)(D - C) + AC + BD) × 2n/2 + BD
这样只需进行3次 n/2 位乘法

T(n) = O(nlog3) = O(n1.59) (有了较大的改进)
如果将大整数分成更多段,用更复杂的方式把它们组合起来,将有可能得到更优的算法
Strassen矩阵乘法

易知,时间复杂度为 O(n3)
分治法:
-
将矩阵A、B和C中每一矩阵都分成4个大小相等的子矩阵,则 C = AB 可写为:

由此可得:


实际复杂度还是没有变,仍然为 O(n3) -
为了降低时间复杂度,要减少乘法的次数

这样,复杂度得到了改进

文章来源: ruochen.blog.csdn.net,作者:若尘,版权归原作者所有,如需转载,请联系作者。
原文链接:ruochen.blog.csdn.net/article/details/104863703
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者





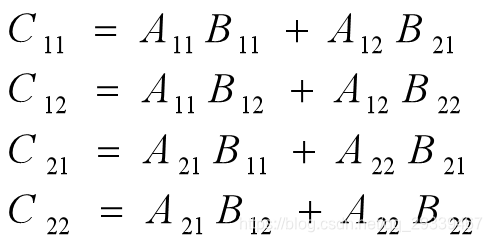
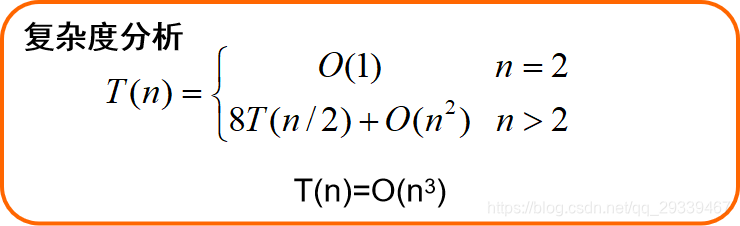
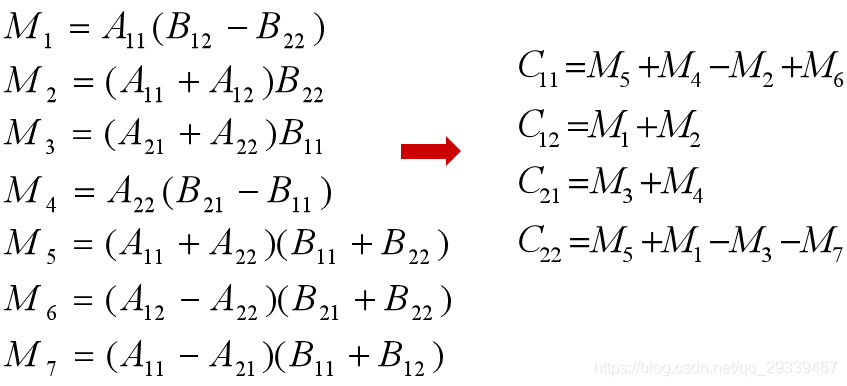
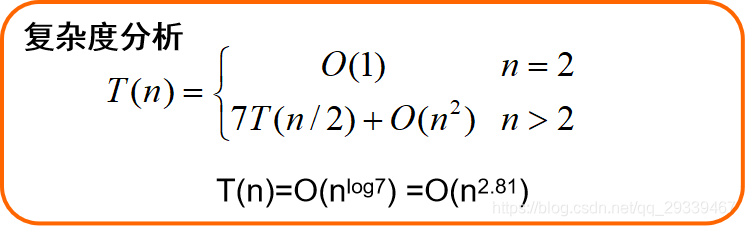

评论(0)