归并排序

归并排序

归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

什么是的分治（divide-and-conquer）策略：

分解：把一个问题分解成多个子问题，这些子问题是更小实例上的原问题。
解决：递归地求解子问题，当子问题足够小时，按照基础情况来求解。
合并：把子问题的解合并成原问题的解。

下面是归并排序，采用分治法的过程图，下面将对每个过程做详细说明。

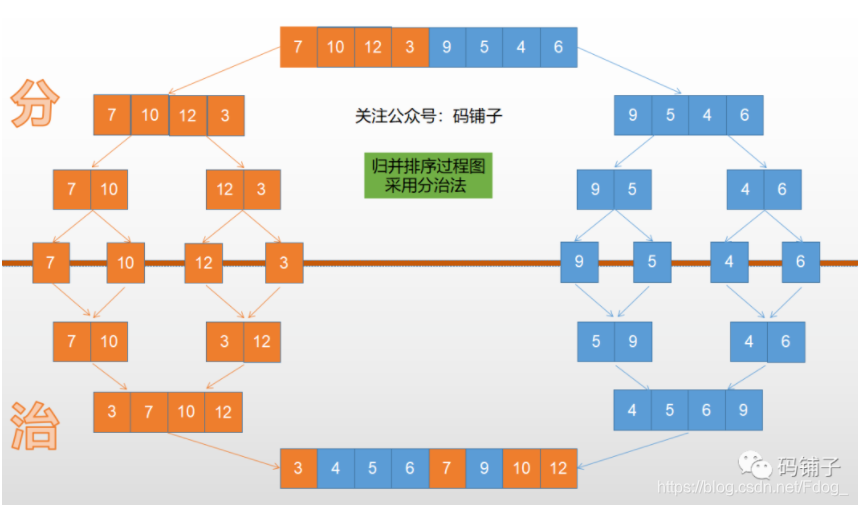
下面使用递归对数组进行了递归分解，直到startIndex < endIndex条件不成立，才进行合并，当然，在合并之前，应完成排序，但目前我们不考虑排序，只需要看懂如何分解即可。

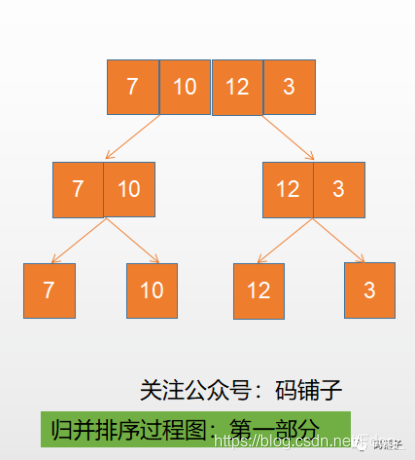
下面是排序示意图

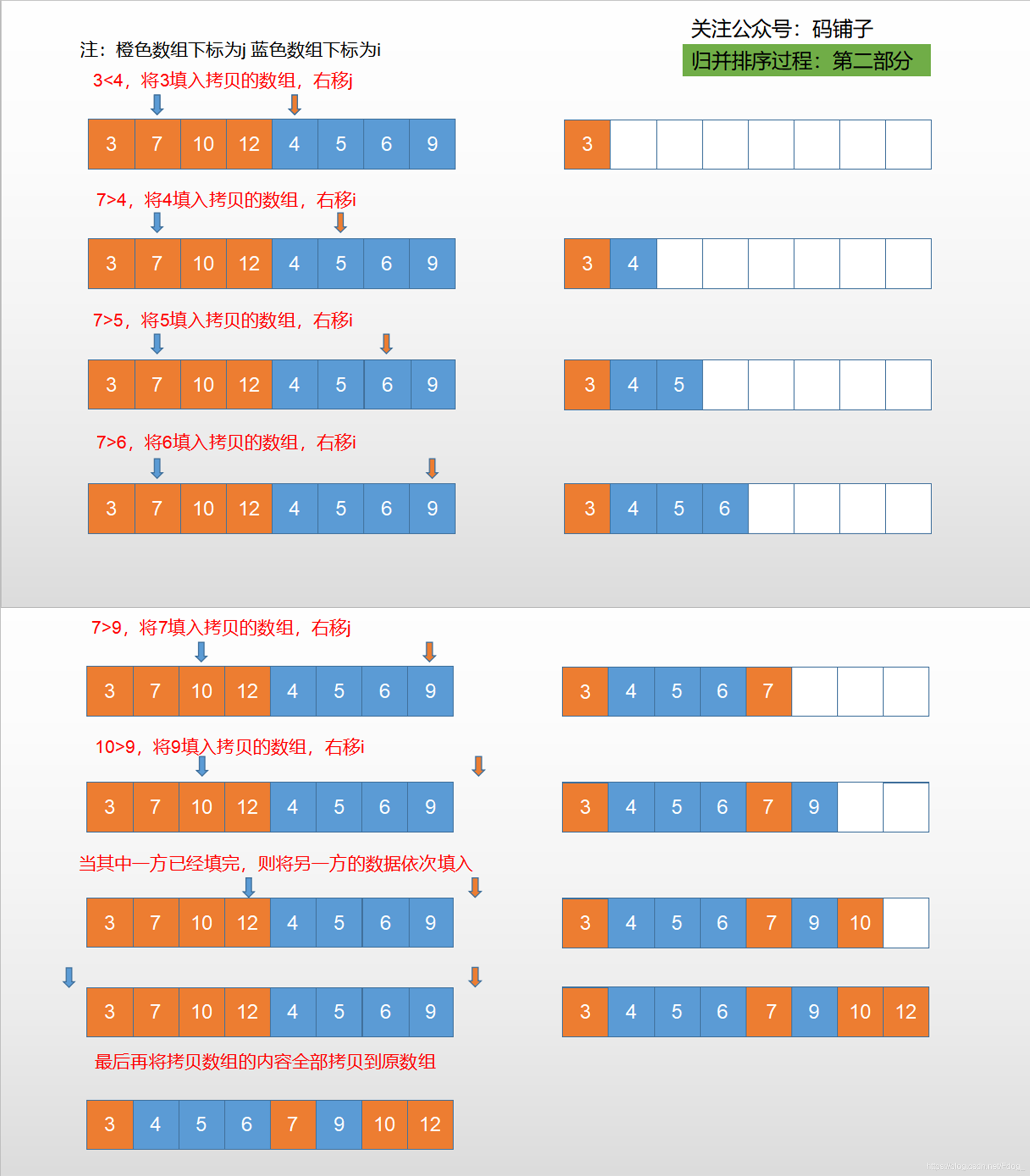
归并操作的工作原理

归并操作的工作原理如下：

[1]申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列。
[2]设定两个指针，最初位置分别为两个已经排序序列的起始位置
[3]比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
[4]重复步骤3直到某一指针超出序列尾
[5]将另一序列剩下的所有元素直接复制到合并序列尾

注意：归并排序不是原址的，它必须将整个输入数组进行完全的拷贝，而前面说过的冒泡排序，选择排序，或者是插入排序，在任何时间都是不拷贝或者只拷贝一个数组项，而不是对整个数组的拷贝。

代码

void MergeSort(int * arr, int * arr_copy,int s,int n)
{
	int min;
	if (s < n)
	{
		min = s+(n-s) / 2;
		//不要写成n/2
		MergeSort(arr, arr_copy, s, min);
		MergeSort(arr, arr_copy, min + 1, n);
		int i = s, j = min + 1, k = s;
		while (i != min + 1 && j != n + 1)
		{ if (arr[i] > arr[j]) arr_copy[k++] = arr[j++]; else arr_copy[k++] = arr[i++];
		}
		while (i != min + 1)
		{ arr_copy[k++] = arr[i++];
		}
		while (j != n + 1)
		{ arr_copy[k++] = arr[j++];
		}
		for (i = s; i <= n; i++)
		{ arr[i] = arr_copy[i]; cout << "arr" << i << "是" << arr[i]<<endl;
		}
		cout << endl;
	}
}
int main()
{
	int arr[] = { 1,5,69,8,10,6 };
	int arr_copy[6] = { 0 };
	//将数组分解,排序 
	//原数组，复制数组 数组长度
	MergeSort(arr, arr_copy,0,5);
	return 0;
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
 

文章来源: blog.csdn.net，作者：花狗Fdog，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/Fdog_/article/details/113782371