为实习准备的数据结构(9)-- 跳表
跳表
让你现场手写一棵红黑树、AVL树、伸展树之类的,你行吗?
要不让我查资料,我估计只能扯皮。
跳表就不一样了,看懂它的原理很简单,根据它的原理直接手写也是可以实现的。
为什么?
跳表(skip list) 对应的是平衡树(AVL Tree),是一种 插入/删除/搜索 都是 O(log n) 的数据结构。它最大的优势是原理简单、容易实现、方便扩展、效率更高。因此在一些热门的项目里用来替代平衡树,如 redis, leveldb 等。
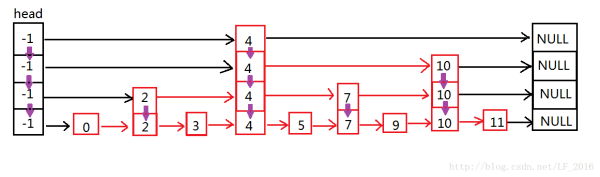
跳表是一个随机化的数据结构,实质就是一种可以进行二分查找的有序链表。跳表在原有的有序链表上面增加了多级索引,通过索引来实现快速查找。
链表会写不?链表不会写的话,可以走了。
开头那张图看着有感觉吗?我第一眼看到那个图,大概就明白了,同时觉得,秀啊!!!
还能这么玩。
一个节点要不要被索引,建几层的索引,都在节点插入时由抛硬币决定。当然,虽然索引的节点、索引的层数是随机的,为了保证搜索的效率,要大致保证每层的节点数目与上节的结构相当(差不多对半开)。

跳表的搜索

我现在要在这里面搜索“17”,具体流程是如何的呢?
为了加快搜索,需要从最高层4开始搜索(因为最高层的节点少,容易定位),首先查看6节点,发现17比其大,向后搜索,发现6后面的节点指向了Nil(第4层),那么搜索的层数降低1层,
从此节点的第3层开始搜索,发现下个节点是25,大于17,那么再降低一层,从2层开始搜索,发现第2层是9,小于17,继续搜索,发现9节点的下一个数是17,搜索完成。总共查询了
4次,完成搜索(不包含Nil节点的访问。),这种情况下普通有序链表需要6次访问。可以设想下,如果层数为1层的话,那么此时跳表为最坏的情况,退化成有序单链表。复杂度O(n)。
- 1
- 2
- 3
- 4
- 5
跳表的插入
第一步:找到待插入节点该去的位置。
第二步:确定该元素要占据的层数 K(采用丢硬币的方式,这完全是随机的)。
第三步:在 Level 1 … Level K 各个层的链表都插入元素。
第四步:用Update数组记录插入位置,同样从顶层开始,逐层找到每层需要插入的位置,再生成层数并插入。
(这个update数组不知道的话先存疑)
抛硬币
抛硬币,如果是正面(random() < p)则层数加一,直到抛出反面为止。设置一个 MaxLevel,防止如果运气太好,层数就会太高,而太高的层数往往并不会提供额外的性能。
跳表的删除
删除的时候和插入相同,都是先搜索。唯一注意的一点是删除的节点也许要修改skiplist->length的值。
销毁整个调表的时候,从level=1销毁即可,别忘记释放head和skiplist。
这里就不过多的放图了,意会一下子。
大年初一还要搞代码,哎。
跳表的代码实现
跳表数据结构
如上图中的E节点,表示的是头节点,一般跳表的实现,最大有多少层(MAX_LEVEL)是确定的。所以e的个数是固定的。
#define SKIPLIST_MAXLEVEL 32
#define ZSKIPLIST_P 0.25
typedef struct skiplistNode_t{ void* value; double score; struct skiplistNode_t* forward[];
}skiplistNode;
typedef struct skiplist{ skiplistNode* head; int level; uint32_t length;
}skiplist;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
初始化跳表
skiplistNode* createNode(int level,void* value,double score)
{ skiplistNode *slNode = (skiplistNode*)malloc(sizeof(*slNode)+level*sizeof(skiplistNode)); if(!slNode) { return NULL; } slNode->value = value; slNode->score = score; return slNode;
}
skiplist* slCreate(void)
{ int i; skiplist* sl = (skiplist*)malloc(sizeof(*sl)); if(!sl) { return NULL; } sl->length = 0; sl->level = 1; sl->tail = NULL; sl->head = createNode(SKIPLIST_MAXLEVEL,NULL,0.0); for(i=0;i<SKIPLIST_MAXLEVEL;i++) { sl->head->forward[i] = NULL; } return sl;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
插入节点
插入的时候,会调用一个randomLevel的函数,他可以概率返回1~MAX_LEVEL之间的值,但是level的值越大,概率越小。
skiplistNode *slInsert(skiplist *sl, void* value, double score)
{ skiplistNode* sn,*update[SKIPLIST_MAXLEVEL]; int i, level; sn = sl->head; for(i=sl->level-1;i>=0;i--) { while(sn->forward[i]&&(sn->forward[i]->score<score)){ sn = sn->forward[i]; } update[i] = sn; } if(sn->forward[0]&&sn->forward[0]->score == score) { printf("insert failed,exist!!\n"); return NULL; } level = slRandomLevel(); printf("score:%.2lf level:%d\n",score,level); if(level>sl->level){ for(i=sl->level;i<level;i++) { update[i] = sl->head; } sl->level = level; } sn = createNode(level,value,score); for(i=0;i<level;i++) { sn->forward[i] = update[i]->forward[i]; update[i]->forward[i] = sn; } sl->length++; return sn;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
删除节点
int slDelete(skiplist *sl, double score)
{ skiplistNode *update[SKIPLIST_MAXLEVEL]; skiplistNode *sn; int i; sn = sl->head; for(i=sl->level-1;i>=0;i--) { while(sn->forward[i]&&sn->forward[i]->score<score){ sn = sn->forward[i]; } update[i] = sn; } sn = sn->forward[0]; if(sn->score != score) { return -1; } for(i=0;i<sl->level;i++) { if(update[i]->forward[i] != sn){ break; } update[i]->forward[i] = sn->forward[i]; } free(sn); while(sl->level>1&&sl->head->forward[sl->level-1] == NULL){ sl->level--; } sl->length--; return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
销毁跳表
销毁整个调表的时候,从level=1销毁即可,别忘记释放head和skiplist。
void slFree(skiplist *sl)
{ skiplistNode* sn = sl->head,*st; st = sn->forward[0]; free(sn); while(st) { sn = st->forward[0]; free(st); st = sn; } free(sl);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
接下来我们看点其它的,碧如说跳表与redis。(我第一次接触跳表也是在redis的源码中)
为什么Redis要用跳表来实现有序集合?
性能. 主要是对标AVL. 但是AVL实现复杂,对于频繁的增删操作极大可能造成子树的平衡操作,这样很明显就会浪费性能。
请看开发者说的,他为什么选用skiplist The Skip list:
There are a few reasons:1) They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.2) A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.3) They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.About the Append Only durability & speed, I don’t think it is a good idea to optimize Redis at cost of more code and more complexity for a use case that IMHO should be rare for the Redis target (fsync() at every command). Almost no one is using this feature even with ACID SQL databases, as the performance hint is big anyway.About threads: our experience shows that Redis is mostly I/O bound. I’m using threads to serve things from Virtual Memory. The long term solution to exploit all the cores, assuming your link is so fast that you can saturate a single core, is running multiple instances of Redis (no locks, almost fully scalable linearly with number of cores), and using the “Redis Cluster” solution that I plan to develop in the future.
在并发环境下skiplist有另外一个优势,红黑树在插入和删除的时候可能需要做一些rebalance的操作,这样的操作可能会涉及到整个树的其他部分,而skiplist的操作显然更加局部性一些,锁需要盯住的节点更少,因此在这样的情况下性能好一些。
大过年的,祝大家新年快乐哦!!!


文章来源: lion-wu.blog.csdn.net,作者:看,未来,版权归原作者所有,如需转载,请联系作者。
原文链接:lion-wu.blog.csdn.net/article/details/113794615
- 点赞
- 收藏
- 关注作者


评论(0)